Fehler als Lerngelegenheiten – eine kompetenzorientierte Sichtweise
Fehler zu machen gehört zum Lernen dazu – so auch im Mathematikunterricht der Grundschule. Diese Fehler spiegeln den aktuellen Wissensstand der Kinder wider und sollten deshalb nicht nur als Hürden, sondern ebenso und insbesondere als Lerngelegenheiten im Unterricht „erlebt“ und „genutzt“ werden.
Stärkenorientierung – Fehler gehören zum Lernen dazu
Die bestmögliche Förderung aller Kinder sollte das Ziel eines jeden Unterrichts sein. Dafür sollte man im Unterrichtsgeschehen nicht nur die Fehler oder Schwierigkeiten im Blick haben, die die Kinder machen. Denn die Kinder machen oftmals zugleich auch vieles richtig, auf das man im weiteren Unterrichtsverlauf aufbauen kann, sodass die Kinder eine zielgerichtete Förderung erhalten können.
Um die Kinder gezielt fördern zu können, sodass diese ihre Fehler überwinden können, müssen zunächst mit Hilfe des kompetenzorientierten Blicks die Ursachen der Schwierigkeiten und Fehler erkannt werden (vgl. Sundermann & Selter 2006, S.13 f.).
Am Beispiel von Melissa soll dies im Folgenden verdeutlicht werden:
Melissa (siehe Schülerdokument und Video) rechnet die Aufgabe 46-28, indem sie zunächst stellenweise die Zehner 40-20 und dann die Einer verrechnet. Hier fällt bei den Zehnern auf, dass sie statt einem Minus ein Pluszeichen verwendet. Bei den Einern behilft sich Melissa, indem sie 6-8 vertauscht und die kleinere Zahl von der größeren Zahl abzieht, sie rechnet also 8-6.
Warum vertauscht Melissa die Einer? Die Kinder haben bei der Addition gelernt, dass ein vertauschen der Summanden das Ergebnis – also die Summe – nicht verändert (Kommutativgesetz). Bei Thematisierung der Subtraktion kommt es deswegen häufig vor, dass Kinder diese Regel, die sie bei der Addition bereits kennengelernt haben, unreflektiert auf die Subtraktion übertragen.
Melissa hat somit die Subtraktionsaufgabe „46-28“ nach ihrem Wissensstand gelöst.
Aufgabenauswahl – Fehler identifizieren
Sicherlich hätte Melissa ohne Probleme die Aufgabe 48-26 mit ihrer Strategie - zuerst die Zehner, dann die Einer voneinander abziehen - lösen können. Doch wäre dabei nicht ersichtlich geworden, dass Melissa das Kommutativgesetz der Addition auf die Subtraktion überträgt. Dazu war es notwendig einen kleineren Einer im Minuenden zu wählen und einen größeren Einer im Subtrahenden, wie die Aufgabe 46-28.
Im Unterricht sollten daher bewusst auch Aufgaben ausgewählt werden, die die Kinder herausfordern, bei denen die Kinder ihre individuellen Lösungswege gehen können und ihre individuelle Denkweisen offenlegen können, die sie zu diesem Zeitpunkt haben.
Diese Aufgaben dienen somit als Diagnoseinstrument um herauszufinden, ob die Kinder möglicherweise noch Schwierigkeiten in einem Bereich haben – wie im Fall von Melissa mit dem Entbündeln vom nächsten Zehner des Minuenden.
Die Lehrperson kann sich dabei folgende Fragen stellen: Wo ist das potenzielle Problem bei der Aufgabe? Wie hat das Kind die Aufgabe gelöst? Was war für das Kind noch schwierig?
Auch sogenannte „informative Aufgaben“ haben ein großes Potential um individuelle Vorgehensweisen zu ermöglichen und diagnostizieren zu können. Sie fördern dabei auch die prozessbezogenen Kompetenzen.
Wie informativen Aufgaben konkret im Unterricht eingesetzt werden können und was diese Art von Aufgaben ausmacht kann auf unserer Partnerseite PIKAS: Unterrichtsmodul: 'Leistung - Mathebriefkasten' und auf dieser Seite unter Gute Aufgaben genauer nachgelesen werden.
Produktiver Umgang – Fehler für reflexive Unterrichtsgespräche nutzen
Die Frage, die sich stellt: Wie gehe ich als Lehrkraft nun konkret mit den Fehlern um? Es ist wichtig, dass mit den Kindern über die identifizierten Fehler gesprochen wird und eine kompetenzorientierte Sichtweise erfolgt, d.h. geschaut wird, was das Kind bereits gut gelöst hat und warum es diese Aufgabe so gelöst hat. Erst wenn das Kind seinen Fehler einsieht und versteht, kann es offen sein für eine neue Vorgehensweise und diese nachvollziehen.
Es bietet sich oftmals an, den lokalisierten Fehler – im Fall von Melissa also das Vertauschen der Einer des Minuenden und Subtrahenden - als Ausgangspunkt für ein Unterrichtsgespräch zu nutzen: „Warum darf ich bei Minusaufgaben eigentlich die beiden Zahlen nicht vertauschen, so wie ich es beim Plusrechnen immer gemacht habe?“
Dadurch wird nicht nur das Einzelgespräch mit einem Kind über sein Fehler geführt, sondern ein Fehler kann ebenfalls in fiktiver Form im Klassenverband thematisiert und somit als Lerngelegenheit für alle genutzt werden. Achtung: Dabei sollte kein einzelnes Kind vor der ganzen Klasse vorgeführt werden!
Und wie kann das Kind den Fehler verstehen und seine Vorgehensweise ändern?
Es ist häufig gar nicht notwendig und auch nicht sinnvoll, die Kinder auf einen ganz anderen Weg zu bringen. Ohne Einsicht in ihren eigenen Fehler besteht die Gefahr, dass Kinder den neuen Weg ohne Verständnis wie ein Regelwerk verwenden. Vielmehr sollten die fehlerhaften Vorgehensweisen der Kinder gemeinsam betrachtet und – wo möglich - korrigiert werden um aus den Fehlern bedeutsame Erkenntnis für das weitere Lernen zu gewinnen.
Im Fall von Melissa: Hätte sie im Folgenden die 2 als „noch abziehend“ interpretiert und sie entsprechend von 20 subtrahiert, wäre ihre Rechnung auch korrekt gewesen. Doch ob sie dann überhaupt ihren Rechenweg verstanden hätte, bleibt dabei fraglich.
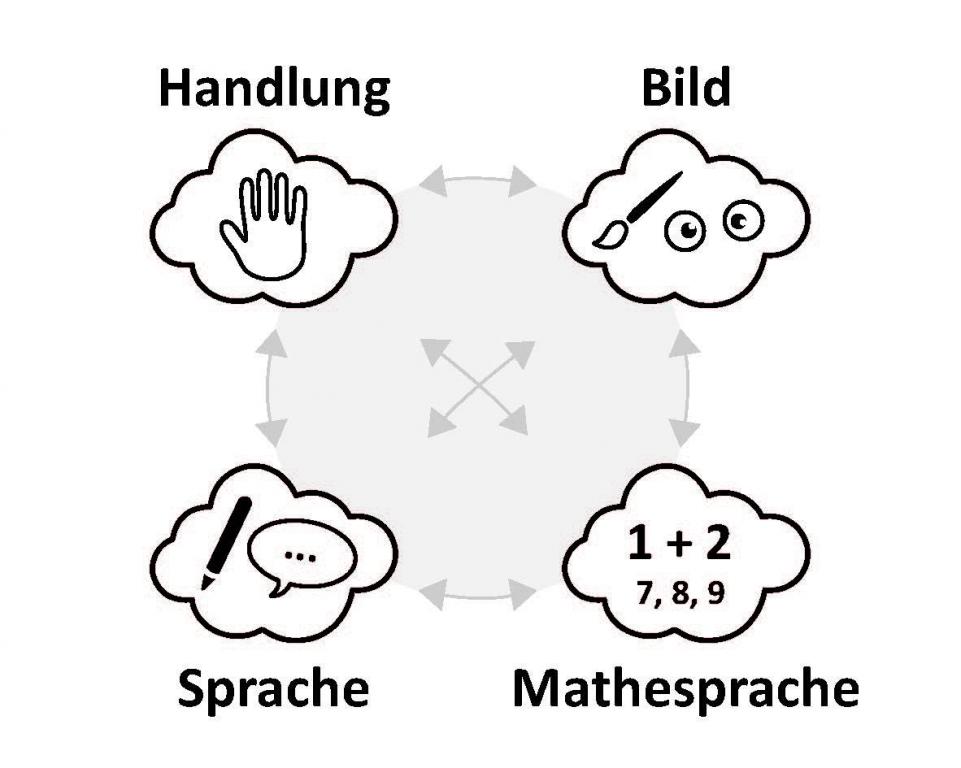
Zur Einsicht in Melissas Fehler – so wie auch in viele andere Fehler - ist es daher ratsam, von Melissa sogenannte Darstellungswechsel zu fordern und zu fördern. Dadurch kann Melissa verstehen lernen, was es bedeutet zu subtrahieren. Bei einemDarstellungswechsel (Pfeile in der Abb.) können die Kinder Wechsel zwischen den Darstellungsformen (Handlung, Bild, Sprache und Mathesprache) vollziehen.
Mit Melissa könnte die Aufgabe „46-28“ handelnd oder zeichnerisch im Bild (siehe Abbildung) nachvollzogen werden. Dabei sollte dieses Vorgehen unbedingt auch sprachlich begleitet werden: „Warum passt die Zeichnung zur Aufgabe? Wo siehst du 40-20? Wo siehst du 6-8?...“. Die Problematik des ‚Abziehens vom kleineren Einer‘ kann insofern gelöst werden, dass mit dem Kind vereinbart wird, es schreibt ein Minuszeichen vor das Zwischenergebnis und merkt sich dann, dass dafür der nächste Zehner „angebrochen“ werden muss.

Auf den Seiten Stellenwertverständnis, Operationsverständnis und Materialeinsatz können Sie zum Darstellungswechsel und den Darstellungsformen weitere Hinweise nachlesen.
Zusammenfassend lässt sich festhalten, dass im Mathematikunterricht die Grundhaltung vermittelt werden sollte, dass Fehler als Lerngelegenheiten für die ganze Klasse betrachtet werden, die gewinnbringend sind. Daher ist es wichtig immer wieder bewusst „kognitive Konflikte“ bei den Kindern herzustellen durch eine geeignete Aufgabenauswahl und – wenn es Sinn macht - die Fehler in Form fiktiver Schülerlösungen auch im Klassenverband zu thematisieren.
Weiterführende Anregungen zur Subtraktion finden Sie bei unserem Partnerprojekt:
KIRA: Halbschriftliche Subtraktion