Darstellen

Darstellen ist das Veranschaulichen und Repräsentieren mathematischer Sachverhalte. Darstellen im Zusammenhang mit den Bildungsstandards wird auch als jegliche Art der Veräußerungen des Denkens durch die Kinder verstanden (vgl. Krauthausen & Scherer 2007).
Welche Kompetenzen sollen Kinder bis zum Ende der Grundschulzeit in diesem Bereich erwerben? In den KMK-Bildungsstandards wird das wie folgt beschrieben:

• für das Bearbeiten mathematischer Probleme geeignete Darstellungen entwickeln, auswählen und nutzen
• eine Darstellung in eine andere übertragen,
• Darstellungen miteinander vergleichen.

(vgl. KMK 2004, S. 8)

Veranschaulichen und Repräsentieren mathematischer Sachverhalte – materialgebundene und bildliche Darstellungen

Mathematische Sachverhalte, Begriffe und Operationen können durch materialgestützte Handlungen, Bilder, mündliche und schriftsprachliche Darstellungen repräsentiert und veranschaulicht werden.
Insbesondere materialgebundene und bildliche Darstellungen unterstützen Kinder dabei, sich einen mathematischen Inhalt zu erschließen und sich selbst ein inneres Bild aufzubauen. Das ist grundlegend für ein verständnisbasiertes Lernen von Mathematik. Umgekehrt bedeutet das, wenn Kinder nicht ausreichend Gelegenheit erhalten in dieser Form zu arbeiten, können Schwierigkeiten im Lernen auftreten.

Beispielhaft wird an dieser Stelle einer Divisionsaufgabe auf verschiedenen Repräsentationsebenen dargestellt:
... handelnd materialgestützt (Verteilen oder Aufteilen)

... veranschaulicht in Punktbildern

... symbolisch (Ziffern im Positionssystem und Operationszeichen)

24 : 4

Das Wechseln zwischen den verschiedenen Repräsentationsebenen ist eine Herausforderung für die Kinder. Diesen Wechsel zu vollziehen, verlangt Übersetzungsleistungen, die für ein Verständnis der Division unerlässlich sind.
Die in diesem Beispiel genutzen Plättchen zeigen, dass Darstellungsmittel nicht nur in der Einführung von mathematischen Inhalten genutzt werden sollten. Sie dienen auf der einen Seite dem Verstehen des Sachverhalts, dem Entdecken von Mustern und Strukturen und dem Begründen. Auf der anderen Seite können mit ihnen Vorgehensweisen bzw. Ergebnisse dokumentiert und Austauschprozesse unterstützt werden.

Auf den Seiten unserer Partnerprojekte finden Sie weitergehende Informationen und Anregungen:

• PIKAS: Haus 3 - Guter Umgang mit Darstellungsmitteln
• KIRA: Bildliche Darstellung (hier wird gezeigt, worauf man beim Einsatz achten sollte und welche Schwierigkeiten dabei auftreten können.)

Lernwege dokumentieren

Im Lernprozess versuchen die Kinder oft, zunächst Aufgaben im Kopf zu lösen und beschreiben ihr Vorgehen mündlich unter Nutzung der Umgangssprache. Kinder sollen angeregt werden, ihre eigenen Wege, ihr Vorgehen und die Ergebnisse von Arbeitsprozessen zu dokumentieren. Das kann in unterschiedlicher Art und Weise erfolgen. Die Darstellungen der Kinder sind individuell und unterscheiden sich qualitativ.

Skizzen zum Veranschaulichen des Lösungsweges

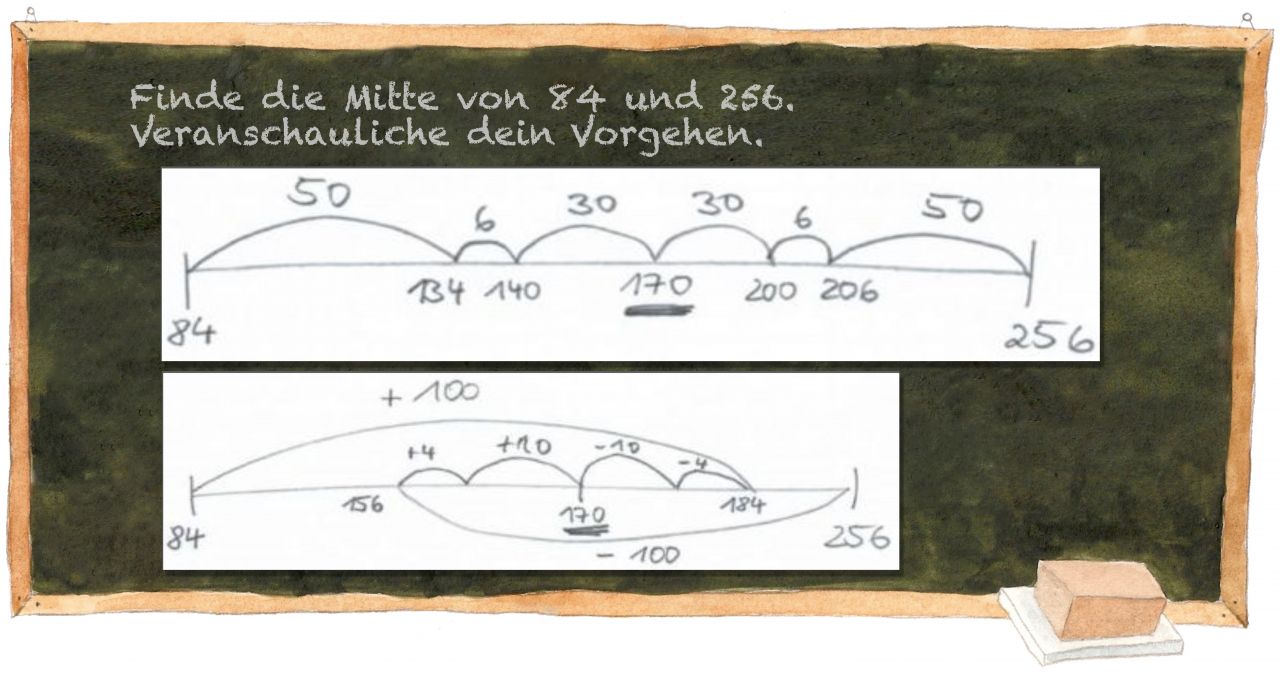
Die Kinder haben für die Darstellung ihrer Lösungswege einen Zahlenstrich ausgewählt. Diese Darstellung ist geeignet, weil man das Vorgehen nachvollziehen und vergleichen kann.

Überlegungen verschriftlichen

Auftrag:

Würfle 30-mal und führe eine Strichliste. Was fällt dir auf? Versuche deine Entdeckungen zu begründen.

Aufzeichnungen der Kinder bieten Lehrpersonen die Möglichkeit, Einblick in das Denken und Verständis der Kinder zu bekommen. In diesem Beispiel kann man erkennen, dass das Kind sein Versuchsergebnis auf der Grundlage der eigenen Spielerfahrungen beurteilt.

Bildliche Darstellung der Lösung

Auftrag:

Der Eisverkäufer bietet drei Sorten an: Schoko-, Vanille- und Himbeereis. Nina, Tina und Lina möchten sich ein Eis kaufen. Jedes Kind hat Geld für zwei Kugeln Eis. Finde verschiedene Möglichkeiten!

Dieses Kind stellt die Situation so dar, wie es vermutlich seiner Erfahrungswelt entspricht. Dazu gehört der Eismann mit Eiswagen und Sonnenschirm und natürlich das Kind selbst. In dieser Zeichnung finden wir auch alle Lösungen der Aufgaben. Bereits mit Erstklässlern kann am Beispiel einer derartigen Darstellung besprochen werden, was an einer zeichnerischen Darstellung das Wesentliche ist, damit man eine Lösung finden kann.

Eine Darstellung in eine andere übertragen

Dieses Kind hat nach Vorgaben ein Haus aus gelben und roten Steckwürfeln gebaut. Diese (räumliche) Darstellung wurde von ihm im Anschluss in eine bildliche übertragen.

Da der Körper – je nach Perspektive – verschieden aussieht, wurden zwei Ansichten gezeichnet.

Darstellungen miteinander vergleichen

Im folgenden Beispiel erscheint es sicher zunächst sinnvoll, jede Darstellung gesondert zu betrachten und zu klären, welche Informationen entnommen werden können. Im Anschluss kann es interessant sein, zu untersuchen, wie die Informationen der einzelnen Diagramme zusammenhängen. Im Weiteren kann besprochen werden, welches Diagramm für welche Fragestellung besonders geeignet ist.

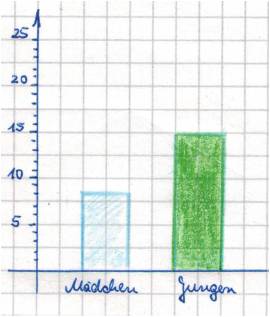
(vgl. auch Binner & Grassmann 2015)

Die hier beschriebenen Arbeitsweisen zeigen die enge Vernetzung der allgemeinen mathematischen Kompetenzen. Darstellunen sind Teil von Problemlöseprozessen und hilfreich beim Modellieren. Sie regen zum Kommunizieren an und provozieren das Argumentieren.

• Skizzen helfen, einen Sachverhalt zu verstehen und zu vereinfachen.
• Tabellen eine übersichtliche Form der Dokumentation von Ergebnissen experimentellen Arbeitens sein können.
• eine Dokumentation – zunächst egal in welcher Form – die Kommunikation mit den anderen Lernenden unterstützt.
• Lesbarkeit, Übersichtlichkeit und auch die adressatengerechte Darstellung von Überlegungen das Verstehen von Vorgehensweisen und Ergebnissen erleichtert.

• Weitere Anregungen

Weitere Aussführungen und Anregungen für den Unterricht finden Sie auf den Seiten unserer Partnerprojekte:
KIRA: Prozessbezogene Kompetenzen fördern - Beispielaufgaben
PIKAS: Haus 1 - Informationstexte: Prozess- und inhaltsbezogene Kompetenzen - Illustration durch zehn Unterrichtsbeispiele