Gemeinsames Lernen der Kinder lebt von vielfältigen Kommunikationsprozessen. Um Arbeitsprozesse in der Mathematik allein und in der Gruppe effizient gestalten zu können, sollen Kinder im Laufe der Grundschulzeit im Bereich Kommunizieren folgende Kompetenzen erwerben:
-
eigene Vorgehensweisen beschreiben, Lösungswege anderer verstehen und gemeinsam darüber reflektieren,
-
mathematische Fachbegriffe und Zeichen sachgerecht verwenden,
-
Aufgaben gemeinsam bearbeiten, dabei Verabredungen treffen und einhalten.
(vgl. KMK 2004, S. 8)
Kommunizieren ist mit allen anderen allgemeinen mathematischen Kompetenzen vernetzt, insbesondere mit dem Argumentieren. So werden Kinder bereits beim Austausch zu Lösungswegen Aussagen hinterfragen und auf Korrektheit prüfen (Argumentieren). Der Bezug zur Gestaltung eines sprachsensiblen Mathematikunterrichts wird u. a. auf den Seiten zur Sprachförderung hergestellt.
Die eigenen Vorgehensweisen beschreiben, Lösungswege anderer verstehen und gemeinsam darüber reflektieren
Um Fähigkeiten im Beschreiben zu entwickeln, sollten Aufgaben genutzt werden, die nicht nur formal zu lösen sind. So bietet beispielweise eine Einbindung in Aufgabenpakete Spielraum zum Erforschen und Entdecken. Aufträge wie Rechne aus. Was fällt dir auf ? fordern gezielt entsprechende Schülertätigkeiten heraus.
Bilder zum Vergrößern anklicken



In den Schülerdokumenten ist zu erkennen, dass Kinder oft farbliche Kennzeichnungen nutzen, um ihre Entdeckungen hervorzuheben. Um den Überblick nicht zu verlieren, wird auch schon einmal eine (Farb-)Legende angelegt (mittlere Abb.). Die Beschreibungen erfolgen dann mithilfe dieser Darstellungen mündlich. Zum Verschriftlichen ihrer Überlegungen müssen Kinder immer wieder angeregt, ermutigt und gefordert werden.
Kinder beschreiben ihr Vorgehen und ihre Entdeckungen und verstehen, wie andere die Aufgabe bearbeitet haben. Das Reflektieren der Arbeitsphase ermöglicht das Vergleichen von Lösungswegen und fördert damit einerseits die Erkenntnis, dass es zu einer Aufgabe unterschiedliche Lösungsansätze geben kann. Andererseits werden in der Diskussion tragfähige Strategien und (allgemeingültige) Zusammenhänge herausgefunden.
Aufgaben, die diese Kompetenzentwicklung ermöglichen, werden in der fachdidaktischen Literatur als "gute" Aufgaben bzw. substantielle Aufgabenformate bezeichnet. Die Erweiterung auf Lernumgebungen nimmt die Einbindung der Aufgabe in und die Gestaltung des Unterrichts mit in den Blick. Informieren Sie sich dazu auch auf der Seite Unterricht – Mehr als gute Aufgaben.
Weitere Anregungen finden Sie auch auf den Seiten der Partnerprojekte:
Mathematische Fachbegriffe und Zeichen sachgerecht verwenden
Bereits mit Schuleintritt sollen Kinder ermuntert und gefordert werden, ihre Überlegungen und Ideen mit anderen auszutauschen. Das ist zu Schulbeginn zunächst nur mündlich möglich und erfolgt im Rahmen der individuellen sprachlichen Fähigkeiten und Ausdrucksmöglichkeiten.
Bei den Äußerungen der Kinder sollte darauf geachtet werden, dass der mathematische Sachverhalt sachlich korrekt beschrieben wird. Fachbegriffe und Zeichen werden erst dann eingeführt, wenn es sinnvoll und zweckmäßig erscheint.
Inwieweit die Fachbegriffe in den aktiven Wortschatz der Kinder übergehen und sachgerecht gebraucht werden, hängt maßgeblich davon ab, inwieweit sie inhaltlich verstanden wurden und im Unterricht verwendet werden. Informieren Sie sich dazu auch auf der Seite Sprachförderung.
Aufgaben gemeinsam bearbeiten, dabei Verabredungen treffen und einhalten
So genannte Rechen- oder Mathe-Konferenzen sind ein geeignete Methode, um Kommunikationsprozesse im Unterricht zu initiieren und Kinder aktiv an Arbeitsprozessen teilhaben zu lassen. Als Rechen- oder Mathe-Konferenz bezeichnet man einen Zusammenschluss von Kindern in heterogenen Kleingruppen zur Präsentation und Reflexion von individuellen Lösungswegen im Mathematikunterricht (vgl. Sundermann & Selter 1995).
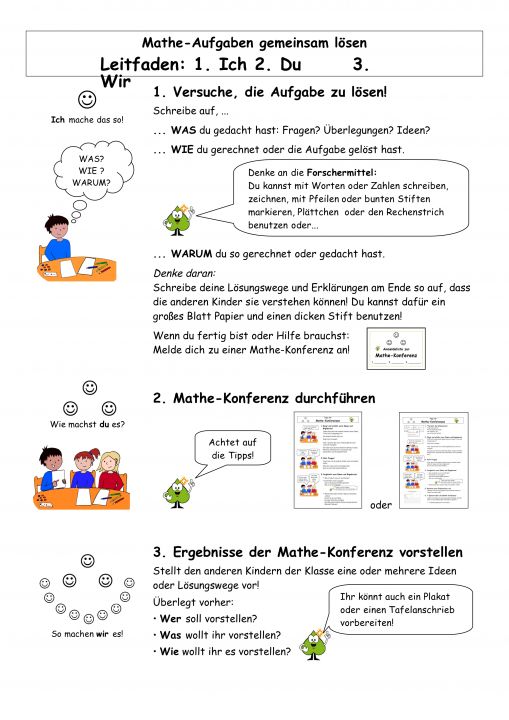
Der Ablauf wird durch das Ich-Du-Wir-Prinzip bestimmt.
Kinder haben zunächst die Möglichkeit, eigene Lösungswege zu suchen und zu dokumentieren (Ich-Phase). Im weiteren Arbeitsprozess kann es in den Austausch mit andern Kindern treten. Ziel dieser (Du-)Phase ist es, die sachbezogene Kommunikation zu fördern, indem die Kinder sich gegenseitig über ihre Lösungswege informieren und sie miteinander vergleichen. Gemeinsamkeiten und Unterschiede herauszustellen hilft, Irr- und Umwege zu erkennen, tragfähige Strategien zu benennen, Zusammenhänge herzustellen und Verallgemeinerungen zu begründen. Die Ergebnisse der Austauschprozesse werden im Klassenverband präsentiert und zur Diskussion gestellt (Wir-Phase).
Wie jede andere Methode muss zunächst auch eine Mathe-Konferenz eingeführt und ritualisiert werden. Dazu finden Sie Hinweise und Materialien auf unserer Partnerprojektseite PIKAS: Unterrichtsmodul: 'Sprachbildung- Mathekonferenzen' .
Je häufiger die Kinder die Möglichkeit erhalten in dieser Form zu arbeiten, desto mehr werden sie befähigt, Mathe-Konferenzen aktiv mitzugestalten. Auf diese Art und Weise werden neben der Entwicklung kommunikativer auch darstellende und argumentative Kompetenzen der Kinder gefordert und gefördert.