Hintergrund

Der Sinn des Spiralprinzips

Mit dem Schuleintritt sind die mathematischen Alltagserfahrungen und das Vorwissen der Kinder zu ergründen, systematisch zu erweitern und zu vertiefen. Diese langfristig angelegten Lernprozesse sind so zu gestalten, dass einerseits anschlussfähiges Lernen innerhalb der Grundschule gesichert ist. Darüber hinaus sollen auch "die Grundlage für das Mathematiklernen in den weiterführenden Schulen und für die lebenslange Auseinandersetzung mit mathematischen Anforderungen des täglichen Lebens geschaffen werden" (KMK 2005, S. 6).

Wie das konkret umgesetz werden kann, wird im Folgenden angesprochen:

• Was bedeutet das `Spiralprinzip´?
• Warum ist eine Unterrichtsplanung nach dem Spiralprinzip wichtig?
• Welche Konsequenzen und Herausforderungen gibt es bei der Unterrichtsplanung?

Was bedeutet das 'Spiralprinzip'?

Das 'Spiralprinzip', wie Bruner (1973) es nennt, bedeutet, dass

Inhalte in mehreren Durchgängen auf jeweils verschieden hohem Niveau bearbeitet werden [sollten], wobei jeweils Darstellungsmittel, Sprache und didaktische Modelle verwendet werden, die dem Entwicklungsstand der Schüler angemessen sind.

Das heißt Lernen erfolgt in einer Rück- und Vorschau. Bezogen auf das Eingangsbeispiel bedeutet Rückschau: die Rechenstrategien aus dem kleineren Zahlenraum werden erneut aufgegriffen und damit wiederholt. Lernen in der Vorschau bedeutet, dass man den Kindern z.B. über Themenleinen oder über den Einsatz von Kinderlehrplänen verdeutlicht, dass und wie mathematische Inhalte über die Schuljahre hinweg zusammenhängen. Beispiele dazu finden Sie auf der Seite unseres Partnerprojekts PIKAS: Unterrichtsmodul: 'Leistung - PIK-Plakat'. Es geht also nicht darum, etwas auswendig zu lernen und wieder zu vergessen, sondern den Kindern zu verdeutlichen, dass die mathematischen Lerninhalte zunehmend aufeinander aufbauen.

Das Spiralprinzip (vgl. Bruner,1973) bezeichnet die Idee, dass

• mathematische Inhalte und Prozesse (Kompetenzerwartungen im Lehrplan wie z.B. Zahlen und Operationen aber auch Problemlösen...)
• Aufgaben/-formate (zum Beispiel Zahlenmauern, Entdeckerpäckchen, Plusaufgaben mit Reihenfolgezahlen,...)
• und Materialien/Darstellungsmittel (zum Beispiel Punktefelder zur Zahlraumerweitung, als geometrisches Hilfsmittel, zur Veranschaulichung von Entdeckungen,...)

in den einzelnen Schuljahren wiederkehrend aufgegriffen, daran bewusst angeknüpft und das bereits bestehende Wissen vertieft werden (vgl. Schwätzer 2009, S. 554).

Im Sinne des Spiralprinzips zu unterrichten bedeutet, Vorwissen bewusst zu aktivieren und zu verknüpfen. Es wird bei einer erneuten Begegnung der jeweiligen Entwicklungsstufe angepasst (siehe nebenstehende Abbildung – in Anlehnung an Büchter (2014)). Dabei ist darauf zu achten, dass es in den späteren Schuljahren fortsetzbar und somit ein Ausbau auf höherem Niveau möglich ist (vgl. Wittmann 1981, S. 86).

Für die Unterrichtsplanung bedeutet das, dass folgende Aspekte berücksichtigt werden sollten:

• das "vorausgreifende Lernen", d.h. es wird nicht gewartet, bis das gesamte Wissensgebiet verstanden werden kann, sondern es wird in einfacher Form und Struktur bereits vermittelt, z.B. werden Brüche und Dezimalzahlen wie 1,25 Euro und 1/4 Milch, die den Kindern aus dem Alltag bekannt sind, bereits in der Grundschule angesprochen
• und die "Fortsetzbarkeit", d.h. das Wissensgebiet kann zukünftig inhaltlich im Umfang erweitert und vertieft werden. Wie bereits im Einstiegsbeispiel aufgeführt können Möglichkeiten und Grenzen der Übertragbarkeit von Rechenstrategien auf einen größeren Zahlenraum und anderen Zahlbereich (wie Brüche) erfahrbar gemacht werden.

Betrachtet man Material und Darstellungsmittel, so bieten sich zur Veranschaulichung von Rechenstrategien beispielsweise Punktefelder an, da diese strukturgleich fortgesetzt werden können, der Zahlenraum problemlos erweiterbar und somit ein Einsatz im Sinne des Spiralprinzips möglich ist (vgl. nebenstehende Abbildung).
Ein Unterricht im Sinne des Spiralprinzips greift idealerweise auf mehreren Ebenen: Die Kinder kennen einerseits das Material des Zwanzigerfeldes aus dem ersten Schuljahr. Sie wissen, dass und wie Zahlen mit Hilfe von Fünfern und Zehnern schnell gelegt und gelesen werden können. Dieses Wissen wird analog auf den Hunderterraum übertragen: Eigentlich ist es nichts Neues.

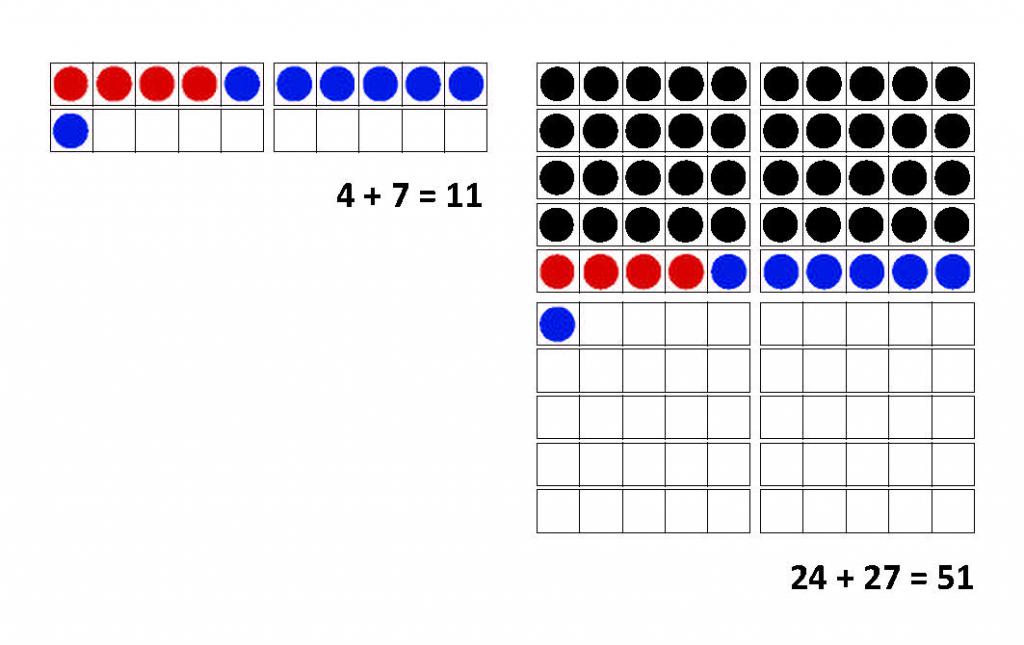
Auf der anderen Seite werden bewusst die einfachen Aufgaben aus dem Zwanzigerraum genutzt, um die vermeintlich schwierigen Aufgaben im Hunderterraum zu lösen: Wenn wir doch schon wissen, dass 4 plus 7 11 ergibt, dann kann uns das doch helfen, die Aufgabe 24 plus 27 zu berechnen. Die Frage, die sich stellt lautet: Wie können uns die einfachen Aufgaben helfen, schwierige Aufgaben zu lösen? Das Wissen über Rechenstrategien wird insofern ausgeweitet. Rechenstrategien werden NICHT neu gelernt, sondern mit bereits bestehenden verknüpft.

Warum ist eine Unterrichtsplanung nach dem Spiralprinzip wichtig?

Das Spiralprinzip stellt ein grundlegendes Prinzip der Unterrichtsplanung und -gestaltung in der Mathematikdidaktik dar. Es beeinflusst die Auswahl von mathematischen Inhalten, die Nutzung ausbaufähiger Aufgabenformaten und die Einbindung geeigneter Materialien. Aber warum ist das so wichtig?

Auf der Basis, eine Thematik auf unterschiedlichen Niveaustufen mit verschiedenen Schwerpunkten im Unterricht zu betrachten, wird für die Lernenden der Grundstein für ein effektives und verstehensorientiertes Lernen gelegt. Die Kinder können ihr Wissen zu einer Thematik dadurch besser vernetzen, abspeichern und in Verbindung bringen. Daher ist das Spiralprinzip eine wichtige Grundlage für den Aufbau und die Planung des Unterrichts (vgl. Büchter 2014, S. 3).

Wird der Mathematikunterricht im Sinne des Spiralprinzips gestaltet, kann er auch der Heterogenität der Kinder leichter gerecht werden. Auf der einen Seite kann jedem Kind ein Zugang zum mathematischen Inhalt gesichert werden, indem die Anforderungen dem individuellen Lernprozess der Kinder angepasst und entsprechend reduziert werden, ohne dabei den mathematischen Kern zu verfälschen. Auf der anderen Seite ermöglichen ausbaufähige Aufgabenformate eine Erweiterung des Anforderungsniveaus.
Natürlich bringt dies Konsequenzen sowie Herausforderungen für die Lehrperson hinsichtlich der Unterrichtsplanung mit, auf die im Folgenden eingegangen wird.

Welche Konsequenzen und Herausforderungen gibt es bei der Unterrichtsplanung?

Langfristiges Denken als Konsequenz

Mit der Vorgabe von ausdifferenzierten Kompetenzerwartungen am Ende der zweiten und der vierten Klasse geben Lehrpläne und auch die Bildungsstandards eine Orientierung für eine langfristige Unterrichtsplanung im Sinne des Spiralprinzips.

Um ein anschlussfähiges Lernen über alle Schulstufen hinweg zu sichern, bauen die Bildungsstandards, aber auch die Kompetenzerwartungen in den landesspezifischen Lehrplänen aufeinander auf.
Für die Sicherung der Kompetenzentwicklung ist eine schulinterne Planung, die sich am Spiralprinzip orientiert, an der Schule notwendig. Sie ist in der mittel- und kurzfristige Unterrichtsplanung, die der Lehrperson obliegt, für die jeweilige Klasse zu konkretisieren.
Bei der mittelfristigen Unterrichtsplanung werden Halbjahres- und Reihenplanungen im Kollegium entwickelt und bei der kurzfristigen Unterrichtsplanung wird die nächste Unterrichtsstunde vorbereitet. Doch ist auch bei dieser Planung immer ein ‚Mitdenken in Form des Spiralprinzips’ aus den bereits genannten Gründen wichtig. Zugleich ergeben sich dadurch natürlich auch Herausforderungen, auf die im Folgenden nur kurz eingegangen wird.

Herausforderungen bei der Unterrichtsplanung

Zu den Herausforderungen, die bei der Unterrichtsplanung gemäß dem Spiralprinzip geleistet werden müssen, zählen:

Vorwissen der Lerngruppe berücksichtigen

Es ist wichtig das Vorwissen der Kinder zu einem Inhalt vorab zu ermitteln um sicherzustellen, dass alle Kinder über die notwendigen Voraussetzungen für die nächste Unterrichtsreihe verfügen oder die notwendigen Anpassungen des Inhalts vornehmen zu können. Dazu eignen sich Standortbestimmungen genauso gut wie Eigenproduktionen von Kindern.
Weitere Anregungen zur Erhebung von Lernvoraussetzungen erhalten sie in unserem Selbstlernmodul Standortbestimmungen.

Über die Schulstufen hinaus denken

Um das Spiralprinzip erfolgreich bei der Unterrichtsplanung zu berücksichtigen, ist eine sorgfältige Analyse der fachlichen Gegenstände unumgänglich.Wie stehen sie in Verbindung zu vorangehenden und nachfolgenden Themen?
Oft sind Themen über mehrere Schulstufen hinweg „verteilt“. Daher ist es für die Lehrkraft jeder Stufe wichtig zu wissen, wie das Thema und die damit verbundenen grundlegenden Begriffe thematisiert wird bzw. wurde. Erst dann kann ein anschlussfähiges Lernen ermöglicht werden. Daher lohnt sich oftmals ein Blick in den Lehrplan der anderen Schulstufen. Auch ausgewählte Schulbücher anderer Schulstufen können hilfreich sein. Für die Kinder kann es hilfreich sein, mit einem Kinderlehrplan zu arbeiten. Einen solchen finden Sie auf unserer Partnerseite PIKAS: Unterrichtsmodul: 'Leistung - PIK-Plakat'.

Themen über die Schuljahre verteilen

Im Mathematikunterricht der Grundschule bieten sich insbesondere substanzielle Aufgaben für eine spiralige Wiederkehr innerhalb der Schuljahre und über die Schuljahre hinweg an, wie beispielsweise das Aufgabenformat Zahlenmauern. Gute Aufgaben zu Zahlen- und Formenmuster, die im Unterricht in der Sekundarstufe unter steigendem Niveau und vertiefenden Problemstellungen erneut bearbeitet werden können, sind ebenfalls gut geeignet.
Wie der Unterricht nach dem Spiralprinzip aufgebaut sein kann und was dabei berücksichtigt werden sollte, wird im Unterrichtsteil anhand des Aufgabenformats "Plusaufgaben mit Reihenfolgezahlen" exemplarisch verdeutlicht.