Die schriftliche Subtraktion im Überblick
Im Folgenden möchten wir am Beispiel der schriftlichen Subtraktion (Entbündelungsverfahren) erläutern, wie eine verständige Einführung der schrifltlichen Rechenverfahren gestaltet werden kann. Diese Unterrichtsreihe finden Sie auch mit weiteren Materialien und Hinweisen auf den Seiten unseres Partnerprojektes PIK AS (o. J.) im Modul 5.2:
PIKAS: Fortbildungsmodul: Lernen auf eigenen Wegen – Vom Halbschriftlichen zum Schriftlichen.
Ziel der Unterrichtsreihe ist es, dass die Kinder die schriftliche Subtraktion verständig erwerben sollen, indem die halbschriftliche Strategie "Wechseln" ("Eintauschen") und das schriftliche Verfahren "Entbündeln" anhand gleicher Aufgaben gegenüber gestellt werden: Was ist gleich? Was ist verschieden? Voraussetzung dafür ist, dass die Kinder die halbschriftliche Strategie "Wechseln" ("Eintauschen") kennen.
Vom halbschriftlichen zum schriftlichen Subtrahieren
Folgende Punkte werden angesprochen:
Einstieg in die Unterrichtsreihe
-
Zu Beginn sollten die halbschriftlichen Rechenstrategien wiederholend thematisiert werden. Insbesondere die Strategie "Stellenweise subtrahieren mit Wechseln" (Wechseltrick) sollte im Zusammenhang mit dem Entbündelungsverfahren besprochen werden. Nutzen Sie das Dienes-Material, um mit den Kindern auf der Handlungsebene zu arbeiten.

-
Die obige Abbildung zeigt, wie man die Aufgabe 526 - 283 Schritt für Schritt handelnd mit der Strategie "Stellenweise mit Wechseln" löst. Die Kinder sollten anschließend auch auf der bildlichen Ebene diese Aufgabe lösen.
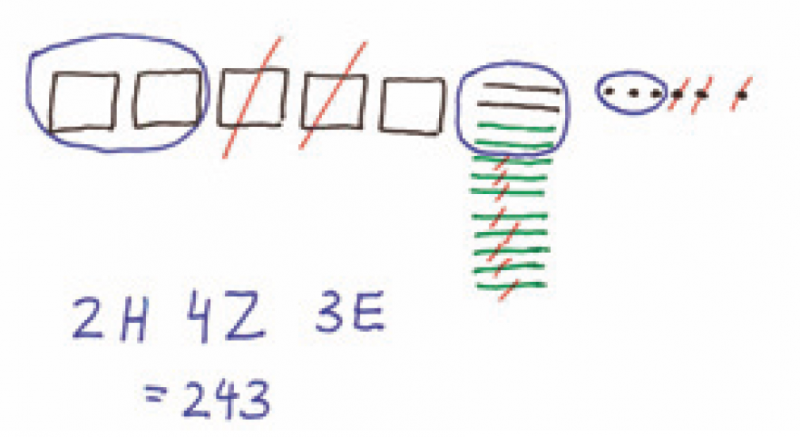
-
Ganz wichtig, sowohl auf der handelnden als auch auf der bildlichen Ebene, ist, dass Sie die Kinder die Handlungen sprachlich begleiten lassen: "6 Einer minus 3 Einer gleich 3 Einer. 2 Zehner minus 8 Zehner geht nicht. Ich wechsel eine Hunderter-Platte gegen 10 Zehner-Stangen. Es bleiben noch 4 Hunderter-Platten. 12 Zehner minus 8 Zehner gleich 4 Zehner. 4 Hunderter minus 2 Hunderter gleich 2 Hunderter. Das Ergebnis ist 243."
-
Bearbeiten Sie weitere Aufgaben auf diese Weise. Fordern Sie die Kinder auch immer wieder auf, die Materialhandlungen in Gedanken durchzuführen. Sie können die Kinder auch die Handlungen erklären lassen, während Sie hinter einem Sichtschutz die Handlungen entsprechend der Erklärungen mit Material ausführen. Am Ende kann der Sichtschutz entfernt und das Ergebnis verglichen werden. Auf diese Weise helfen Sie den Kindern, sich vom Material zu lösen.
Erarbeitung
-
Nun sollte die schriftliche Subtraktion eingeführt werden. Thematisieren Sie die Entbündelungstechnik im Plenum an der Tafel. Evtl. können die einzelnen Schritte parallel dazu mit Dienes-Material nachgelegt werden, um das Vorgehen noch anschaulicher zu machen.

-
Im nächsten Schritt sollten die halbschriftlichen Verfahren zu den schriftlichen Rechenverfahren in Beziehung gesetzt werden, damit die Kinder die Gemeinsamkeiten der beiden Rechenwege entdecken. Dies ist wichtig, damit die Kinder die Strategien und dessen Ausführung verstehen und nicht nur auswendig lernen.

Reflexion
-
Verwenden Sie ausreichend Zeit darauf, die Gemeinsamkeiten und Unterschiede dieser beiden Rechenverfahren mit den Kindern zu thematisieren. Lia hat beispielsweise sehr schön erkannt, dass es sich bei den schriftlichen Rechenverfahren lediglich um eine andere Form der Notation handelt und ansonsten die Ähnlichkeiten zum halbschriftlichen Rechnen sehr groß sind.

Ausblick
Wie kann man nun die schriftlichen Rechenverfahren
produktiv üben? Hier bietet sich das Format der ANNA-Zahlen an. ANNA-Zahlen sind vierstellige natürliche Zahlen, die wie Palindrome aufgebaut sind. Sie erfüllen folgende Bedingungen:
-
Alle Ziffern von 0-9 werden verwendet.
-
Die Tausender‐ und die Einerstelle sowie die Hunderter und die Zehnerstelle sind gleich.
-
Die ersten beiden Ziffern sind verschieden.
Beispiele: 3553, 6336, 8778 sind ANNA‐Zahlen. 9999 ist keine ANNA‐Zahl. Nachdem das Prinzip bekannt ist, bilden Kinder selbst ANNA-Zahlen und schreiben sie in großer Schrift auf vorbereitete Zettel. Die Systematik der ANNA-Zahlen regt Kinder dann zum Ordnen und Systematisieren an, z. B. an der Tafel.

Das entstehende Muster wird von den Kindern beschrieben und sie sollten argumentativ begründen, dass es genau 90 ANNA-Zahlen gibt. Tim sagt: "Da sind zwei Treppenmuster. Dazwischen sind Lücken. Das sind Zahlen mit immer vier gleichen Ziffern." Fordern Sie nun die Kinder auf, immer eine kleine ANNA-Zahl von einer größeren ANNA-Zahl zu subtrahieren. Was können die Kinder feststellen?
Es gibt insgesamt acht verschiedene Ergebnisse. Alle Ergebnisse sind Vielfache von 891. Aus der Differenz zwischen den Stellenwerten (Einer ‐ Einer usw.) lässt sich die Ergebniszahl vorhersagen und auch die Anzahl der Aufgaben zu jeder Ergebniszahl bestimmen. Weitere Ideen rund um das Thema ANNA-Zahlen finden Sie unter dem Menüpunkt
Material.
Wie kann es nun weitergehen?
Damit sich nun die schriftlichen Rechenverfahren nicht verselbstständigen und daraus doch noch ein Rechnen "ohne Nachdenken zu müssen" wird, sollten die Kinder auch nach der Einführung der schriftlichen Rechenverfahren dazu angehalten werden, im Kopf oder ggf. halbschriftlich zu rechnen, wenn eine Aufgabe besonders einfach ist. Weisen Sie die Kinder bei Hausaufgaben oder Klassenarbeiten explizit darauf hin: "Da sind Aufgaben zwischen, die könnt ihr im Kopf rechnen, wenn ihr den Zahlenblick habt!"
Einblicke in eine Unterrichtssequenz
Das ca. 15-minütige Video illustriert eine Einheit zu der Unterrichtsreihe "Vom halbschriftlichen zum schriftlichen Addieren und Subtrahieren - und zurück!", die nach den oben beschriebenen Prinzipien gestaltet ist.
Das Video hat dabei nicht den Anspruch "optimalen" Unterricht abzubilden, sondern versteht sich als Illustration eines möglichen Vorgehens und als Instrument der Ideenstiftung zur Planung des eigenen Unterrichtes und Reflexion über alternative Vorgehensweisen.
Auf der nächsten Seite finden Sie konkrete Materialien für Ihren Unterricht.