Üben mit "Entdecker-Päckchen"
In Übungsprozessen soll das beziehungsreiche Denken der Kinder durch die Einsicht in Zahlbeziehungen und Strukturen, sowohl anschaulich als auch formal, gefördert werden.
Viele Ihnen sicher bekannte Aufgabenformate (z. B. Rechendreiecke, Zahlenmauern etc.) eigenen sich für einen solchen aktiven Übungsprozess.
Jedoch fördern diese Aufgabenformate die genannten Einsichten nicht automatisch. Geeignete Aufgabenstellungen, die Auswahl des Zahlenmaterials und aktive Gesprächsanlässe sind dafür zentral (vgl. PIK AS 2009).
Aus diesem Grund soll im Folgenden am Aufgabenformat "Entdecker-Päckchen" vorgestellt werden, wie es im Sinne eines produktiven Übungsprozesses im Unterricht eingesetzt werden kann.
Auf dieser Seite werden dafür folgende grundlegende Informationen gegeben:
Das Aufgabenformat "Entdecker-Päckchen
Der folgende Filmausschnitt stellt das Aufgabenformat kurz vor und erläutert beispielhaft, was es zu einem "guten Aufgabenformat" im Kontext des "Übens" macht.
PIK AS o. J.
Der Einsatz von Entdecker-Päckchen bietet viele Möglichkeiten, Zahlbeziehungen zu entdecken und über diese ins Gespräch zu kommen. Zu Beginn soll das folgende Video einen ersten Einblick geben, wie Kinder mit "Entdecker-Päckchen" rechnen.
Das Video zeigt dabei Carla (2. Klasse), die ein Entdecker-Päckchen berechnet und dabei ihre Vorgehensweise und ihre Entdeckungen beschreibt.
KIRA 2011
Umsetzungsmöglichkeiten im Unterricht
Carlas Vorgehen und ihre Kompetenzen, Entdeckungen zu machen und Begründungen aufzustellen, bilden sich aber nicht bei allen Kindern wie selbstverständlich aus.
Das Erkennen und Nutzen von Zahlbeziehungen und Gesetzmäßigkeiten muss durch Lerngelegenheiten initiiert und gefördert werden, indem Kinder kontinuierlich in beziehungsreichen Zusammenhängen üben.
Das gelingt nicht allen Kindern gleich schnell und gleich erfolgreich, sodass es wichtig ist, die Kinder aufmerksam zu machen auf Zahlbeziehungen, Gesetzmäßigkeiten und Strukturen. Diese sollen aktiv entdeckt und dann im Unterricht zum konkreten Gesprächs- und Handlungsgegenstand werden.
Eigenaktivität
Sammeln Sie zunächst selbst Erfahrungen mit dem Format. Machen Sie aus den ungeordneten Aufgaben ein Entdecker-Päckchen (eine Aufgabe stört jedoch das Muster).
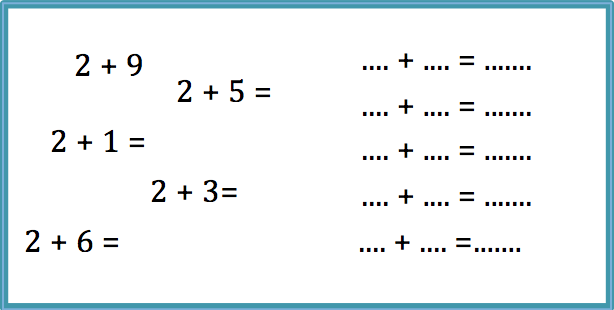
Vollziehen Sie nach, welche Schritte Sie zur Lösung der Aufgabe gegangen sind. Überlegen Sie dabei, welche Potentiale diese Aufgabe in Bezug auf das "beziehungsreiche Üben" hat.
Mögliche Aufgaben
Das Aufgabenformat der Entdecker-Päckchen ermöglicht es, unterschiedliche Schwerpunkte bezüglich der Förderung inhalts- und prozessbezogener Kompetenzen zu setzen.
Im Folgenden werden dazu beispielhaft mögliche Arbeitsaufträge für das 2./3. Schuljahr aufgezeigt und die Schwerpunktsetzung des verfolgten Zieles im Bezug auf das Üben konkretisiert.
Aber auch mögliche Schwierigkeiten bzw. zentrale Stellen ("Knackpunkte") im Lernprozess sollen aufgezeigt werden, um diesen vorbeugend begegnen zu können (vgl. KIRA o. J.).
Die Reihenfolge ist dabei nicht als starre Vorgabe anzusehen. Jedoch ist es sinnvoll, gewisse Variationen zu Beginn und andere erst zu einem späteren Zeitpunkt einzusetzen, da unterschiedliche Einsichten für weitere Bearbeitungen vorausgesetzt werden.
1. Entdeckungen ermöglichen
Arbeitsauftrag:
Zu Beginn sollten die Kinder eine Reihe von Entdecker-Päckchen ausrechnen und daraufhin angeregt werden, die Päckchen genauer zu untersuchen. Indem sie Strukturzusammenhänge erkennen und diese beschreiben, soll geklärt werden, warum diese Päckchen "Entdecker-Päckchen" heißen könnten.

Ziele
Ziele sind das Kennenlernen des Formats sowie das Aufmerksam-Machen auf mögliche Strukturzusammenhänge/Beziehungen zwischen den Aufgaben/Ergebnissen. Hier sollte auch ein Fokus darauf gelegt werden, die Kinder dazu erstmals anzuregen, zu überlegen, wie man die Entdeckungen darstellen könnte.
Mögliche Knackpunkte
Es wird vermutlich einige Kinder geben, die die existierenden Zusammenhänge bereits sehen oder gar nutzen und andere, die die einzelnen Aufgaben getrennt voneinander berechnen. Die Entdeckungen sollte zu einem zentralen Gegenstand des gemeinsamen Nachdenkens und Sprechens werden, um die grundlegenden Charakteristika und somit das Aufbauprinzip herauszuarbeiten und damit auch den Namen ,,Entdecker-Päckchen'' zu begründen. Hier können die Darstellungsmittel als eine zentrale Hilfe zur Verdeutlichung dienen.
2. Muster fortsetzen
Arbeitsauftrag:
Die Kinder sollen den vorgegebenen Anfang einer Aufgabenserie ausrechnen und diese nach dem entdeckten Zusammenhang fortsetzen. Dafür muss zuvor erarbeitet werden, dass ein Entdecker-Päckchen unendlich weitergeführt werden kann, wenn man den Aufbau beachtet.

Ziele
Die Kinder sollen das hineingelegte oder ein anderes von ihnen zu rechtfertigendes Konstruktionsprinzip erkennen und somit Beziehungen zwischen den Aufgaben herstellen. Diese sollen sie dann aktiv nutzen, sodass die Einsicht in Zahlbeziehungen und Gesetzmäßigkeiten geschult und übertragen wird.
Mögliche Knackpunkte
Es sollte nicht zu früh auf zu "schwere" Aufgabenserien zurückgriffen werden, sondern zunächst auch vergleichsweise simpel erscheinende Aufgabenserien eingesetzt werden (etwa solche mit einem konstanten Faktor), um diese Prozesse behutsam zu initiieren. Zunächst geht es darum, dass Beziehungen nicht nur entdeckt, sondern auch übertragen bzw. fortgeführt werden.
3. Störungen im Muster erkennen
Arbeitsauftrag:
Den Kindern wird eine Aufgabenserie vorge- geben, in der eine Aufgabe das Muster stört. Die Kinder sollen entscheiden, ob es sich um ein Entdecker-Päckchen handelt oder nicht und die "störende" Aufgabe identifizieren. Anschließend sollten sie aufgefordert werden, diese begründet durch die "Richtige" zu ersetzen.

Ziele
Die Kinder sollen über die Zusammenhänge zwischen den einzelnen Aufgaben und ihren Ergebnissen eben diese in Beziehung setzen und schulen dabei intensiviert die Einsichten in Zahlbeziehungen und Gesetzmäßigkeiten sowie den Zahlenblick/Aufgabenblick. Das Erkennen der "Störung" dient dabei der Überprüfung des erkannten Musters.
Mögliche Knackpunkte
Entdecker-Päckchen bergen die Gefahr, dass Kinder - sobald sie die Struktur einer Aufgabenserie erfasst haben - nicht mehr rechnen, sondern nur noch dem Muster folgen. Werden ausschließlich die vertikalen Muster der Entdeckerpäckchen fortgesetzt, ohne dass die horizontale Ebene betrachtet wird und keine Begründungen für die Veränderung angestrebt, schöpft das Aufgabenformat sein vollständiges Potenzial nicht aus. Mit der folgenden Aufgabenvariante kann man dem entgegenwirken, da die Kinder hier "gezwungen sind" zu rechnen. Greifen Sie auch hier zunächst auf "ersichtliche, einfache" Störungen zurück.
4. Aufgaben zu Entdecker-Päckchen ordnen
Arbeitsauftrag:
Die Kindern sollen eine durcheinander geratenen Aufgabenserie zu einem Entdecker-Päckchen ordnen. Eine Variation wäre es, auch hier eine Aufgabe einzubauen, die nicht in das Muster passt, und diese als Störung zu identifizieren.

Ziele
Bei diesen Variationen wird neben der Einsicht in die operative Struktur der Entdecker-Päckchen speziell auch der Zahlenblick geschult. Auch ohne zu rechnen sollen hier allein durch die Betrachtung der Zahlwerte die Aufgaben in Beziehung gesetzt werden.
Mögliche Knackpunkte
Kinder sind kreativ im Ordnen vorgegebener Aufgaben. Wichtig ist zunächst nicht, dass die Kinder die Antwort geben, die Sie aufgrund der Aufgabenzusammenstellung erwarten, sondern dass ihre Entscheidung aus ihrer Perspektive Sinn macht und sie diese begründen. Im Verlauf sollte dann verglichen und geklärt werden, welche "Ordnung" warum als sinnvoll erachtet werden kann und ob die Aufgaben und Ergebnisse wirklich in einer sinnvollen Beziehung zueinander stehen.
5. Beschreiben und Begründen des Musters
Arbeitsauftrag:
Die Kinder sollen dabei ihre gemachten Entdeckungen mündlich und/oder schriftlich beschreiben und begründen und auch auf Darstellungsmittel zurückgreifen. Dies stellt keine "gesonderte" Aufgabenvariation dar, sondern kann und sollte in jeder der Variationen angeleitet werden.

Ziele
Ziel ist das Erkennen, Beschreiben und Begründen der zugrunde liegenden Struktur (Fortsetzbarkeit des Musters) unter Berücksichtigung von Darstellungsmitteln als Instrument (Markieren, um zu entdecken) und Dokument (Markieren, um Anderen erklären zu können) des Lösungsprozesses. Der Schwerpunkt liegt in der Förderung der prozessbezogenen Kompetenzen (Problemlösen/Argumentieren), wobei aber stets die Addition mitgeübt wird.
Mögliche Knackpunkte
Inwieweit Kinder Darstellungsmittel zur Erläuterung und Begründung heranziehen, ist abhängig davon, ob sie diese als Hilfsmittel/Darstellungen kennengelernt haben und ob diese für sie zur Erhellung des Sachverhalt etwas beitragen. Dies muss gemeinsam thematisiert und gemeinsam eingeübt werden.
Die Ausführungen der Kinder werden sich in sprachlicher und mathematischer "Qualität" unterscheiden. Durch gewisse Hilfestellungen (z. B. Wortspeicher) sollte ein gemeinsamer Wortschatz aufgebaut werden. Diesen sollten Sie gemeinsam erarbeiten und selbst als Sprachvorbild dienen, indem sie diesen immer wieder nutzen und auch von den Kindern einfordern.
6. Entdeckerpäckchen erfinden
Arbeitsauftrag:
Die Kinder sollen bei dieser Version selbst Entdecker-Päckchen erfinden. Diese können durch Vorgabe gewisser Kriterien angeleitet werden.
-
Erfinde ein leichtes Entdecker-Päckchen!
-
Erfinde ein schweres Entdecker-Päckchen!
-
Erfinde ein Entdecker-Päckchen mit 4 + 8 als 4. Aufgabe und 5 + 10 als 6. Aufgabe!

Ziele
Durch die (adressatenbezogene) Produktion von (leichten und schwierigen) Entdecker-Päckchen werden die gewonnenen fachlichen und sprachlichen Erkenntnisse angewendet, vertieft und ggf. transferiert. Ferner wird die Methodenkompetenz der Kinder z. B. durch das Erproben dieser Aufgaben durch andere Kinder, Rückmelderunden und ggf. eine erfolgende Überarbeitung gefördert.
Mögliche Knackpunkte
Wahrscheinlich werden die Kinder nicht durchgängig ein Aufbauprinzip verwenden (Variation: Subtraktionsaufgaben; mehr als zwei Summanden etc.). Erkennen Sie die Erfindungen der Kinder an. Zeigen Sie, dass sie deren "Regeln" verstehen wollen und halten Sie die Kinder dazu an, zu begründen, warum es sich um ein Entdecker-Päckchen handelt und welche Struktur dahinter liegt.
Und: Nur weil ein Kind z. B. ein einfaches Muster wählt, heißt es nicht, dass es nicht in der Lage ist, ein schwierigeres Muster zu erfinden. Es sollte thematisiert werden, was ein Entdecker-Päckchen "leicht" und "schwer" macht (z. B. nicht nur die gewählten Zahlenwerte, sondern auch die Variation des Musters als Kriterium einzuführen).
Differenzierungsmöglichkeiten
Eigenaktivität
Schauen Sie sich an, wie Önder das Entdecker-Päckchen löst. Was fällt Ihnen auf?
KIRA o. J.
Das substantielle Übungsformat eignet sich im Besonderen auch für heterogene Lerngemeinschaften. Deutlich wird in den Ausführungen zu den Arbeitsaufträgen, dass sich Differenzierungsmöglichkeiten unter anderem von innen heraus ergeben, da alle Kinder an dem selben Lerngestand auf ihrem Niveau arbeiten können.
Sprachliche Ausdrucksweisen und die Art und Tiefe der Begründungen können sich stark unterscheiden. Jedes Kind kann dabei aber zunächst seinen eigenen Zugang finden.
Darstellungsmittel wie Markierungen helfen, Entdeckungen zunächst für sich und andere darzustellen. Plättchen ermöglichen es, die Auffälligkeiten zu begründen. In diesem Prozess kann jedes Kind Fortschritte erzielen und auf ein individuell gewähltes Mittel zurückgreifen.
Der Einsatz eines Wortspeichers ermöglicht dabei jedem Kind, inviduelle Fortschritte auch bezüglich der sprachlichen Kompetenzen zu machen.
Durch die Bereitstellung von "Tippkarten", in denen durch Markierungen oder "Tipps" auf die Strukturzusammenhänge hingewiesen werden, können auch Kinder, die zunächst Schwierigkeiten haben, diese Entdeckungen selbst zu machen, versuchen die Aufgaben in Beziehungen zu setzen und Strukturzusammenhänge dann gezielt zu untersuchen.
Durch die Wahl des Zahlenraumes und der Zahlwerte, so wie die "Art" der operativen Veränderung können die Entdecker-Päckchen auch gezielt differenzierte Anforderungsbereiche ansprechen, sodass Sie als Lehrkraft auch hier die Möglichkeit haben, jedem Kind gerecht zu werden.
Im Sinne des Spiralprinzips kann das Format dabei auch in und über unterschiedliche Klassenstufen hinweg eingesetzt werden.
Übungsaufgaben im eigenen Lehrwerk
Beziehungsreiche Übungsphasen sollten jedoch zu jeder Zeit in die verschiedenen Lernprozesse integriert werden. Es geht darum, kontinuierlich in Sinnzusammenhängen beziehungsreich zu üben, um Kenntnisse und Fertigkeiten zu festigen.
Substantielle Übungsformate wie Entdecker-Päckchen sollen nicht gesondert eingesetzt werden, um damit (für den eigenen Unterricht) das beziehungsreiche Üben "abzuhandeln".
Das eigene Lehrwerk kann bei einem reflektierten Einsatz reichlich Möglichkeiten bieten, denn auch viele Aufgaben in Ihrem eigenen Lehrwerk eignen sich durch kleine Veränderungen oder zusätzliche Arbeitsaufträge zum produktiven Üben.
Eigenaktivität
Schauen Sie sich folgenden Aufgabe aus einem Schulbuch an. Überlegen Sie, wie Sie im Sinne des produktiven Übens die Aufgabe zu einer produktiven Übungsaufgabe machen könnten.

So können in vielen Aufgaben durch kleine Veränderungen oder zusätzliche Arbeitsaufträge Strukturen und Beziehungen entdeckt werden. Diese müssen dann aber, wie oben erwähnt, zum zentralen Gegenstand des gemeinsamen Nachdenkens und Reflektierens werden.