Einstieg
Zahlenketten
In den Schulbüchern werden für Zahlenketten oft unterschiedliche Synonyme verwendet, wie beispielsweise Zahlenketten, Rechentürme oder Rechenzüge. Mal stehen aufrecht vier, fünf oder noch mehr Steinchen übereinander, mal liegen ähnlich viele Felder hintereinander.
Doch hinter all diesen Variationen verbirgt sich immer dasselbe Bildungsprinzip: Es werden zwei sogenannte Startzahlen beliebig gewählt und in den beiden linken (oder unteren) Feldern notiert. Das dritte Feld wird aus der Summe der beiden Startzahlen gebildet. In das vierte Feld wird wiederum die Summe aus dem zweiten und dritten Feld notiert. Jedes weitere Feld ist immer die Summe der beiden vorherigen Felder. Nach diesem Muster können Zahlenketten beliebig lang fortgesetzt werden.
Für die Startzahlen sind zahlreiche Möglichkeiten denkbar: Eine Startzahl kann Null betragen. Es könnten auch beide Startzahlen identisch sein. Zudem ist es auch möglich, dass die erste Startzahl größer ist als die zweite.
Schauen Sie sich nun die folgende Schülerlösung einer 2. Klasse an.
Um im Unterricht angemessen und sicher mit dem Aufgabenformat Zahlenketten umgehen zu können, widmen sich die folgenden Seiten diesen Fragen:
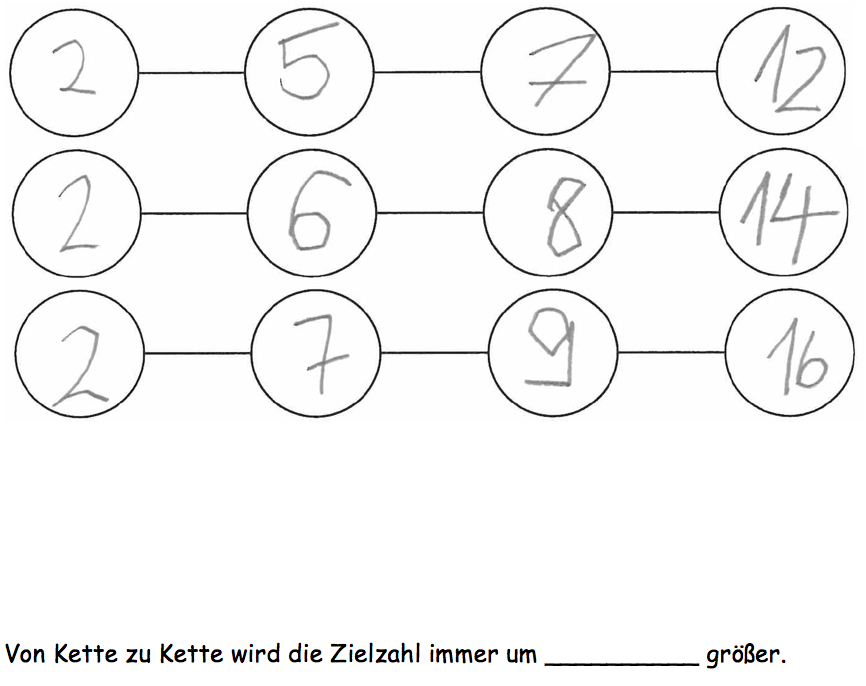
- Welche mathematischen Regeln und Besonderheiten liegen dem Aufgabenformat Zahlenketten zugrunde?
- Warum lohnt sich ein genauerer Blick auf die mathematischen Strukturen vor allem auch für den Unterricht?
- Wie können die Zahlenketten im Unterricht genutzt werden?
