Einstieg

Zählen, ohne zu zählen

Die Aufgabe, mit vier verschiedenfarbigen Bausteinen zweistöckige Türme zu bauen, die alle unterschiedlich sind, kann von Kindern mit verschiedenen Strategien gelöst werden – wie die folgenden Beispiele zeigen. 

Türme bauen

Du hast vier Bausteine in verschiedenen Farben: blau, rot, grün und schwarz.

Wie viele verschiedene Möglichkeiten gibt es, zweistöckige Türme zu bauen? Wie kannst du diese geschickt finden? Scheibe so auf, dass andere sehen können, wie du vorgegangen bist.

 

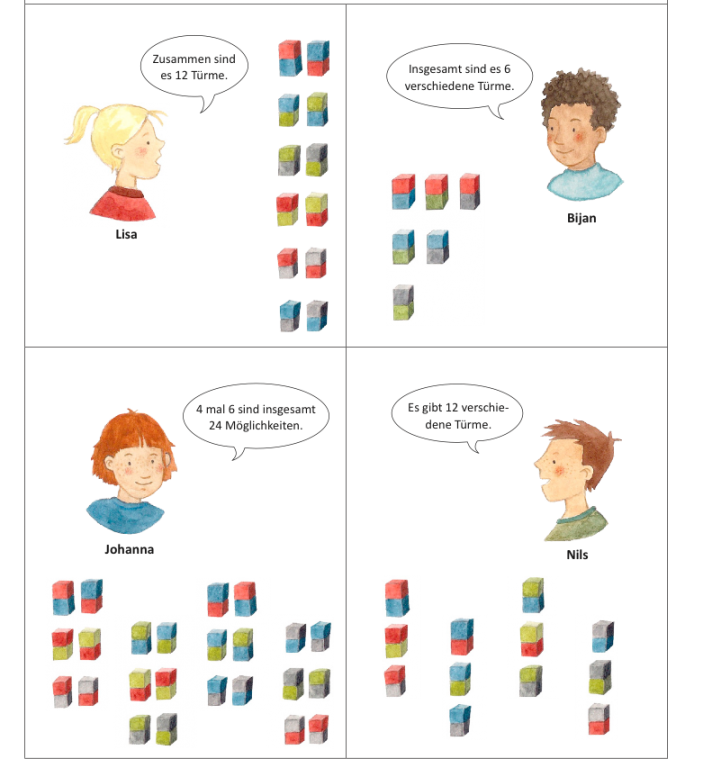
Anhand der unterschiedlichen, systematischen Vorgehensweisen der Kinder erkennt man gut, dass kombinatorische Aufgaben auch ohne komplizierte Rechenwege oder das Anwenden von Formeln lösbar sind. Zudem zeigt sich in den obigen Schülerlösungen eine Lösungsvielfalt, die auf unterschiedliche Herangehensweisen der Schüler schließen lässt.

Die (intensive) Betrachtung der mathematischen Struktur der Aufgabe hilft, bei solchen oder ähnlichen Aufgabenstellungen die individuellen Bearbeitungen der Schüler zu verstehen und deren Qualität möglichst umfassend bewerten zu können. Außerdem ist der mathematische Hintergrund wichtig, um auch Hilfestellungen anbieten, Fehlvorstellungen der Kinder aufbrechen und Vorstellungen aufbauen zu können. 

Auf den folgenden Seiten sollen sowohl die mathematischen Strukturen und Besonderheiten der Aufgabe „Türme bauen“ thematisiert als auch ein Überblick über mögliche systematische Strategien von Kindern gegeben werden.