Die Kombinatorik wird häufig als die Kunst des Zählens oder geschickten Zählens bezeichnet (vgl. Selter & Spiegel 2004, S. 295).
Dabei kann Unterricht unterschiedliche Schwerpunkte setzen. Je nach Schwerpunkt, variieren die Aufgabenstellungen des Unterrichts. Es können einerseits verschiedene Kombinationsmöglichkeiten im Vordergrund stehen („Welche Möglichkeiten gibt es?"), andererseits kann aber auch die Anzahl aller Möglichkeiten gesucht sein („Wie viele Möglichkeiten gibt es insgesamt?") (vgl. Kütting & Sauer 2008, S. 76).
Der Arbeitsauftrag „Wie viele verschiedene Möglichkeiten gibt es zweistöckige Türme zu bauen? Wie kannst du diese geschickt finden? Scheibe so auf, dass andere sehen können, wie du vorgegangen bist.“ soll die Kinder darin bestärken systematische Vorgehensweisen zu nutzen.
Im Folgenden soll vor allem der Frage nachgegangen werden, welche Strategien Schülerinnen und Schüler nutzen können, um alle unterschiedlichen Möglichkeiten zu bestimmen.
Warum sollte Kombinatorik als Thema schon in der Grundschule behandelt werden?
Die Bearbeitung kombinatorischer Aufgaben ist für ein späteres Verständnis solcher Aufgaben in Folgeschuljahren wichtig, wie u.a. Ruwisch betont: „Kombinatorische Aufgaben in der Grundschule leisten einen wichtigen vorbereitenden Beitrag, indem sie Grundschulkindern inhaltlich mit unterschiedlichen kombinatorischen Situationen vertraut machen und so einer sinnentleerten Anwendung kombinatorischer Formeln im weiteren schulischen Lernprozess vorbeugen“ (Ruwisch 2010a, S. 4).
Zudem bietet das Aufgabenformat zunächst einen leichten Einstieg, sodass alle Kinder schnell zu Lösungen kommen. Weiterhin wird an diesem Aufgabenformat sichtbar, wie eine Systematisierung auch einfacher Aufgaben (z.B. Finde alle zweistöckigen Türme!) die Grundlage liefert komplexere Aufgaben (z.B. Finde alle vierstöckigen Türme!) zu lösen.
Ein systematisches Vorgehen kann bei den Kindern nicht von Anfang an vorausgesetzt werden; vielmehr sollten Kinder immer wieder durch geeignete Aufgaben die Möglichkeit erhalten, ihre Vorgehensweisen zu erproben und zu erweitern. Hilfestellungen und vor allem gemeinsame Reflexionsphasen helfen den Schülerinnen und Schülern dabei, die individuellen Lösungswege zu strukturieren und die Lösungsvielfalt der Gruppe für den einzelnen Schüler wieder als Ausgangspunkt für weitere, eigene Erkundungen zu nutzen.
Und schließlich zeigt sich, dass kombinatorische Aufgabenstellungen sich zudem eignen, um prozessbezogene Kompetenzen zu fördern. Da Kindern (zunächst) keine Routinen bei der Bearbeitung kombinatorischer Aufgabenstellungen zur Verfügung stehen, eignen sie sich hervorragend für problemorientiertes Arbeiten (vgl. ebd.). (→ Problemlösen)
Kombinatorische Aufgaben sind zudem in den Bildungsstandards aufgeführt. Die Kinder sollten am Ende der vierten Jahrgangsstufe über Wissen in diesem Bereich verfügen. So ist unter der Leitidee „Zahlen und Operationen“ gefordert, dass Kinder „einfache kombinatorische Aufgaben (z.B. Knobelaufgaben) durch Probieren bzw. systematisches Vorgehen lösen“ (KMK 2004, S. 9) können.
Auf unserer Seite ,,Mathe mehr als rechnen" finden Sie weitere Informationen und Aufgabenbeispiele zu den einzelnen prozessbezogenen Kompetenzen.
Eigenaktivität
Überlegen Sie zunächst selbst: Worin besteht der Unterschied zwischen diesen beiden Problemstellungen?
Situation 1: Kastanien zählen

Situation 2: Türme bauen

Kombinatorische Aufgabenstellungen unterscheiden sich in drei wesentlichen Punkten von den bereits bekannten Aufgaben zur Anzahlbestimmung (vgl. Höveler 2014):
-
Während bei der ersten Situation die Anzahl der einzelnen vorliegenden Elemente gefragt ist, soll bei der zweiten (kombinatorischen) Situation eine Anzahl von Figuren, hier also von Türmen – bestehend aus immer zwei verschiedenfarbigen Bausteinen – gezählt werden.
-
Dabei liegen in Situation 1 (Kastanien) alle zu zählenden Elemente direkt vor. In Situation 2 müssen die Figuren (Türme) hingegen erst aus den zur Verfügung stehenden Elementen (vier verschiedenfarbige Bausteine) sukzessive hergestellt werden. Auf diese Weise entstehen demnach 12 verschiedene zweistöckige Türme.
-
In Aufgaben wie in Situation 1 ist das Ziel folglich immer, die Anzahl der Elemente direkt zählend zu bestimmen. In Situation 2 hingegen können die Bedingungen auch variieren. Da im gegebenen Beispiel jeder Baustein nur einmal vorliegt, kann eine Farbe nicht mit sich selbst kombiniert werden. Es kann also z. B. keinen zweistöckigen Turm bestehend aus zwei blauen Bausteinen geben. Wäre dies allerdings möglich, so müsste eben anders gezählt und kombiniert werden und weitere Lösungen wären demnach denkbar.
Mathematisch handelt es sich dabei um die kombinatorische Grundfigur der sogenannten Variation ohne Wiederholung. Konkret bedeutet dies hier:
Hier hast du vier Bausteine in verschiedenen Farben: grün, rot, schwarz und blau.
Wie viele verschiedene Möglichkeiten gibt es, zweistöckige Türme zu bauen? Wie kannst du diese geschickt finden? Scheibe so auf, dass andere sehen können, wie du vorgegangen bist.
Durch die Frage „Wie viele verschiedene Möglichkeiten gibt es, zweistöckige Türme zu bauen?“ sollen die Kinder an kombinatorische Anzahlbestimmungen herangeführt werden. Im Gegensatz zu der Frage „Welche Türme kannst du finden?“ zielt die obige Fragestellung eher darauf ab, dass die Kinder nicht immer alle Möglichkeiten aufschreiben oder aufmalen sollen, sondern im Laufe der Unterrichtseinheiten vielmehr systematische Strategien zum Bestimmen der Anzahl aller Möglichkeiten aus- und weiterbilden sollen. Welche Strategien genutzt werden können, wird im Folgenden – auszugsweise – beschrieben.
Welche Strategien nutzen die Kinder zur Bestimmung aller verschiedener Türme?
Im Folgenden stellen wir anhand der Turmaufgabe verschiedene Schülerstrategien vor.
Systematisch probieren
Diese Aufgabe kann probierend und zunehmend systematisierend gelöst werden. Nicht jedes Kind wird von Anfang an eine erkennbare Strategie verfolgen und systematisch alles aufschreiben. Dennoch gilt: „Die Schülerinnen und Schüler werden herausgefordert, eigene Lösungsansätze zu entwickeln. Da jeweils die Vollständigkeit der gesuchten Möglichkeiten nachzuweisen ist, zwingen kombinatorische Fragestellungen geradezu, systematisch vorzugehen, um den Überblick zu behalten“ (Ruwisch, 2010a, S. 4).
Das Systematisieren und Strukturieren der Lösungen ist somit auch ein wichtiger Teilaspekt für den eigenen Unterricht und wird im Unterricht noch genauer thematisiert.
Zunächst sollen Strukturierungsstrategien von Schülerinnen und Schülern im Allgemeinen erläutert werden, um nachvollziehen zu können, was mögliche Denkwege und Herangehensweisen der Kinder sein können.
Teilerfremde Paarbildung


So könnten die Kinder beispielsweise versuchen, mithilfe der sogenannten teilerfremden Paarbildung zu arbeiten. Das heißt, sie bauen zunächst Türme, bei denen keine Farbe gleich ist.
Gerade, wenn man bei vier Bausteinen und Zweiertürmen mit Material arbeitet, bietet sich diese Strategie zum Auffinden erster Lösungen an. Die Kinder bauen zunächst zwei Bausteine zusammen (z.B. blau und schwarz). Die beiden nicht verwendeten Steine (rot und grün) werden nun anschließend auch zu einem weiteren Turm zusammengesetzt. Nachfolgend werden beispielweise blau und grün miteinander verbaut und somit dann auch rot und schwarz zusammengesetzt.
Gegenpaarbildung
Zudem haben die Schülerinnen und Schüler mit der Gegenpaarbildung (vgl. Hoffmann 2003) auch eine Möglichkeit, Strukturen in den Lösungen zu entdecken. So kann beispielsweise ein gefundener Turm einfach „umgedreht“ werden.
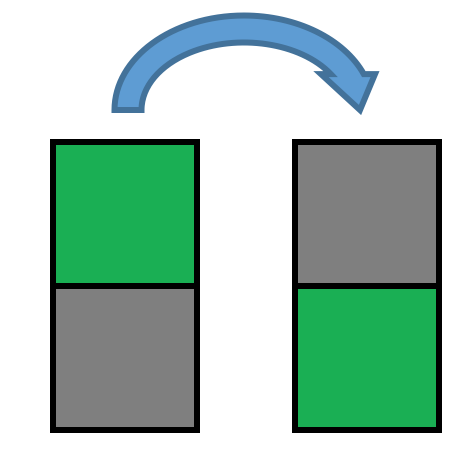
So entsteht ein weiterer Turm mit denselben Farben.
Sind mehr als zweistöckige Türme gesucht, funktioniert die Gegenpaarbildung immer noch, wird aber komplexer. Es ist eine Vorgehensweise „die darauf ausgerichtet ist, jeden neuen Turm in der Weise zu gestalten, dass alle Farben eine andere Position haben als im vorherigen Turm“ (Hoffmann 2003, S. 187).
Elementfixierung
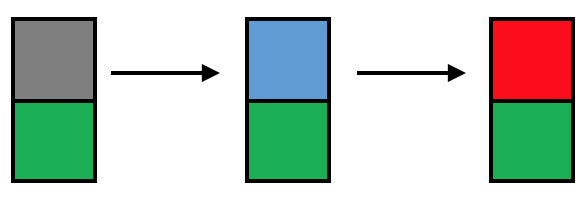
Eine weitere denkbare Strategie ist die sog. „Elementfixierung“ (vgl. Höveler) Wie beim Baumdiagramm (siehe unten) können die Kinder einen Baustein festlegen und dann die andere Position (bzw. die anderen Positionen) durchwechseln. Ein Element wird also fixiert.
Systematisch wird die verbleibende Position mit allen anderen Möglichkeiten besetzt. Besteht der Turm aus mehr als zwei Steinen, so wird beispielsweise zunächst der unterste fixiert – z. B. mit schwarz – dann der darunter – mit grün – und die verbleibenden Farben werden für die dritte Position verändert. Dann verändert man zunächst den zweiten Stein (also dieser ist beispielsweise nicht mehr grün, sondern blau) und überlegt dann, die wieder der letzte Stein besetzt werden kann.
Diese Strategien müssen auch nicht von Anfang an genutzt werden. Durch eine Aufforderung zum Sortieren der bisher gefundenen Lösungen können die Kinder dazu angeregt werden, ihr Überlegungen ordnen. Dies hilft den Kindern weitere Lösungen zu finden und doppelte Lösungen zu streichen. Dabei kann es auch sinnvoll sein, verschiedene Strategien miteinander zu verbinden, um sicher zu gehen, dass wirklich alle Möglichkeiten gefunden worden sind.
Nachdem gegen Ende einer solchen Unterrichtseinheit das Finden der Möglichkeiten nicht mehr im Vordergrund steht, können die Kinder versuchen, die Anzahl möglicher Türme auch durch Zählstrategien und ohne das Auflisten aller einzelnen Möglichkeiten zu bestimmen. So kann den Kindern beispielsweise auffallen, dass es für vier Farben und zweistöckige Türme 4 · 3 Möglichkeiten gibt, da sie einen Stein fixiert haben und feststellen, dass es zu jeder der vier Fixierungsmöglichkeiten drei verschiedene Türme gibt.
Ähnliche Lösungsstrategien sind für weitere kombinatorische Aufgaben möglich. Variationen und andere Fragestellungen werden im Unterrichtsteil kurz vorgestellt.
Welche mathematischen Strukturen und Besonderheiten stecken hinter der Turmaufgabe?
Durch das Auflisten aller möglichen Türme lässt sich die Anzahl bestimmen. Bei Zweiertürmen aus vier verschiedenen Farben lassen sich demnach die folgenden 12 unterschiedlichen Türme herstellen:

Wie bereits erläutert gibt es unterschiedliche Strategien, um auf alle 12 Möglichkeiten zu kommen. Bei der gegebenen Aufgabe ist das Notieren aller 12 Möglichkeiten noch (halbwegs) übersichtlich möglich. Bei wachsenden Zahlenwerten (z.B. mehr als vier Farben und/oder Türmen mit mehr als zwei Bausteinen) wird eine solche Auflistung jedoch nicht nur sehr schnell unübersichtlich, sondern auch immens zeitintensiv.
Aber wie kommt überhaupt schnell zu einer Lösung, ohne gleich alle Lösungen aufzuschreiben und anschließend abzuzählen?
„Genau genommen wird hier nicht gezählt, sondern (multiplikativ) gerechnet“ (Padberg & Büchter 2015, S. 243). Das soll im Folgenden genauer betrachtet werden.
Dazu kann folgendes überlegt werden:
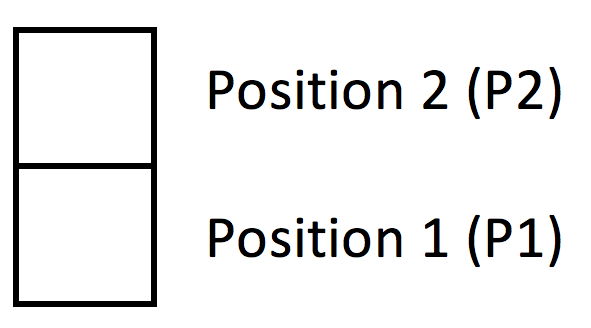
Im Beispiel besteht der Turm aus zwei Bausteinen. Es gibt also zwei Positionen, aus denen der Turm besteht. Der untere Baustein wird von nun an als Position 1 (P1), der obere als Position 2 (P2) bezeichnet. Wenn später höhere Türme thematisiert werden, können beliebig viele Stockwerte – und somit auch Positionen – entsprechend nach oben durchnummeriert werden.
Da es vier verschiedene Bausteine gibt, hat man für die erste Position vier Möglichkeiten einen Baustein für diese Position auszuwählen.
Angenommen für Position 1 wurde der schwarze Baustein ausgewählt (siehe Grafik):
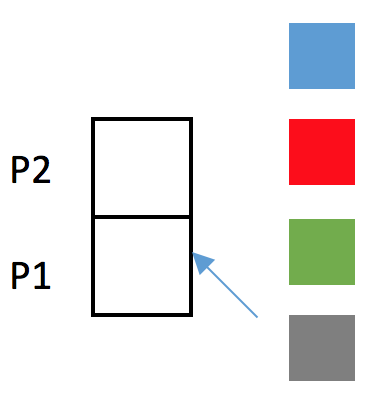
Da der schwarze Baustein nun bereits an Position 1 steht, steht er für die zweite Position nicht mehr zur Verfügung. Es verbleiben für die zweite Position also nur noch drei Möglichkeiten den Turm zu vervollständigen, nämlich die dreiübrig gebliebenen Bausteine.
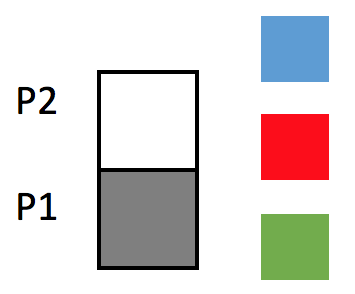
Für Position 1 hat man also zu Beginn noch alle vier unterschiedlichen Möglichkeiten einen Baustein auszuwählen. Ist diese Auswahl getroffen, so verbleiben für Position 2 noch genau drei Möglichkeiten, da ein Baustein ja bereits auf Position 1 verbaut wurde.
Folglich gibt es insgesamt 4·3 Möglichkeiten aus vier verschiedenfarbigen Bausteinen einen zweistöckigen Turm zu bauen.
Dies lässt sich auch gut anhand eines Baumdiagramms verdeutlichen:
Alle möglichen Türme im Überblick
Jeweils drei verbleibende Möglichkeiten für Position 2
Zu Beginn vier Möglichkeiten für Position 1
Eigenaktivität
a) Wie viele Lösungen finden Sie, wenn Sie aus den gegeben vier Bausteinen nun einen dreistöckigen Turm bauen sollen?
b) Wie viele Lösungen finden Sie, wenn sich alle Bausteine beliebig oft wiederholen dürfen für zweistöckige bzw. dreistöckige Türme?