Farbige Türme bauen
Wie kann man im Unterricht sinnvoll mit den systematischen Strategien der Kinder weiterarbeiten?
Das übergeordnete Ziel der Unterrichtseinheit ist das Sammeln von Erfahrungen mit der Bestimmung kombinatorischer Anzahlen und das Verinnerlichen der Notwendigkeit eines strukturierten Vorgehens.
Dabei steht das geschickte Finden aller Möglichkeiten, also die Strategien im Vordergrund. Zunächst liegt der Fokus ebenso auf der Dokumentation dieser Strategien, denn so werden die Unterschiede im Vorgehen sichtbar. Ausgehend von der Dokumentation können die Strategien der Kinder weiterentwickelt werden.
Die im Folgenden dargestellte Unterrichtsreihe wird in drei Einheiten unterteilt.
In jeder der drei Phasen wird ein wichtiges Lernziel verfolgt, an das anschließend angeknüpft werden soll. Die übergeordnete Fragestellung dabei ist immer: Wie finde ich geschickt alle möglichen Türme?
Türme finden - Wie viele können wir bauen?
Die Unterrichtseinheit beginnt mit der Problemstellung, die Anzahl aller verschiedener Zweiertürme aus vier verschiedenfarbenen Bausteinen zu bestimmen.
Dabei können die Kinder mit Hilfe von Material zunächst selbst versuchen, die verschiedenen Türme zu bauen, und die gefundenen Möglichkeiten dokumentieren.
Oder, ohne zur Hilfenahme mit Material gefundene Türme (zeichnerisch) dokumentieren.
Bei kombinatorischen Anzahlbestimmungsproblemen zeigen Kinder (im Unterricht) in der Regel unterschiedliche Herangehensweisen und Strategien.
Die Kinder werden unterschiedliche Strukturierungsarten finden und dabei
-
einige, aber noch nicht alle Möglichkeiten finden, oder zu viele
-
durch strukturiertes Vorgehen bereits alle Möglichkeiten finden und
-
darüber hinaus die dahinterliegende mathematische Struktur erkennen.
Es gehört dazu, dass manche Kinder zunächst probierend und unsystematisch an die Aufgaben herangehen. Probierende und unsystematische Strategien haben in dieser Phase ihre Berechtigung und bilden ebenso wie systematisches Vorgehen die Grundlage zur Weiterarbeit mit den Strategien der Kinder.
Gefundene Steine dokumentieren
Wichtig in dieser Unterrichtsphase ist die Dokumentation der gefundenen Türme, so behalten die Kinder einen Überblick über ihre Lösungen. Ebenso erhält die Lehrkraft einen guten Überblick über die verschiedenen Strategien der Kinder und kann passende Dokumente für die anschließende Unterrichtsphase auswählen.
Weiterhin hilft die Dokumentation in der folgenden Unterrichtsphase dabei, die Herangehensweisen einzelner Kinder miteinander zu vergleichen.
Die drei folgenden Schülerbeispiele zeigen exemplarisch die Vielfalt der Dokumentationsmöglichkeiten.
Während Lara (Abb.1) die verschiedenen Möglichkeiten aufzeichnet und dabei sieben verschiedene Türme entdeckt, findet Benjamin (Abb. 2) alle Türme. Er geht dabei systematisch vor und kürzt die Farben durch Buchstaben ab. Tim geht ebenfalls systematisch vor, jedoch findet er mit seiner Strategie nicht alle Türme (Abb. 3).
 Laras Lösung
Laras Lösung
 Benjamin findet alle
Benjamin findet alle
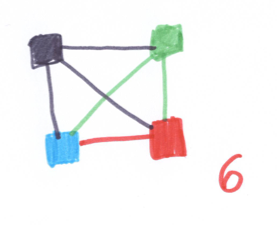 Tims Lösung
Tims Lösung
Knackpunkt bei den Aufgabenstellungen:
Für die Kinder wird in dieser Phase vermutlich die Frage: „Welche Türme kann ich bauen?“ im Vordergrund stehen.
In der Einstiegsphase ist diese Herangehensweise zunächst legitim, denn so können die Kinder sich langsam an die Aufgabenstellungen herantasten. Trotzdem ist es wichtig, mit den Kindern im Laufe der Unterrichtseinheit zu besprechen, dass es (bei dieser Art von Aufgaben) darauf ankommt, geschickt, also systematisch alle Möglichkeiten zu finden.
Im Gegensatz zu anderen Aufgaben, z.B. finde Plusaufgaben mit dem Ergebnis 20, ist bei kombinatorischen Anzahlbestimmungen, die Frage nach ALLEN Möglichkeiten unabdingbar.
Unterrichspraktischer Hinweis:
Als Material eignen sich z.B. Steckwürfel. Diese sind in den meisten Schulen vorhanden und die Kinder sind daher mit ihnen bereits vertraut. Alternativ können auch Legosteine genutzt werden.
Systematisieren - Wie haben wir alle gefunden?
Nach der Bau- und Dokumentationsphase können die Kinder in Partner- oder Kleingruppenarbeit ihre Ergebnisse miteinander vergleichen und sich über ihre Herangehensweisen austauschen und dabei die Frage beantworten, wie sie alle Lösungen gefunden haben.
Das ist zunächst einmal eine zweiteilige Aufgabe, zunächst müssen die Kinder alle Türme finden, um dann mit zweiten Schritt zu formulieren, warum es nicht mehr Türme geben kann.
Für die erste Reflexionsphase erhalten die Kinder also den Auftrag, ihre individuellen Lösungswege zu strukturieren. Die Ergebnisse sollen in einem Protokoll festhalten werden.
-
Vergleicht eure Ergebnisse miteinander.
-
Wie viele Möglichkeiten gibt es insgesamt? Zeichne alle Möglichkeiten geordnet auf.
-
Wie bist du vorgegangen? Warum ist deine Strategie besonders geschickt? Findest du einen Namen für deine Strategie?
Um zu überprüfen, ob alle Türme gefunden wurden, ist es sinnvoll, die bereits gefundenen Türme zu sortieren. Kinder, die bisher nur probierend Lösungen gefunden haben, lernen die Strategien der anderen Kinder kennen und können so eventuell noch weitere Türme finden.
Der zweite Teil des Arbeitsauftrages (Frage 2) gibt implizit Hilfestellung, für die Kinder, die noch nicht alle Möglichkeiten gefunden haben, denn werden die gefundenen Türme zunächst sortiert, lassen sich fehlende Türme leichter finden. Welche Möglichkeiten habe ich schon? Wie kann ich meine Lösungen sortieren? (vgl. Beispiel Lara)
 Gefundene Lösungen erweitern
Gefundene Lösungen erweitern
Lara nimmt den Impuls auf, ihre Türme zu sortieren. Dabei gruppiert sie zunächst alle Türme die den gleichen oberen Baustein haben.
Ihr fällt auf, dass sie mit Grün oben nur einen Turm gefunden hat. Den doppelt gefundenen dreht sie um. Anschließend ergänzt sie systematisch die Türme, die ihr noch fehlen.
Vorgehensweisen beschreiben
Nachdem alle Türme gefunden wurden, geht es im nächsten Schritt darum, den Fokus auf die Strategien zu lenken (Frage 3). Wie Sie im Hintergrund bereits kennengelernt haben, gibt es unterschiedliche Strategien, alle Zweiertürme zu finden.
Die Kombinatorik ist „die Kunst des geschickten Zählens“, das bedeutet also konkret, dass der Fokus auf die Struktur und den Prozess des geschickten Findens gerichtet wird.
Um im Anschluss den Prozess des Findens zu beschreiben, ist die Dokumentation der gefundenen Türme eine geeignete Grundlage. Weiterhin kann die Lehrkraft leicht nachvollziehen, ob eher probierend oder bereits (zunehmend) systematisch vorgegangen wurde.
Eigenaktivität
Lara hat in der Einzelarbeit folgende Türme gefunden und bringt ihre dokumentierte Lösung mit in die Kleingruppe. Überlegen Sie, wie Lara vorgegangen sein könnte.

Den Strategien Namen geben
Um den Fokus auf die Strategie zu lenken, ist es hilfreich, die Strategien mit einem Namen zu bezeichnen. Dann lässt sich im weiteren Verlauf des Unterrichts leichter über die Strategien sprechen.
In der Plenumsphase ist es notwendig, dass die Lehrkraft viele verschiedene Kinder ihre Strategie vorstellen lässt, sodass ein breites Feld an möglichen Strategien zur Lösungsfindung besprochen werden kann. Dabei „sollten die von den Lernenden entwickelten Strategien nicht als falsch eingestuft und verworfen werden, sondern vielmehr als Ausgangspunkt für die Thematisierung von Strategien eingesetzt werden.“ (Höveler 2016, S. 317).
Die Namen können mit den Kindern gemeinsam gefunden werden. Wichtig bei der Namenswahl ist, dass das wesentliche Merkmal benannt wird. Die Strategie der Einzelvertauschung bezeichnen die Kinder hier mit Türme umdrehen. Das Tachometerprinzip, welches Nils nutzt, kann beispielsweise ein Stein bleibt fest genannt werden.
Knackpunkt:
Für die Weiterentwicklung der Strategien im Unterrichtsgespräch ist es wichtig, die wesentlichen Merkmale der Strategie herauszuarbeiten. Im Folgenden beschreiben drei Kinder ihre Herangehensweisen. Überlegen Sie, welches jeweils ein zentraler Anhaltspunkt für das Strategiemerkmal ist.
Nils und Lisa wenden je eine sich ebenfalls unterscheidende Strategien an.
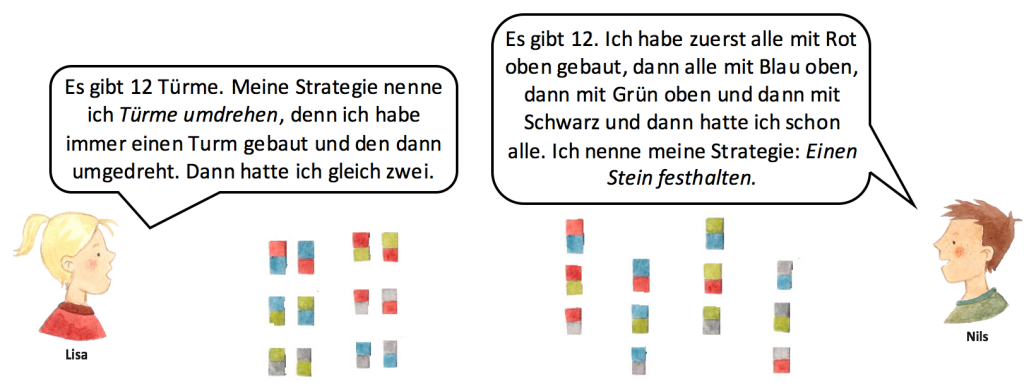
Lisa hat zwar alle Möglichkeiten gefunden, allerdings führt ihre Strategie: Türme umdrehen nicht notwendigerweise immer zu allen Möglichkeiten. Nils geht ebenfalls systematisch vor. Er wählt jeweils eine Farbe, hält den Stein fest und baut die drei Türme mit den anderen drei Farben.

Johanna mischt beide Strategien: Scheinbar startet sie mit der Strategie Ein Stein bleibt fest, sie wählt je eine Farbe und baut alle Variationen. Dann dreht sie jeden Turm der gesamten Gruppe um, sie nutzt also ebenfalls die Strategie Türme umdrehen. Johanna findet mit ihrer Strategie jedoch zu viele Möglichkeiten.
Im weiteren Unterrichtsverlauf kommt es nun darauf an, die Strategien der Kinder immer wieder aufzugreifen und weiterzuentwickeln.
Strategien besprechen – Warum haben wir alle?
In dieser Unterrichtsphase geht es darum, über die gefundenen Strategien zu reflektieren und daran anknüpfend zu begründen, dass alle Türme gefunden wurden. Diese Phase bietet die Grundlage für die Möglichkeit die Strategien zu verallgemeinern, bzw. auf andere Problemstellungen anzuwenden.
Beschreiben von Vorgehensweisen
An dieser Stelle werden die Lösungen von Lara und Johanna noch einmal aufgegriffen. Nachdem Lara ihre Türme nach Farben sortiert hatte, konnte sie systematisch die fehlenden Möglichkeiten ergänzen. Johanna hat ihre Türme ebenfalls nach Farben sortiert und dabei alle Lösungen gefunden, jedoch strategiebedingt alle Lösungen doppelt gezählt. Ein mögliches Unterrichtsgespräch kann durch einen Vergleich von zwei Strategien angeregt werden.
Eigenaktivität
Vergleichen Sie zunächst einmal selbst: Welche Gemeinsamkeiten finden Sie in den Strategien der beiden? Worin unterscheidet sich ihr Vorgehen?
 Lara
Lara
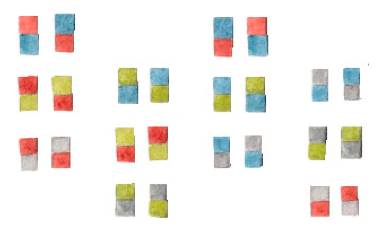 Johanna
Johanna
Um zu beweisen, dass keine Möglichkeiten vergessen und keine doppelt gezählt wurden, reicht folglich das systematische Aufschreiben alleine noch nicht aus. Um das doppelte Aufschreiben einzelner Kombinationen auszuschließen, muss die kombinatorische Grundfigur erkannt werden. Für die vorliegende Aufgabe bietet sich das Baumdiagramm als Strukturierungshilfe an, denn daraus lässt sich die multiplikative Struktur der Aufgabe abgelesen und weitergedacht werden.
Mit den Kindern sukzessive ein Baumdiagramm entwickeln
Um mit den Kindern das Baumdiagramm als Darstellungsoption zu entwickeln, kann z.B. Tims Lösungsstrategie als Impuls dienen. Falls in Ihrer Klasse kein Kind eine solche oder ähnliche Lösung entwickelt hat, ist Tims Lösung als fiktives Schülerdokument nutzbar (Material).
Schau mal, das ist Tims Lösung. Was meinst du, wie er vorgegangen ist? Hat er alle Lösungen gefunden? Warum, warum nicht?
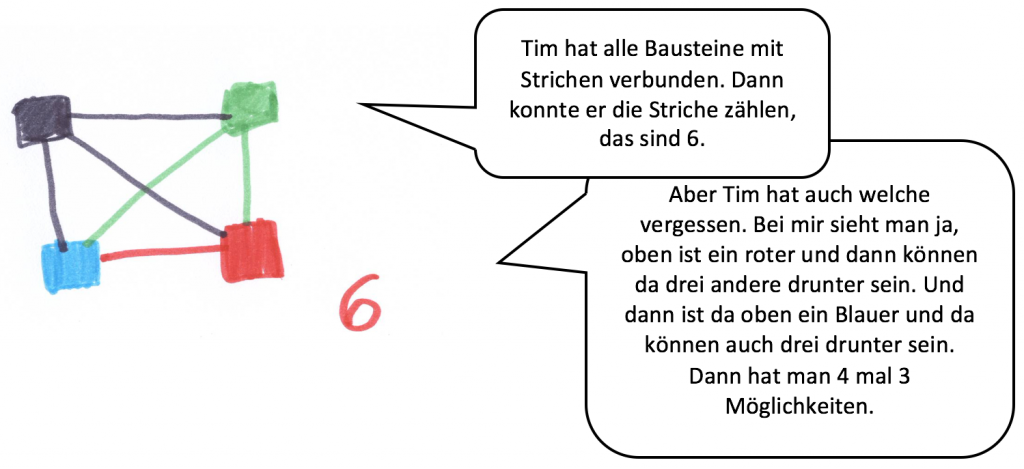
Nachdem Lara zunächst Tims Strategie beschreibt, vergleicht sie ihre Lösung mit seiner. Im weiteren Verlauf nutzt sie Tims Vorgehensweise, um ihre Türme noch einmal anders zu strukturieren (Abb. 7). An dieser Stelle sind die wesentlichen Elemente eines Baumdiagramms bereits erarbeitet. In einem nächsten Schritt zeigt die Lehrerin an der Tafel, oder mit Hilfe von Laras Teilbäumen, wie ein Mathematiker diese Lösungen aufschreibt (Abb. 8).
 Lara greift Tims Strategie auf
Lara greift Tims Strategie auf
 Baumdiagramm aus Laras Teilbäumen
Baumdiagramm aus Laras Teilbäumen
Warum bist du dir sicher, dass du alle möglichen Türme gefunden hast? Warum gibt es nicht noch mehr Türme?
An dieser Stelle im Unterricht haben die Kinder gesehen, wie mit Hilfe eines Baumdiagramm die gefundenen Lösungen strukturiert aufgeschrieben werden können.
Im zweiten Schritt geht es um eine Begründung. Dabei kann die Diskussionen durch die Leitfrage: „Wie können wir sicher sein, dass wir keinen Turm vergessen haben?“ angestoßen werden. Eine mögliche Schülerantwort formuliert Lara und trifft dabei den Kern der Begründung schon gut. Sie bleibt dabei zwar noch auf der exemplarischen Begründungsebene, formuliert aber im Ansatz schon Verallgemeinerungen.

Welche ähnlichen (gegebenenfalls auch weiterführenden) Aufgaben sind denkbar?
Um Kinder anzuregen, ihre Strategien so (weiter) zu entwickeln, dass sie die Anzahl der Lösungen nicht mehr nur durch das einzelne Aufschreiben aller Möglichkeiten bestimmen können, können im Laufe der Grundschulzeit ähnliche Aufgaben gewählt werden.
Dazu sind verschiedene Aufgabenstellungen im Kontext „Türme bauen“ denkbar. Unterschiedliche Teile der Aufgabenstellungen können dabei variiert werden. Denkbar ist, die Anzahl der Farben oder auch die Stockwerkanzahl zu erhöhen, wie schon in der Eugenaktivität im Hintergrund. Möglich wäre auch, dass Wiederholungen derselben Farbe innerhalb eines Turmes zugelassen werden, indem man nun für jeden Turm mehrere Steine einer Farbe zur Verfügung hat.
Folgende mögliche Variationen der Aufgabenstellung sind denkbar:
-
Variation ohne Wiederholung
Stockwerk erhöhen
,,Hier hast du vier Bausteine in verschiedenen Farben: grün, rot, schwarz und blau. Wie viele verschiedene dreistöckige Türme kannst du daraus bauen?''
-
Variation ohne Wiederholung
Anzahl der farbigen Würfel erhöhen
,,Hier hast du 6 Bausteine in den verschiedenen Farben: grün, rot, schwarz, blau, gelb und weiß. Wie viele verschiedene zweistöckige Türme kannst du daraus bauen?''
-
Variation mit Wiederholung
doppelte Farben zulassen

,,Hier hast du blaue und rote Bausteine. Wie viele vierstöckige Türme kannst du bauen?''
Knackpunkt:
Die jeweiligen Varianten können natürlich miteinander kombiniert werden, sodass man etwa gleichzeitig die Anzahl der Farben und die Anzahl der Stockwerke erhöht. Dabei sollten Sie aber stets darauf achten, dass die Anzahl der Möglichkeiten nicht zu groß wird. Überlegen Sie also vorher selbst, wie viele Möglichkeiten es geben kann.
Weitere Aufgabenkontexte
Nicht nur der Kontext „bunte Türme“ lässt sich nutzen, um kombinatorische Aufgaben (im Bereich der Variation) zu bearbeiten. So sind u.a. auch die folgenden Materialien und Kontexte denkbar, um kombinatorische Aufgabenstellungen zu bearbeiten:
-
Vier Kinder sollen sich auf alle unterschiedliche Weisen vor der Tür aufstellen (vgl. Stoye 2010).
-
Die sogenannten Strummitierchen: Vier Bausteine werden zu Strummitierchen zusammengebaut (vgl. Steinau 2010).
-
Alle möglichen vierstelligen Zahlen aus den Ziffern 1, 2, 3 und 4 herstellen.
-
Alle möglichen vierstelligen Zahlen aus den Ziffer 1, 2, 3, 4 und 5 herstellen.
-
Drei verschiedene Tiere jeweils in Beine, Rumpf und Kopf aufteilen und diese wieder zusammenbauen, sodass lustige Tiermischungen entstehen (vgl. Baumann & Koch 2011 (Grundschulunterricht)).
-
5 Teilnehmer laufen um die Wette. Wie viele Möglichkeiten gibt es für die Besetzung der ersten drei Plätze?
-
Eine Gruppe von Kindern, z.B. 6 will sich für ein Foto in eine Stuhlreihe setzen. Wie viele verschiedene Möglichkeiten zur Anordnung gibt es?
-
Es soll eine Kette aus Perlen gebastelt werden. Die Anzahl der Perlen auf der Kette kann variieren, genauso wie die Anzahl der Farben. Oder die Möglichkeit, ob die Farben wiederholt werden können.
-
...