Mathematische Besonderheiten und Strukturen
Die Zahlenmauer ist ein Übungs- und Aufgabenformat, welches sich im Mathematikunterricht sehr bewährt hat – nicht zuletzt, weil es zahlreiche Entdeckungen über Muster und Strukturen (vgl. Mathe – mehr als rechnen) zulässt. Um das Potential dieses Aufgabenformats ausnutzen zu können, ist es wichtig, dass man als Lehrkraft die besonderen mathematischen Strukturen durchdrungen hat.
Daher wird auf dieser Seite folgenden Fragen nachgegangen:
Wie ist eine Zahlenmauer aufgebaut?
Wie schon auf der Einstiegsseite beschrieben, ist eine Zahlenmauer so aufgebaut, dass auf je zwei benachbarte Steine einer Schicht ein dritter Stein gesetzt wird, in den die Summe der beiden unteren Steine einzutragen ist. Somit führt die Zahlenmauer A zu drei Additionsaufgaben, die Mauer B zu 3 Subtraktionsaufgaben und die Mauer C zu 2 Subtraktions- und einer Additionsaufgabe:
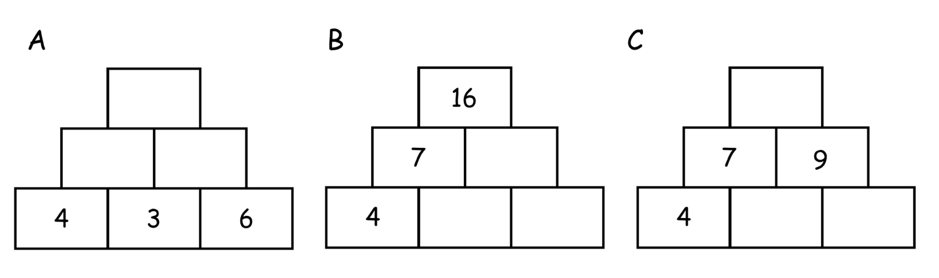
Durch den Aufbau der Zahlenmauern bereitet den Kindern die Mischung der Operationen weniger Probleme als beispielsweise gemischte Additions- und Subtraktionsaufgaben in Rechenpäckchen, da sie dort das Operationszeichen gerne mal übersehen. So ist den Kindern ein flexibles Wechseln zwischen den Operationen möglich – gerade die Zusammenhänge zwischen Addition und Subtraktion werden hierbei deutlich.
Durch einen Prüfstein bieten sich die Zahlenketten auch zur Selbstkontrolle an. Sie können ebenfalls problemlos erweitert werden, sodass sich schnell ein höherer Zahlenraum ergibt (vgl. Wittmann & Müller 1990).
Aber nicht nur auf dieser Ebene haben die Zahlenketten Potential. Aufgabenstellungen, die zu Entdeckungen bezüglich der Strukturen anleiten eignen sich in besonderer Weise auch zur Förderung der prozessbezogenen Kompetenzen (vgl. Mathe - mehr als Rechnen).
Eigenaktivität
Versuchen Sie bitte, die folgende Zahlenmauer zu lösen:
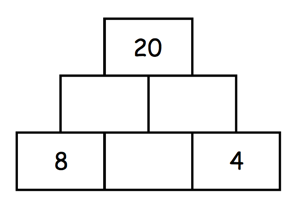Bildunterschrift
Und welche algebraische Struktur steckt in diesem Aufgabenformat?
Warum erhöht sich die Summe im Deckstein sich um 2, wenn die Zahl im mittleren Basisstein um eins erhöht wird? Um diese mathematischen Strukturen besser veranschaulichen zu können, stellen Sie sich vor, Sie haben ein grünes Säckchen, in welches Sie eine beliebige Anzahl an Plättchen packen können. Dieses legen Sie in den unteren linken Basisstein. Ein rotes Säckchen nehmen Sie für den mittleren Stein und einen blauen für den rechten.
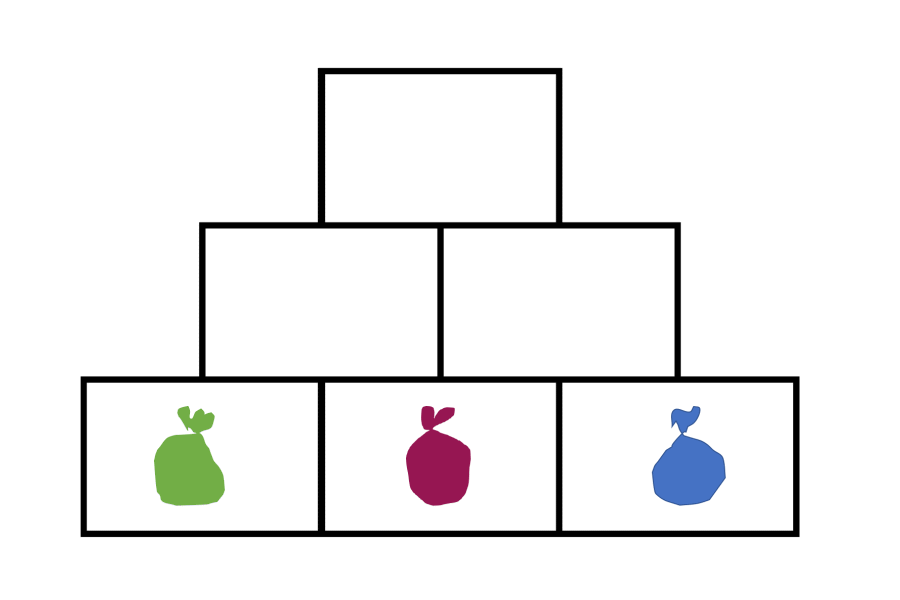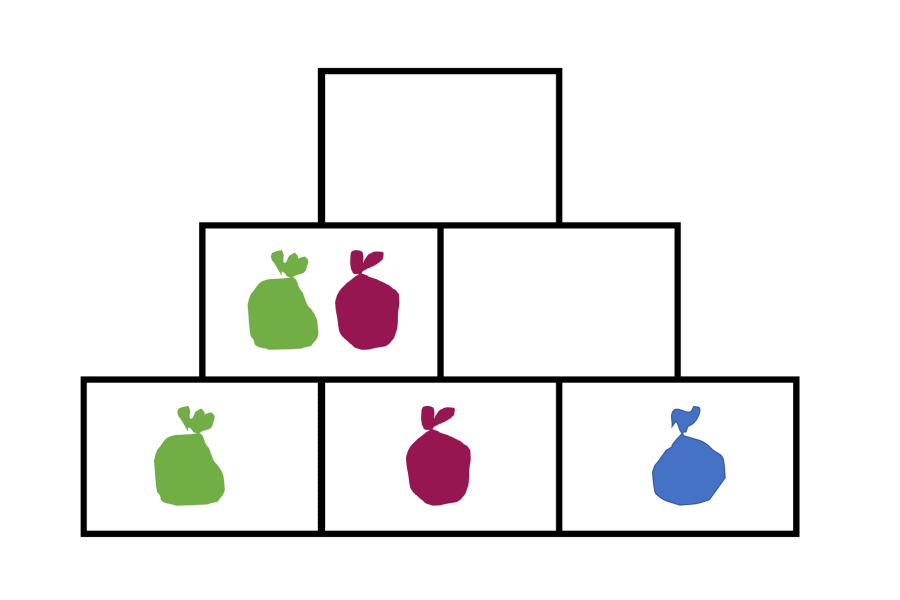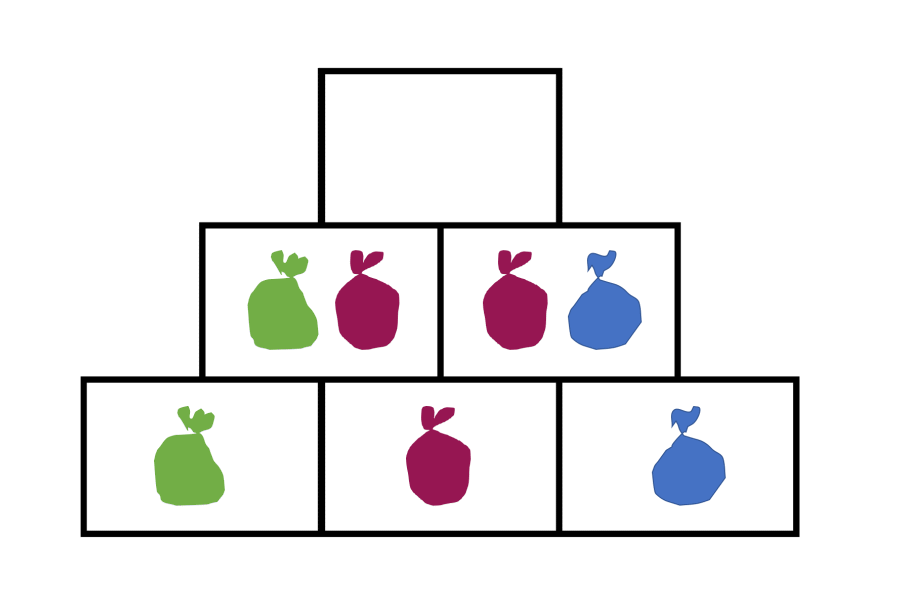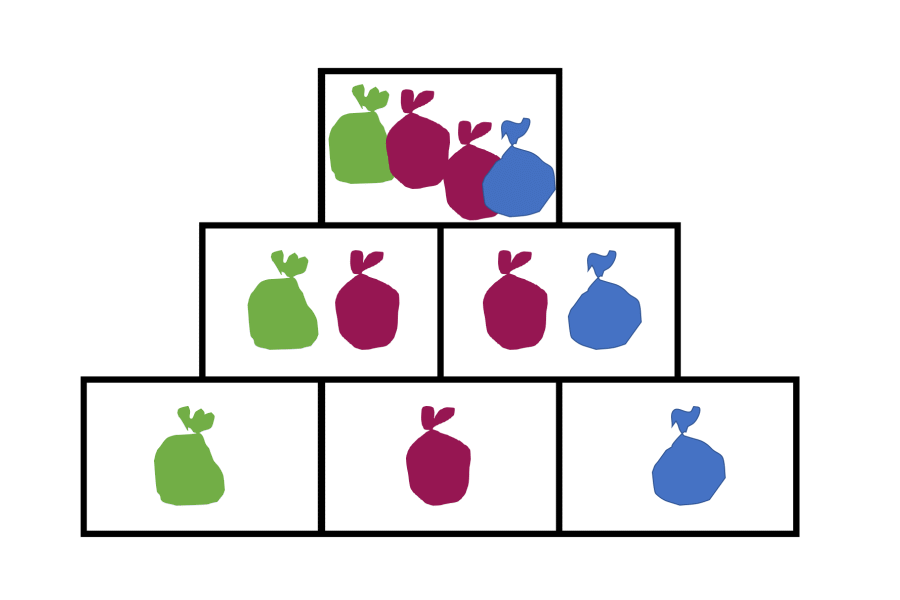
Dieser Zusammenhang wird ebenfalls deutlich, wenn man sich die algebraische Struktur einer Zahlenmauer ansieht. Dazu nutzt man nun – anstelle der Säckchen – Variablen, sprich a, b und c.
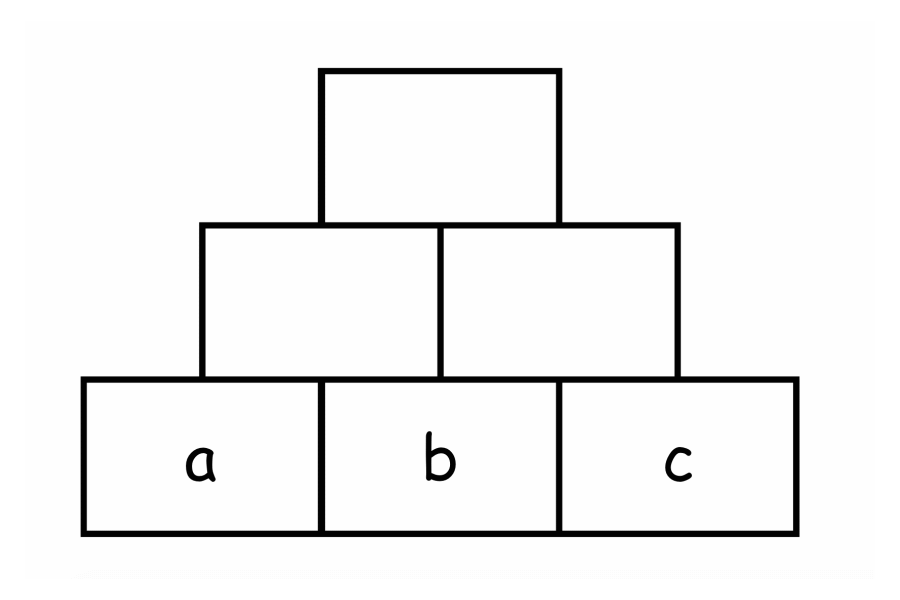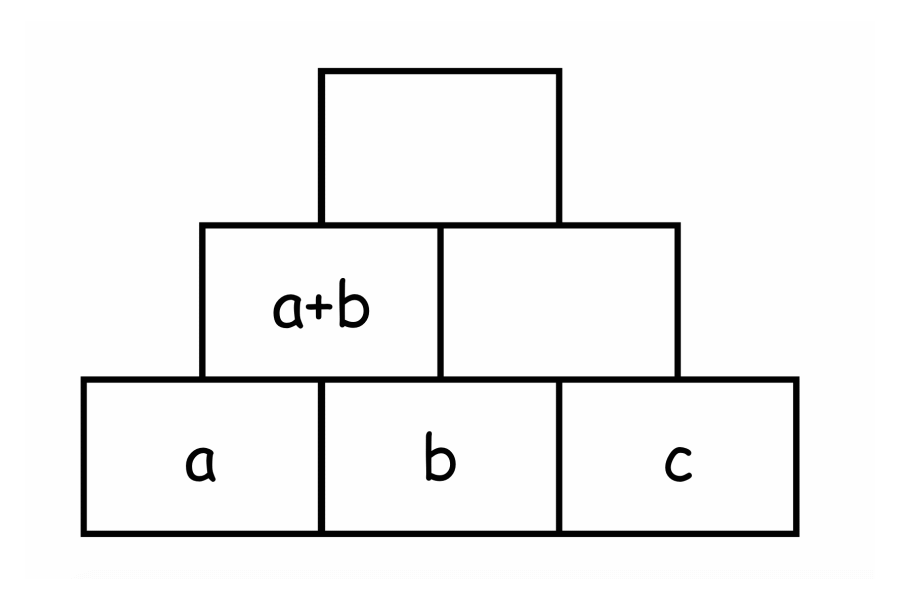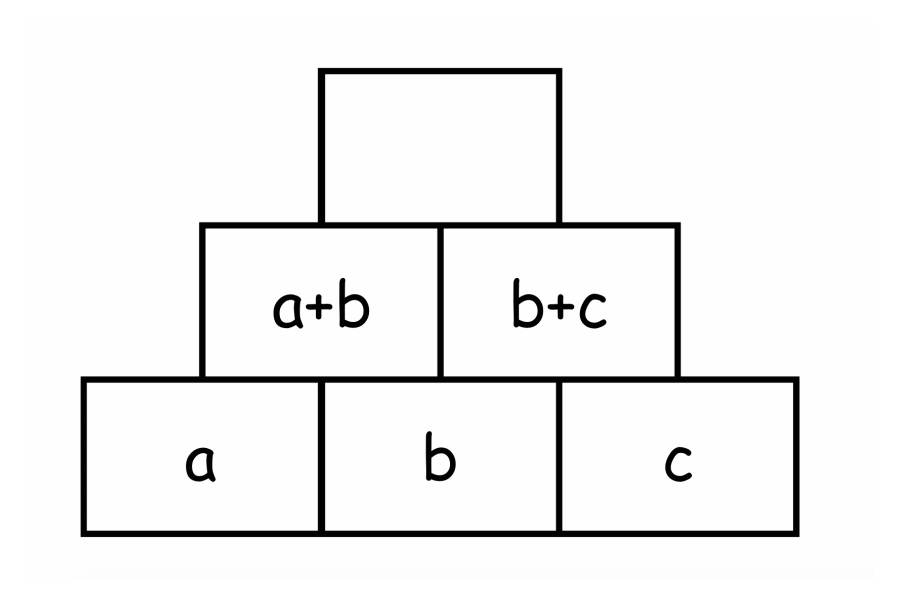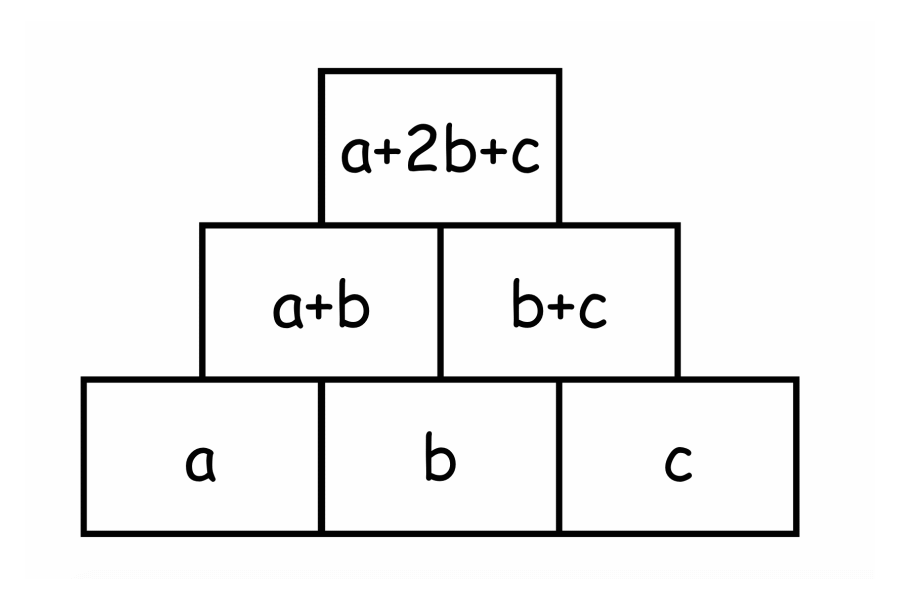
Man erkennt an beiden Darstellungen, dass der mittlere Basisstein zweimal in der Summe des Decksteins enthalten ist. Wird also der mittlere Basisstein um eins erhöht, erhöht sich die Summe im Deckstein um 2 – da der mittlere Basisstein sich zweifach auf den Deckstein auswirkt. Solche Entdeckungen können die Kinder – sicherlich aber auf ihrem Niveau und nicht mit Variablen – sehr gut tätigen, wenn sie dazu angeleitet werden.
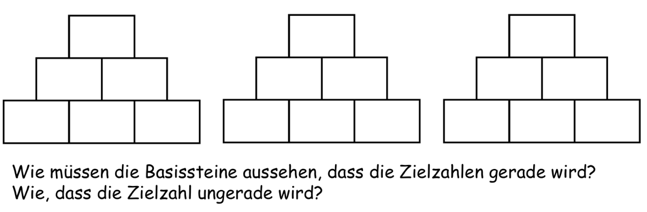
Mit diesem Wissen, denken Sie noch einmal an das Eingangsbeispiel aus einem Schulbuch zurück:
Eigenaktivität
Lösen Sie die Aufgabe! Argumentieren Sie nach Möglichkeit einmal grundschulgemäß und einmal algebraisch.
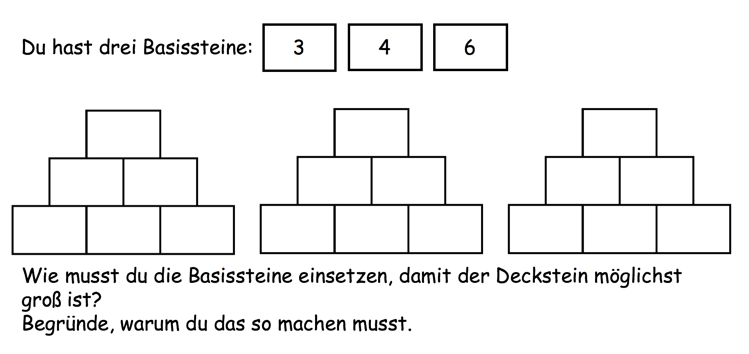
Sobald die mathematischen Strukturen hinter den Zahlenmauern durchdrungen worden sind, lassen sich zahlreiche ergiebige und differenzierte Aufgabenstellung im Kontext der Zahlenmauern finden. Da dieses Aufgabenformat solch zahlreichen Möglichkeiten bietet, sollte es nicht nur zur Festigung des Rechnens, also für die Förderung der inhaltlichen Kompetenzen genutzt werden. Vor allem zur Förderung der prozessbezogenen Kompetenzen bietet sich das Aufgabenformat folglich an.
Welche Übungen rund um das Aufgabenformat Zahlenmauern in der Grundschule möglich sind, erfahren Sie im Unterricht.
Welche Lernchancen stecken in diesem Aufgabenformat?
Die zahlreichen Gelegenheiten zum Üben der Grundrechenarten gemäß dem Prinzip des entdeckenden Lernens können hier nur durch einige Fragestellungen exemplarisch angedeutet werden.
Hingewiesen sei auf die unterschiedlichen Anspruchsniveaus, die zunächst einmal das ‚schlichte Ausfüllen' betreffen, sich dann aber insbesondere durch das Erkennen von Zusammenhängen ausdifferenzieren, sodass auch nach Erklärungen, Begründungen gefragt werden kann. Die Muster, die eine Zahlenmauer aufweist, eignen sich in besonderer Weise dazu Entdeckungen zu tätigen – die Kinder können also dazu angeregt werden, problemlösend vorzugehen, oder ihre Entdeckungen zu beschreiben und zu begründen, oder aber auch dazu, diese Entdeckungen darzustellen und darüber zu kommunizieren. Somit lassen sich je nach Aufgabenstellung unterschiedliche prozessbezogene Kompetenzen fördern.
Zudem wird durch das Aufgabenformat das sogenannte algebraische Denken gefördert.
Aus mehreren Gründen ist die Förderung des Weges hin zum verallgemeinerten Denken ab der Grundschule relevant: Neben dem vorbereitenden Charakter auf spätere Anforderungen in der Sekundarstufe liegen die Gründe aber vor allem im Mehrwert für die Kompetenzentwicklungen direkt in der Grundschule, um in Zusammenhängen zu denken und nicht nur anhand eines Zahlenbeispieles.
Arithmetische Kompetenzen werden durch mathematische Durchdringung gestärkt und unterstützt sowie Prozesskompetenzen, z. B. des Kommunizierens und Argumentierens, von algebraischen Denkweisen eingefordert und gefördert (Steinweg 2013).
Steinweg (2016) schlägt unter anderem diese zwei Grundideen vor, an denen sich die Förderung algebraischen Denkens – also dem Weg zu verallgemeinertem Denken – in der Grundschule orientieren kann. Diese lassen sich sehr gut mit Zahlenmauern verdeutlichen und fördern:
Muster zeigen sich als regelmäßige Wiederholungen von Zahlen oder geometrischen Objekten. Exemplarische Beispiele sind Muster in Zahlenmauern, die entdeckt, genutzt und auch beschrieben werden können.
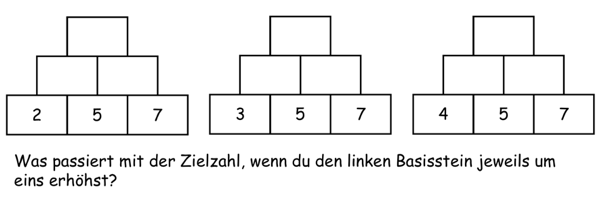
Im Gegensatz zu Mustern sind Eigenschaften ‚vorgegeben‘ (Wittmann & Müller 2007). Sie ergeben sich zwingend aus der algebraischen Struktur der Zahlenmauern. Die Aktivitäten im Unterricht entsprechen denen zu Mustern (entdecken, nutzen und beschreiben), betreffen nun aber die mathematischen Eigenschaften der Zahlen (z.B. Teilbarkeit).
Keine der Grundideen ist völlig unabhängig von bereits etablierten Unterrichtsinhalten, sondern fokussiert hingegen neu auf die Potenziale, die in den vermeintlich arithmetischen Aufgabenstellungen und Lernumgebungen verborgen liegen.
