Wie schon mehrfach hervorgehoben, bieten sich die Rechendreiecke zu zahlreichen Entdeckungen, Argumentationen und zum Problemlösen an. Dabei kann und muss eine Unterrichtseinheit oder auch -reihe nicht alles abdecken. Die Rechendreiecke können auch immer wieder über die Schuljahre hinweg genutzt werden, um die Kinder vor andere, neue Herausforderungen zu stellen.
Um Entdeckungen tätigen zu können, sollten sich die Kinder im Aufgabenformat erst sicher bewegen können. Das heißt eine Einführung der Rechendreiecke ist wichtig, damit alle Kinder die Rechenvorschriften verstehen und anwenden können. Eine Unterrichtreihe in der die Rechendreiecke zur Förderung unterschiedlicher prozessbezogener Kompetenzen genutzt werden, könne beispielsweise wie folgt aufgebaut sein:
-
Zahlenformat erkunden
-
Gegeben-Gesucht
-
Operative Veränderungen einer Innenzahl
-
Drei gleiche Innenzahlen
-
Vergleich Innen/Außensumme
Im Folgenden werden alle fünf Einheiten kurz beschrieben.
Hierbei ist es wichtig, dass die Kinder die Aufgabenvorschrift erkennen und anwenden können. Es eignet sich beispielsweise eine Plenumsphase, in der alle Kinder die Rechendreiecke kennenlernen und die Aufgabenvorschrift gemeinsam erörtern. Einfache Aufgabenbeispiele sollten dann von jedem Kind individuell gerechnet werden, um zu überprüfen, dass die Rechenregeln, die hinter diesem Format stecken, angewendet werden können.
Auch diese Phase dient in erster Linie dazu, dass die Kinder sich innerhalb der Rechendreiecke rechnerisch sicher bewegen können. Dazu können an unterschiedlichen Stellen im Rechendreieck Lücken gelassen werden. Die Kinder addieren und subtrahieren hierbei. Eine Differenzierung ist auf unterschiedlichen Ebenen relativ schnell zu realisieren.
Sicherlich lässt sich zum einen auf der Ebene der Zahlen differenzieren. Aber auch die Anzahl und Position der gesuchten Zahlen macht einen Unterschied in der Schwierigkeit aus. Dabei gibt es auch Dreiecke, die dann nicht zwangsläufig nur eine Lösung haben (wenn beispielsweise nur die obere Innenzahl und die rechte und die linke Außenzahl gegeben sind).
In der dritten Phase sollen die Kinder Entdeckungen über die Zusammenhänge in den Rechendreiecken anstellen. Dazu bieten sich sogenannte operative Veränderungen an, da die Kinder „einfache“ Veränderungen beschreiben und begründen können (vergleiche operatives Prinzip).
So kann hierbei beispielsweise immer die obere Innenzahl um 1 erhöht werden und es wird geschaut, was sich verändert. Da sich die obere Innenzahl sowohl auf die linke als auch auf die rechte Außenzahl auswirkt, werden auch diese beiden jeweils um 1 größer.
Erhöht man aber alle drei Innenzahlen gleichzeitig, werden alle Außenzahlen jeweils um 2 größer – jede Erhöhung einer Innenzahl wirkt sich auf zwei Außenzahlen aus, somit wird auch jede Außenzahl um 2 erhöht.
Ebenfalls denkbar ist es, hier bereits den Vergleich der Innen- und der Außensumme zu thematisieren. Wenn alle drei Innenzahlen jeweils um 1 erhöht werden, erhöht sich die Innensumme selbstverständlich um 3. Da dabei jede Außenzahl um 2 erhöht wird, erhöht sich die Summe der drei Außenzahlen um 6.
Egal für welche (eine oder mehrere) operative Veränderungen innerhalb der Rechendreiecke Sie sich entscheiden sollten, vor allem die Beschreibung und Begründung der Veränderungen ist hierbei zentral. Die Kinder können so Vermutungen zu mathematischen Zusammenhängen anstellen und diese überprüfen und begründen.
Es kann ebenfalls zum Entdecken und Verallgemeinern genutzt werden, wenn alle drei Innenzahlen identisch sind. Es bietet sich beispielsweise auch hier ein Vergleich von Innen- und Außensumme zu fokussieren. Dass die Summen immer das Doppelte einer Innenzahl ist, ist auch auf Zahlenebene gut sichtbar.
Gerade hierbei können Verallgemeinerungen sehr gut veranschaulicht werden:
Hierbei können die Kinder beispielsweise die gleichen Säckchen nehmen, da alle drei Innenzahlen identisch sind. Durch die Gegenüberstellung von Innen- und Außensumme, können die Kinder auch schon entdecken, dass die Außensumme das Doppelte der Innensumme ist.
Sicherlich sollen die Kinder das erst mit Zahlen ausrechnen, Vermutungen anstellen und dann erst zur Verallgemeinerung übergehen. Die Zahlenbeispiele sind in der Grundschule (mindestens) genauso wichtig wie die Verallgemeinerung. Gerade dieser Schritt kann aber anschaulich unterstützt werden. Diese Entdeckungen können den Schülerinnen und Schülern aber auch schon für die nächste Aufgabe helfen.
Wenn der Vergleich der Innen- und der Außensumme in den Unterrichtseinheiten bereits aufgetreten ist, kann darauf zurückgegriffen werden, was die Kinder schon entdeckt haben. Die Klärung der Begriffe Innen- und Außensumme ist dabei so oder so unabdingbar. Die Kinder könnten einige Beispiele rechnen, in der sie auch Innen- und Außensumme berechnen.
a) Entdecken: Mit der Aufforderung „Was fällt dir auf?“ werden die meisten Kinder vermutlich feststellen, dass die Außensumme immer das Doppelte der Innennsumme ist.
Aber nur bei der Entdeckung sollte es nicht bleiben – diese Aufgabe bietet sich insbesondere an, um auch die Begründungskompetenzen der Kinder zu fördern.
b) Begründen: Warum ist es das Doppelte? Die Kinder können das sowohl mit ihren vorhandenen (und unterstützten) sprachlichen Mitteln argumentieren. Jede Innenzahl geht in zwei Außenzahlen ein und daher ist jede einzelne Zahl doppelt in der Außensumme.
c) Verallgemeinern: Warum ist es immer das Doppelte? Oder warum ist es immer gerade?
Visuell kann das durch die Säckchendarstellung unterstützt werden:
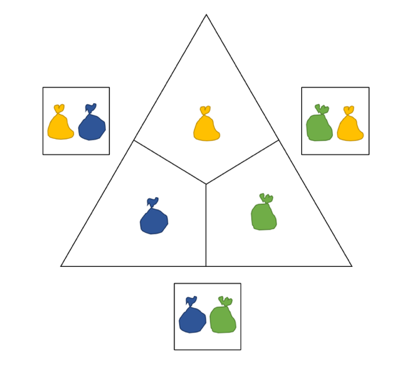
Daraus kann auch abgeleitet werden, dass die Außensumme immer gerade ist. Das Doppelte von etwas ist immer gerade. Je nachdem in welcher Klassenstufe diese Unterrichtsreihe durchgeführt wird, kann das mit den Kindern so auch thematisiert werden.
Je nachdem welchen Schwerpunkt die Unterrichtseinheit thematisiert, brauchen die Kinder verschiedene sprachliche Unterstützung. Dazu gehören sicherlich – wie im Einstieg gesehen – die Bezeichnungen der einzelnen Elemente der Rechendreiecke, aber auch sprachliche Mittel, um die entsprechenden Entdeckungen zu verbalisieren.
Hier finden Sie einen Vorschlag für einen Wortspeicher:
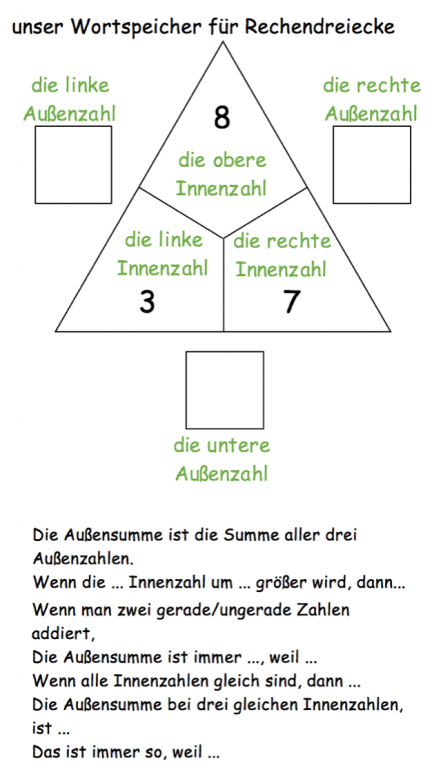
Diese Unterrichtsreihe ist sicherlich nur ein Ausschnitt dessen, was im Bereich der Rechendreiecke möglich und sinnvoll ist.