Bestimmung der Gesamtzahl der Ergebnisse - WIE?
Um die Anzahl von Möglichkeiten zu ermitteln, muss gezählt werden und dies soll möglichst geschickt geschehen. Beim „geschickten Zählen" geht es darum, möglichst einfache Wege zur Anzahlbestimmung zu finden. Häufig wird im Zusammenhang mit der Kombinatorik von "Zählen ohne zu zählen" gesprochen. Schon zu Beginn des ersten Schuljahres wird das geschickte (Ab-) Zählen einzelner Elemente und das Ermitteln der Anzahl der Elemente einer gegebenen Menge thematisiert. Das Rechnen, also das Verwenden von Rechenoperationen wie der Addition, Subtraktion, Multiplikation und Division, ist die Kunst, die vom mühsamen Zählen befreit (vgl. Selter & Spiegel 2004, S. 81). Rechnen ist damit nichts anderes als geschickt zu zählen.
Auf dieser Seite werden zur
Kombinatorik als Prinzip des geschickten Zählens Hintergrundinformationen gegeben:
Kombinatorische Überlegungen - grundschulrelevante Arbeits- und Denkweisen
Wenden wir uns nun der Frage zu, ob Kombinatorik ein Gegenstand des Mathematikunterrichts der Grundschule sein sollte. Die meisten verbinden mit Kombinatorik Formeln, mit deren Hilfe jeweils die Gesamtzahl aller Möglichkeiten berechnet werden kann, und die ganz bestimmt nicht Inhalt des Grundschulunterrichts werden sollen. Im folgenden wird deutlich gemacht, welche Potenziale kombinatorische Aufgabenstellungen und Überlegungen zur Entwicklung inhaltlicher und allgemeiner mathematischer Kompetenzen (hier insbesondere für das Problemlösen) haben. Dazu werden Vorgehensweisen von Kindern bei der Bearbeitung kombinatorischer Problemstellungen an den Anfang gestellt.
Eigenaktivität
Bearbeiten Sie zunächst selbst folgende Aufgabe, bevor wir Vorgehensweisen von Kindern betrachten:
In einem Beutel befinden sich drei verschiedenfarbige Bonbons:
-ein rot-orangenes,
-ein gelbes und
-ein grünes Bonbon
Du ziehst mit einem Griff zwei Bonbons heraus.
Wie groß ist die Chance, dass ein rot-orangenes Bonbon dabei ist?
Was wird hier deutlich und was bedeutet das für die Grundschule?
-
Kindern stehen keine Algorithmen zur Lösung derartiger Aufgaben zur Verfügung.
-
Aufgaben können von den Kindern auf verschiedenen, individuell unterschiedlichen Wegen gelöst werden.
-
Lösungswege sollten öffentlich gemacht, begründet und diskutiert werden.
Derartige Aufgabenstellungen unterstützen somit die Entwicklung prozessbezogener mathematischer Kompetenzen. Es werden Strategien zur Problemlösung genutzt bzw. weiterentwickelt. Kinder verwenden aus ihrer Sicht geeignete Darstellungsformen der Lösungswege und begründen ihr Vorgehen. Individuelle Herangehensweisen sind Grundlage für einen Austausch in der Lerngruppe. Die Reflexion über die individuellen Herangehensweisen öffnet den Blick für unterschiedliche Zugänge zur Problemlösung und unterstützt das Erkennen und das Verständnis mathematischer Strukturen.
Kombinatorische Aufgabenstellungen unterscheiden sich in wesentlichen Punkten von anderen Aufgaben zur Anzahlbestimmung (vgl. Höveler 2014)
-
Ziel ist es die Anzahl aller Möglichkeiten zu ermitteln.
-
Diese müssen erst aus den einzelnen Elementen erstellt werden.
-
Den zu bildenden kombinatorischen Figuren liegen abhängig von der jeweiligen Problemstellung verschiedene Bedingungen zugrunde.
-
Wichtig ist dabei, die Vollständigkeit der Lösungen begründen zu können und Dopplungen bzw. Mehrfachzählungen auszuschließen.
Für die geschickte Bestimmung aller Möglichkeiten gibt es in der Kombinatorik eine Vielzahl verschiedener Lösungswege, die im Folgenden veranschaulicht werden.
Wege und Darstellungsweisen
Peter hat drei Jeans (J1, J2, J3) und fünf T-Shirts (T1, T2, T3, T4, T5)
Auf wie viele unterschiedliche Arten kann er diese miteinander kombinieren?
Auflisten
T1J1, T1J2, T1J3
T2J1, T2J2, T2J3
T3J1, T3J2, T3J3
T4J1, T4J2, T4J3
T5J1, T5J2, T5J3
Tabelle
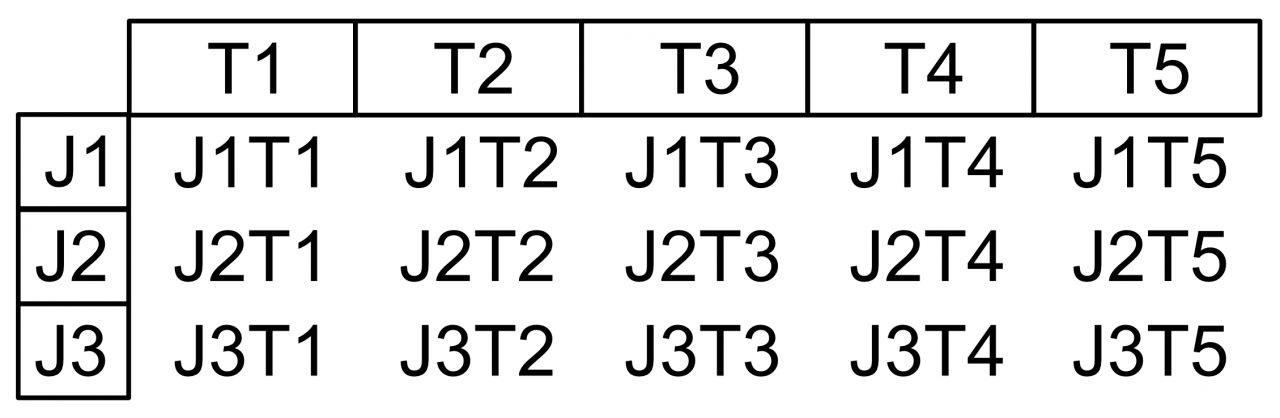
Rechnerische Lösung
Jedes der fünf T-Shirts mit jeder der drei Jeans kombinieren, also 5 ∙ 3 = 15 Möglichkeiten ODER jede der drei Jeans mit jedem der fünf T-Shirts, also 3 ∙ 5 = 15 Möglichkeiten.
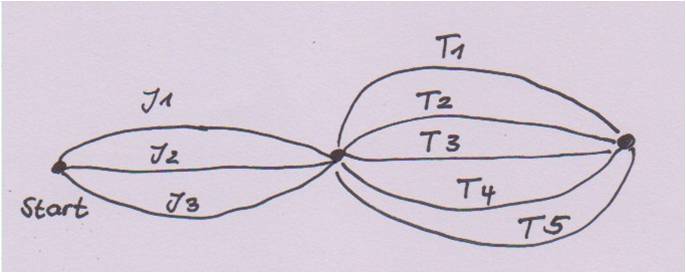 Wegediagramm
Wegediagramm
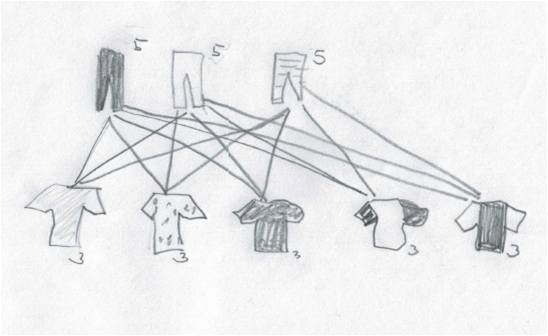 Zeichnerische Lösungen
Zeichnerische Lösungen
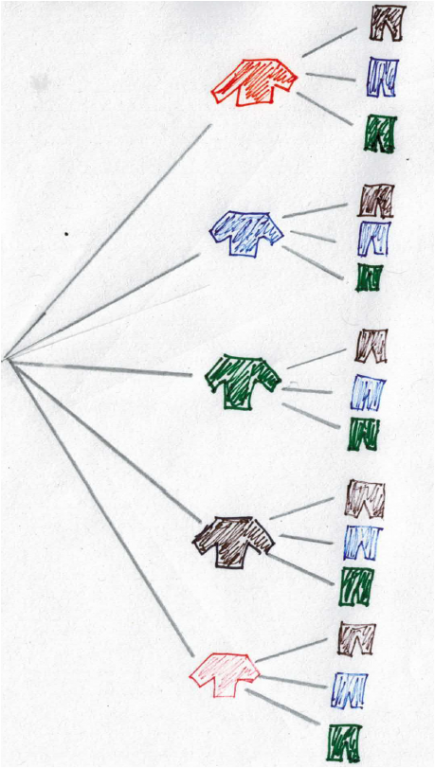 Baumdiagramm
Baumdiagramm
Baumdiagramme sind zwar nicht zur Lösung aller kombinatorischen Probleme geeignet, haben aber weitere Potenzen mit Blick auf die Wahrscheinlichkeitsrechnung.
Ein Baumdiagramm ist geeignet, Überlegungen zu Zufallsversuchen zu veranschaulichen. Die Anzahl günstiger und möglicher Ergebnisse können Kinder ablesen. Sie können Aussagen zur Wahrscheinlichkeit treffen und mithilfe des Baumdiagramms begründen.
Welche kombinatorischen Figuren können unterschieden werden und welche sind für die Grundschule relevat? In der Grundschule kommt es auf eine inhaltliche Analyse der kombinatorischen Aufgabenstellungen an. Das Finden von Mustern und Strukturen unterstützt das Finden und Nutzen von Darstellungen und Rechenwegen. Die Reflexion des Vorgehens und das Hervorheben erkannter Muster und Strukturen unterstützen das Lernen von tragfähigen Strategien und das inhaltliche Verständnis der jeweiligen kombinatorischen Figur. Auf diese Art und Weise werden Verallgemeinerungen in der Sekundarstufe und eine folgende Beschreibungen in Form von Formeln möglich und inhaltlich verstanden.
Bei der Ermittlung aller Möglichkeiten geht es um ein „geschicktes“ Bestimmen von Anzahlen. Das allgemeine Zählprinzip nennt man auch Produktregel oder Multiplikationsregel. Dabei können die Plätze in beliebiger Reihenfolge besetzt werden. Bereits hier auftretende Unterschiede werden in den folgenden „Figuren“ aufgegriffen.
Bei der Klassifizierung der kombinatorischen Figuren werden immer wieder folgende Fragen gestellt:
-
Werden alle gegebenen Elemente benötigt oder nur eine Auswahl?
-
Werden die Elemente nur einmal oder dürfen sie mehrfach verwendet werden?
-
Ist die Reihenfolge unerheblich oder muss die Reihenfolge beachtet werden?
Auf diese Art und Weise werden nachfolgend mögliche kombinatorische Figuren durch Aufgabenbeispiele illustriert, die man in Grundschullehrwerken finden kann.
Anordnungsprobleme - die Reihenfolge ist wichtig
-
Betrachten wir zunächst Beispiele bei denen alle vorhandenen Elemente in jedem Fall benötigt werden.
Zunächst betrachten wir ein Aufgabe bei der jedes Element nur einmal verwendet werden darf.
Wie viele dreistellige Zahlen können aus den Ziffern 2, 4, 6 gebildet werden? Jede Ziffer darf dabei nur einmal verwendet werden.

Die Reihenfolge der Ziffern ist wichtig (Stellenwert).
Auflisten aller Lösungen
246, 426, 624, 264, 462, 642
Baumdiagramm
rechnerisch 3 ∙ 2 ∙ 1 = 6 Zahlen
Anordnungen von Flächen und Körpern sind analoge Problemstellungen, die auf diese Art und Weise gelöst werden können. Derartige Anordnungen werden als Permutation von n Elementen ohne Wiederholung bezeichnet.
Übersicht, in der die Infomationen zur kombiantorischen Figur, einschließlich der Berechnungsvorschrift zusammengestellt sind:
Wie verändert sich die Lösung, wenn ein Element mehrfach verwendet wird?
Wie viele dreistellige Zahlen können aus den Ziffern 2 und 6 gebildet werden, wenn die Ziffer 6 zweimal auftreten soll.
Auch hier ist, wie im Vorgängerbeispiel, die Reihenfolge der Ziffern von Bedeutung (Stellenwert).
Auflisten aller Lösungen
266, 626, 662
Baumdiagramm
rechnerisch
Wären es drei verschiedene Ziffern, gäbe es (wie im vorhergehenden Beispiel) sechs Möglichkeiten. Da die 6 doppelt vorkommt, ist durch zwei zu dividieren, denn die beiden Sechsen können nicht unterschieden werden.
Analoge Problemstellungen wären weitere Ziffern-Zahlbildungen wie Zahlen aus 2x Ziffer 1 und 3x Ziffer 8.
Diese Anordnungen sind Permutation von n Elementen mit Wiederholung.
-
Betrachten wir als nächstes Beispiele für Anordnungen bei denen nicht alle vorhandenen Elemente verwendet werden.
An einem 40m-Lauf nehmen acht Läufer teil.
Wie viele Möglichkeiten der Belegung der ersten drei Plätze gibt es?
Offensichtlich werden nicht alle „Elemente“ benötigt, denn es können nur drei der acht Läufer die ersten drei Plätze belegen. Die Reihenfolge ist wichtig, denn Erster oder Dritter zu sein ist ein Unterschied. Wiederholungen sind nicht möglich, denn jeder Läufer kann nur einmal durchs Ziel laufen.
Überlegungen: Für Platz 1 gibt es acht, für Platz 2 dann noch sieben und Platz 3 noch sechs Moglichkeiten des Einlaufs.
Überlegungen: Für Platz 1 gibt es acht, für Platz 2 dann noch sieben und Platz 3 noch sechs Möglichkeiten des Einlaufs.
(rechnerisch) Damit insgesamt:
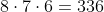 Möglichkeiten
Möglichkeiten
Eine analoge Problemstellung wäre: Wie viele dreistellige Zahlen lassen sich aus 5 verschiedenen Ziffern bilden? Jede Ziffer darf nur einmal in jeder Zahl auftreten.
Derartige Anordnung werden als Variation ohne Wiederholung bezeichnet.
Im folgenden Beispiel wird eine Variation mit Wiederholung betrachtet.
Es gibt Steckwürfel in vier unterschiedlichen Farben (rot, blau, gelb, grün). Wie viele unterschiedliche Dreiertürme können gebaut werden?
 Bildunterschrift
Bildunterschrift
Es werden nur drei Steine genommen.
Wiederholungen sind möglich, denn die vier Farben können mehrfach auftreten. So gibt es u. a. auch einen Dreierturm aus drei roten Bausteinen.

Die Reihenfolge ist wichtig, denn beispielsweise ist ein Turm
rot – blau – gelb anders als gelb – rot – blau.
Überlegungen
Stein 1 - vier mögliche Farben
Stein 2 - vier mögliche Farben
Stein 3 - vier mögliche Farben
(rechnerisch) Damit insgesamt:
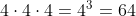 Türme
Türme
Analoge Problemstellungen wären die Bildung von Palindromen (ANNA-/OTTO-Zahlen) bzw. die Bildung von dreistelligen Zahlen aus drei von 0 verschiedenen Ziffern, wobei jede Ziffer mehrfach vorkommen kann.
Allgemein gilt: Für eine
Variation mit Wiederholung gibt es
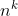
Möglichkeiten.
Bisher haben wir nur kombinatorische Figuren betrachtet bei denen die
Reihenfolge der Elemente beachtet werden musste. Zum Abschluss werden noch Beispiele betrachtet, bei denen die Reihenfolge bei der Anzahlermittlung keine Rolle spielt.
Auswahlprobleme - die Reihenfolge ist nicht wichtig
Es sind fünf verschiedene Punkte gegeben, von denen nicht drei auf einer Geraden liegen. Wie viele Geraden (Verbindungsstrecken) können gezeichnet werden?
Es sind immer zwei der fünf Punkte zu verbinden. Die Reihenfolge ist unwichtig, denn die Geraden AB und BA sind identisch. Wiederholung ist nicht möglich, denn wählt man zweimal A kann keine Gerade gezeichnet werden.
Zeichnerische Lösung
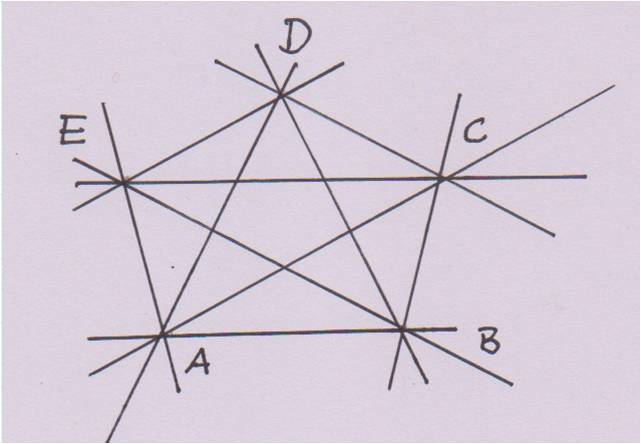 10 Verbindungslinien
10 Verbindungslinien
Auflistung
AB BC CD DE
AC BD CD
AD BE
AE
rechnerisch:
Jeder der fünf Punkte kann mit vier anderen verbunden werden. Wenn diese Linien zu unterscheiden wären, gäbe es 5 ∙ 4 = 20 Möglichkeiten. Da aber AB und BA nicht zu unterscheiden sind, werden Möglichkeiten doppelt gezählt. Es muss also durch zwei dividiert werden.
Analoge Problemstellungen wären: Hände-schütteln, Gläser-anstoßen, Lotto 6 aus 49
Das sind Beispiele für eine Kombination ohne Wiederholung (k Elemente aus n auswählen, Reihenfolge ist nicht wichtig).
Nun betrachten wir noch eine Kombination mit Wiederholung.
Wie viele Steine hat ein Dominospiel, bei dem die Punktbilder von 0 bis 6 auftreten?
Es können je zwei Punktbilder für einen Stein ausgewählt werden. Wiederholungen sind möglich, denn es gibt Steine, auf denen ein Punktbild zweimal auftritt. Die Reihenfolge ist unerheblich, da Steine beliebig gedreht werden können.
Auflistung
0|0 1|1 2|2 3|3 4|4 5|5 6|6
0|1 1|2 2|3 3|4 4|5 5|6
0|2 1|3 2|4 3|5 4|6
0|3 1|4 2|5 3|6
0|4 1|5 2|6
0|5 1|6
0|6
rechnerisch: Die Möglichkeiten sind zu addieren. Das Fundamentalprinzip (Multiplikation) ist hier nicht anwendbar. Ein Baumdiagramm kann nicht erstellt werden.
Eine analoge Aufgabenstellung wäre: Aus einem Topf 3 Kugeln ziehen (mit Zurücklegen).
Auch unter diesem Link Kombination mit Wiederholungn finden sie, wie bei allen anderen Beispielen, die wichtigsten Infomationen zur kombiantorischen Figur, einschließlich der Berechnungsvorschrift zur Ermittlung alle Möglichkeiten.
Unter KIRA: Daten, Häufigkeiten und Wahrscheinlichkeiten – Kombinatorik können Sie sich zum Thema Geschicktes Zählen weiter informieren.