Kinder beim Weiterlernen unterstützen
Eine Heranführung an schulische Leistungsanforderungen kann durch eine stärkere Einbindung der Kinder in die Leistungsbewertung geschehen (vgl. hierzu auch die Primakom-Seite Leistungen rückmelden). Werden die Kinder in die Leistungsbewertung einbezogen, werden sie in die Verantwortlichkeit für ihren Lernprozess eingebunden. Steht Leistungsbewertung im Zweck der Verbesserung des Lernens statt der Klassifizierung von Leistungen, kann die Lernfreude der Kinder erhalten und deren Leistungsfähigkeit entwickelt werden. „Unterstützen statt überprüfen heißt die vorrangige Aufgabe“ (Sundermann & Selter 2006, S. 8).
Darüber hinaus geht es darum, von den Kindern nicht nur Leistungen zu fordern, sondern ihnen Möglichkeiten zu bieten Leistungen zu erbringen. Doch was bedeutet das konkret für den Unterricht?
Um die Frage "Welche Arten von Leistungsfeststellungen können im Unterricht ergänzend eingesetzt werden, um Kinder beim Weiterlernen zu unterstützen?" zu beantworten, werden im Folgenden exemplarisch zwei alternative Verfahren der Leistungsfeststellung vorgestellt, die ergänzend eingesetzt werden können, um Kinder beim Weiterlernen zu unterstützen:
Es gibt viele Möglichkeiten die Leistungsfeststellung in den alltäglichen Unterrichtsalltag zu integrieren. Neben Klassenarbeiten und Bewertung der mündlichen Mitarbeit können Standortbestimmungen, Informative Aufgaben, sogenannte Zertifikate oder Wochenpläne eingesetzt werden, die Leistungen der Kinder zeitlich flexibel festzustellen. Standortbestimmungen können beispielsweise dazu dienen, die Vorkenntnisse der Schülerinnen und Schüler zu einem Thema zu erheben. Mehr Informationen erhalten sie auf der Primakom-Seite Standortbestimmungen.
Leistungen feststellen mit dem Mathebriefkasten
Der Mathebriefkasten kann eingesetzt werden um, in Form von kleineren offen angelegten Aufgaben etwas über den Kenntnis- und Fähigkeitsstand der Kinder zu erfahren. Wie im Hintergrund bereits verdeutlicht wurde, ermöglicht die Arbeit mit informativen Aufgaben einen regelmäßigen und unkomplizierten Einblick in individuelle Lernstände der Kinder. Im Folgenden soll nun genau beschrieben werden, wie Sie den Mathebriefkasten in ihre Unterrichtsarbeit integrieren können.
Wie Sie im Hintergrund bereits erfahren haben, ist der Mathebriefkasten als eine Organisationsform zu betrachten. Grundsätzlich ist es natürlich egal, wie der Mathebriefkasten aussieht, ein beklebter Schuhkarton mit Schlitz ist nur eine mögliche Variante.
Natürlich gelingt die Einführung des Mathebriefkastens nicht von heute auf morgen. „Es bedarf einer Unterrichtskultur, in der die Kinder sich und ihre Vorgehensweisen mitteilen möchten, keine Angst vor Fehlern haben und Fehler als Lernmöglichkeit verstehen“ (Höveler & Akinwunmi 2017, S. 146).
Für die Arbeit mit dem Mathebriefkasten ist es hilfreich einige Punkte zu beachten, die im Folgenden kurz erläutert werden sollen.
Ritualisierung
Für eine ritualisierte Umsetzung des Konzepts Mathebriefkasten ist es hilfreich, regelmäßige Zeitpunkte festzulegen, z.B. 14tägig, oder einmal im Monat. Am Ende oder zu Beginn einer dafür festgelegten Unterrichtsstunde kann den Kindern eine Aufgabe gestellt werden, die sie erledigen können. Sobald sie fertig ist, werfen sie ihre individuellen Aufgabenbearbeitungen und Erklärungen an die Lehrerin oder den Lehrer in einen Briefkasten oder geben die Bearbeitungen an den Lehrer ab.
Die Aufgaben sollten so gestellt sein, dass sie nicht länger als fünf bis zehn Minuten in Anspruch nehmen, aber einen guten Einblick in das Denken der Kinder geben (Sundermann & Selter 2011, S. 171). Dazu eignen sich insbesondere informative Aufgaben, wie bereits ausführlich im Hintergrund dargestellt.
Zieltransparenz
Das Interesse an den Denkwegen der Kinder sollte im Vordergrund stehen und auch den Kindern transparent gemacht werden. Diese Transparenz über Zeitpunkt und Zielsetzung der Mathebriefe kann den Prüfungsdruck vermindern und Diagnose kann als natürliches Element des Unterrichts erfahren werden. Ggf. kann ergänzend hinzugefügt werden:
„Erkläre so, dass ich verstehen kann, wie du gedacht hast!", damit den Kindern deutlich wird, dass es nicht allein um Lösungen, sondern um eine „Hilfestellung" für die Lehrerin/ den Lehrer zur weiteren Unterrichtsplanung geht.
Wiederholung
Mit der kontinuierlichen Diagnose können die Lernentwicklungen über einen längeren Zeitraum erfasst werden, indem die Lehrkraft denselben Mathebrief mehrfach, mit zeitlichem Abstand schreiben lässt.
 Eigenaktivität
Eigenaktivität
In einer Klasse wurden die Kinder jeweils im Abstand mehrerer Wochen gebeten, die Aufgabe 8・9 zu lösen. Schauen Sie sich die Lösungen von Achim an. Welche Entwicklung können Sie feststellen?
 entnommen aus Selter 2013
entnommen aus Selter 2013
Stellt man den Kindern dieselbe Aufgabe mehrfach, lässt sich über ein Schulhalbjahr hinweg die Entwicklung der Kompetenzen beobachten und dokumentieren. Ergänzend ist es denkbar, sich die Kinder über ihren Lernfortschritt selbst äußern zu lassen. Somit wird zum einen der eigene Lernfortschritt transparent gemacht, weiterhin kann durch kontinuierliche Reflexion eigener Bearbeitungen die Selbsteinschätzungsfähigkeit verbessert werden.
Beispielsweise könnte den Kindern ihre eigenen Mathebriefe vorgelegt werden mit dem Arbeitsauftrag den eigenen Lernfortschritt zu beschreiben.
Vergleiche deine Lösungen! Welche Unterschiede siehst du?

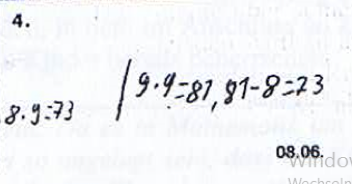
Was hast du dazugelernt?

Dokumentation
Wichtig ist, dass die Schüler das Datum und natürlich auch ihren Namen auf dem Aufgabenblatt notieren, damit eine eindeutige Zuordnung möglich ist. Mathebriefe können so geordnet für jedes Kind gesammelt werden, um deren Lernentwicklung zu dokumentieren.
Das Datum wird insbesondere dann wichtig, sobald eine Entwicklung über Lösungsstrategien ein und derselben Aufgabe dokumentiert werden soll (Abbildung 13).
Für einen systematischen Überblick über die individuellen Lernstände hat sich das Ausfüllen einer Übersichtstabelle (Abbildung 14) als nützlich erwiesen. So erhält man einen guten Überblick über den Lernstand der Klasse, zu den jeweiligen Zeitpunkten (Spalten) und die Entwicklung einzelner Kinder über die Zeit hinweg (Zeilen).
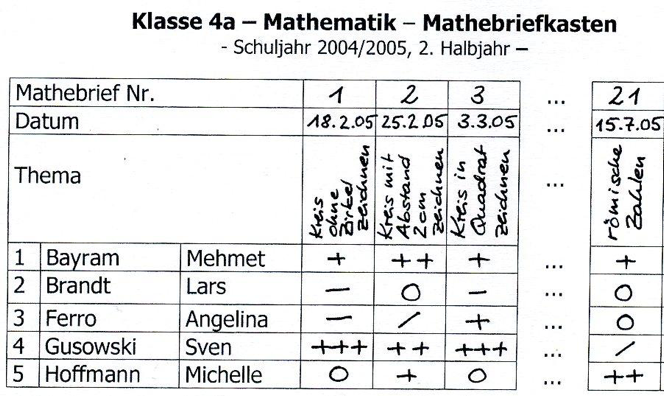 Auswertungsbogen
Auswertungsbogen
Werden in kurzer Zeit und bezogen auf ein bestimmtes Thema vergleichsweise viele solcher Aufgaben gestellt, bietet sich auch eine themenbezogene Klassenliste an. Auswertungsbogen zum Download finden Sie unter PIKAS: Unterrichtsmodul: Leistung - Lernstände wahrnehmen .
Rückmeldung
Grundsätzlich bieten die Mathebriefe, neben dem Informationsgehalt für die Lehrkraft, die Möglichkeit der Kommunikation mit einzelnen Schülern.
Dabei muss die Rückmeldung nicht immer schriftlich oder an alle Kinder der Klasse erfolgen. Denkbar sind kurze mündliche oder schriftl. Rückmeldung an einzelne Kinder, Rückmeldungen an einzelne Kinder innerhalb einer Kindersprechstunde (PIKAS: Selbststudiumsmodul: Beurteilen und Rückmelden - Videos - Kindersprechstunde) oder an Kindergruppen. Ebenso sind pauschale Rückmeldungen an die gesamte Klasse möglich. Mehr dazu unter PIKAS: Fortbildungsmodul: Beurteilen und Rückmelden – Leistungen lernförderlich rückmelden.
 Rückmeldung per Haftnotiz (aus Modul 9.3 pikas.dzlm.de/172)
Rückmeldung per Haftnotiz (aus Modul 9.3 pikas.dzlm.de/172)
Reflexionsanregung/ Integration im Unterricht
Weiterhin eigen sich Mathebriefkasten-Aufgaben für anschließende Unterrichtsgespräche. Verschiedene Schülerbearbeitungen können miteinander verglichen werden, um die wesentlichen Elemente einer Uhr zu erarbeiten.
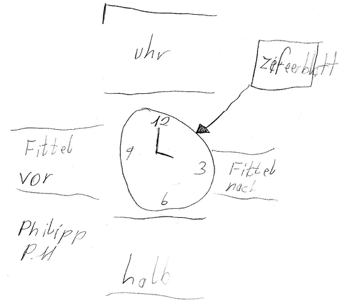
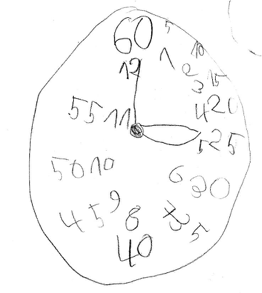

Wichtig ist dabei, dass keine Bearbeitungen als falsch oder schlecht beurteilt werden, sondern dass alle Leistungen entsprechend gewürdigt werden. Je nach Thema bieten sich unterschiedliche Impulsfragen an.
Für die Weiterarbeit mit der Uhr bieten sich beispielsweise folgende Impulsfragen an:
-
Wozu braucht man eine Uhr?
-
Was gehört alles auf eine Uhr?
-
Was bedeuten die Striche?
-
....
Beobachtungsmöglichkeiten auf Seiten der Lehrkraft sind dabei dieselben, wie bereits im Einstieg durch strukturgebende Fragen formuliert.
Wie differenziert kennen die Kinder Merkmale normierter Messgeräte?
Welche Vorstellungen haben sie über den Aufbau einer Uhr entwickelt? (z.B. Wissen um die Skalierung und die Relationen zueinander. Wissen um die Funktionsweise und die Einheiten.)
Gleiche oder ähnliche Fragen gelten für alle normierten Messgeräte (z.B. Lineal). Bei anderen Unterrichtsinhalten konnten die Fragen anhand der gewünschten Kompetenzen gewählt werden. Vergleiche von Aufgabenmerkmalen (vgl. Schriftliche Subtraktion im Hintergrund) können ebenso mit Kindern angestellt werden.
Welche Gemeinsamkeiten und Unterschiede bestehen zwischen den Aufgaben? Worauf muss man hier besonders achten? Usw.
Zertifikate
Weitere Formen der Feststellung von aktuellen Leistungsständen können sogenannte Zertifikate, Pässe oder Diplome sein.
Ein Zertifikat ist ein Laufzettel, auf dem ein Thema oder Inhaltsbereich in einzelne Teilleistungen, Teilübungen gegliedert ist. Es bietet den Kindern einen inhaltlichen Überblick über die Leistungsanforderungen und unterstützt zudem die selbstständige Arbeit im Hinblick auf ein zu erreichendes Ziel.
Punktueller Einsatz
Besonders im offenen oder inklusiven Unterricht, in dem nicht alle Kinder im gleichen Tempo arbeitet, bietet sich die Arbeit mit Zertifikaten an.
Zertifikate, Pässe oder Diplome können den Unterricht nicht ersetzen, sondern punktuell und dosiert eingesetzt sinnvoll ergänzen (vgl. Sundermann & Selter 2006, S. 37). Diese Formen der Leistungsfeststellung eignen sich insbesondere das selbstständige Üben/ Einüben von Fertigkeiten oder Kenntnissen, wie beispielsweise das kleine 1+1). Aber auch prozessbezogene Kompetenzen oder eine längerfristige Stationenarbeit, kann mithilfe solcher Formen der Leistungsfeststellung überprüft werden (vgl. hierzu auch Sundermann & Selter 2006, S. 39f.).
Die Arbeit mit Zertifikaten erfordert eine gute und strukturierte Vorbereitung von Seiten der Lehrerin:
-
Gliederung eines Themas in mehrere Teilaspekte, die selbstständig von den Schülern zu bearbeiten sind
-
ergänzende Übungsmöglichkeiten zu den einzelnen Teilaspekten, die ebenso eine Selbstkontrolle enthalten
Hat ein Kind alle Teilaufgaben erledigt, erfolgt eine Prüfung über die geübten Aufgabenteile.
Die Arbeit mit Zertifikaten wird an dieser Stelle beispielhaft am Blitzrechenpass (aus: Sundermann & Selter 2006, S. 39) vorgestellt (vgl. Abb. 1).
Die Auflistung der Teilaspekte zum Blitzrechnen ist eng gekoppelt an das Material, das zur Übung herangezogen werden kann. So gibt es zu jeder Teilleistung spezielle Karten in der Blitzrechenkartei, mit denen die jeweiligen Fähigkeiten trainiert werden können (vgl. Blitzrechenkartei, Müller & Wittmann 2013).

Selbstverantwortung
Wesentlich bei der Arbeit mit Zertifikaten ist die selbstständige (Übungs-)Tätigkeit der Kinder. Je nach Inhalt allein oder in Partnerarbeit üben die Kinder die Teilleistungen z.B. das Mini-Einmaleins der Blitzrechenkartei. Durch gemeinsames Üben und Abfragen führen kontinuierlich Partnerkontrollen durch und üben gleichzeitig die Prüfungssituation mit der Lehrerin. Dies ermöglicht es den Kindern ihre Leistungen im geschützten Rahmen zu überprüfen und lernen zunehmend sich selbst und ihre Leistungsfähigkeit besser einzuschätzen.
Die Kinder entscheiden eigenständig, wann sie eine Teilprüfung oder auch die Abschlussprüfung absolvieren wollen. Damit erfüllt diese Art der Leistungskontrolle das Kriterium der Differenzierung. Die Kinder wählen individuell Zeitpunkt und Dauer der einzelnen Übungseinheiten, dies reduziert den Leistungsdruck. Entscheidet sich ein Kind die Prüfung abzulegen, meldet es sich bei der Lehrkraft. Die Lehrkraft sollte dabei darauf achten, dass einzelne Kinder die Prüfung/ Abfrage der Teilleistungen nicht zu lange hinauszögern. Die Lehrerin bewertet die Leistungen in diesen Prüfungen auf einer dreistufigen Skala von – bis + (vgl. Abb. 1).
Transparenz
Besonders zu Beginn der Arbeit mit dieser Form der Leistungsüberprüfung, kommt es vor, dass die Kinder die Prüfung nicht beim ersten Mal erfolgreich abschließen und diese wiederholen müssen. Dies sollte den Kindern vorher transparent gemacht werden, dabei sollte ebenfalls klar werden, dass die Kinder trotzdem mit einer gewissen Ernsthaftigkeit an die Prüfung herangehen. Die Kinder sollen lernen sich und ihre Leistungsfähigkeit selbst und (zunehmend) realistischer einschätzen können. Daran zeigt sich, dass die Selbsteinschätzung ebenfalls Lerninhalt ist. Voraussetzung für die Arbeit mit Zertifikaten ist, dass die Kinder bereits Erfahrungen zu Selbsteinschätzungen und Feedback gesammelt haben. Dies kann zuvor mit Aufgaben, wie „Teste dich selbst“ oder „Teste deinen Partner“ geübt werden.
Übersichtlichkeit
Im Blitzrechenpass werden dazu neben der Dokumentation und Bestätigung einer Abschlussprüfung auch die beinhalteten Teilaspekte aufgelistet (vgl. Abb. 1), die in Form von Einzelabfragen überprüft werden. Vorteil der Arbeit mit Zertifikaten ist die gleichzeitige Dokumentation des Zeitpunktes der erbrachten Leistungen. Zertifikate bieten Sie eine gute Möglichkeit der Dokumentation von Leistungen sowohl für die Schülerinnen und Schüler, als auch für die Lehrkraft.
Der Blitzrechenpass stellt nur eine Möglichkeit dar, die Anforderungen an die Schülerinnen und Schüler durch Zertifikate transparent zu machen und die entsprechenden Leistungen zu dokumentieren. Das Prinzip lässt leicht auf andere Inhalte übertragen. Ebenso sind Abwandlungen bezogen auf die Anforderungen eines jeden anderen Themas möglich. Weitere Beispiele hierzu, wie das Matheforscher-Diplom oder die Würfelbaumeister-Urkunde, finden sich in Sundermann & Selter (2006, S. 40ff.) und unter PIKAS: Unterrichtsmodul: Raum und Form – Bauen mit SOMA-Würfel-Teilen.