Konzepte eines sprachsensiblen Mathematikunterrichts
Sprachförderung wird in allen Fächern gefordert und es gibt bereits Konzepte und Ansätze zur Förderung aus dem Deutschbereich für den Zweit- und Fremdsprachenerwerb.
Doch wie sieht dies im Mathematikunterricht aus?
Zur Klärung wird im Folgenden diesen Fragestellungen nachgegangen:
Warum ist ein sprachsensibler Mathematikunterricht wichtig?
In der aktuellen Unterrichtsforschung herrscht Konsens darüber, dass sprachliche Kompetenzen auf Seiten der Kinder von großer Bedeutung für den Lernerfolg in allen Fächern sind:
-
Sprachlich schwache Kinder gehören in der Regel auch zu den mathematisch schwachen Kindern, d. h. gewisse Sprachkompetenzen scheinen grundlegend zur Ausbildung mathematischer Kompetenzen zu sein (vgl. Heinze, Herwartz-Emden & Reiss 2007).
-
Es gibt einen positiven Zusammenhang zwischen fachintegrierter Sprachförderung und der Entwicklung sprachlicher und fachlicher Kompetenzen der Kinder (vgl. Rösch & Stanat 2011).
-
Anspruchsvolle Fachleistungen können nur zum Ausdruck erbracht werden, wenn die Kinder über die entsprechenden bildungssprachlichen Kompetenzen verfügen (vgl. Cummins 2000).
-
Das mündliche wie auch schriftliche Versprachlichen kann dazu dienen, die Gedanken zu strukturieren sowie Fehler im Lösungsprozess zu identifizieren (vgl. Götze 2010).
Ein Zugang zur Bildungs- und Fachsprache gilt nachweislich als Schlüsselkompetenz, um höhere Lernziele und Schulerfolge zu erreichen. Allen Kindern sollte daher die Möglichkeit gegeben werden, diese Bildungs- und Fachsprache zu erlernen. So werden die Kinder während der Grundschulzeit im Mathematikunterricht mit etwa 500 fachspezifischen Begrifflichkeiten und Formulierungen konfrontiert (vgl. Krauthausen 2007).
Dabei geht es nicht allein um Fachbegriffe wie "Ergebnis", "Addition", "Subtraktion", "Multiplikation", "Division" usw. Auch mit ganz besonderen mathematischen Sprech- und Ausdrucksweisen umzugehen, müssen die Kinder lernen. Satzgefüge wie z. B. "wird immer um x größer/kleiner" oder "Wenn die Summanden um je 1 erhöht werden, dann ..." werden typischerweise nur im Kontext Mathematik verwendet.
Das Erlernen dieser spezifischen Ausdrucksweisen ist zentral, um dem Mathematikunterricht besser folgen zu können und damit Mathematik überhaupt zu verstehen. Zeitgleich wird durch die Förderung der mathematikspezifischen Sprech- und Ausdrucksweisen eine geteilte Sprachbasis geschaffen, die die Kommunikation über Mathematik erleichtert (vgl. Götze 2015).
Unterschied von Alltags-, Bildungs- und FachspracheIn diesem Pdf-Dokument können Sie mehr über den Unterschied von Alltags-, Bildungs- und Fachsprache erfahren (vgl. Götze 2015).
Eigenaktivität
Überlegen Sie, welche mathematikspezifischen Formulierungen Sie benötigen, um das Muster in dem folgenden Entdecker-Päckchen zu beschreiben:
1 + 8 = 9
3 + 8 = 11
5 + 8 = 13
7 + 8 = 15
9 + 8 = 17
Die große Frage, die sich hier nun stellt ist, wie (ausgehend von den alltagssprachlichen Kompetenzen der Kinder) die Sprache des Mathematikunterrichts im täglichen Unterrichtsgeschehen mitgefördert werden kann.
Wie kann die Sprache im täglichen Unterrichtsgeschehen gefördert werden?
Zur Förderung eines sprachsensiblen Mathematikunterrichts kann ebenfalls der aus dem Deutschbereich bekannte sogenannte Scaffolding Ansatz dienen.
Der Scaffolding Ansatz
Der englischsprachige Begriff "Scaffolding" (vgl. Gibbons 2006) bedeutet übersetzt "Gerüstbau". Diese Metapher verdeutlicht den Grundgedanken eines sprachsensiblen Fachunterrichts:
-
Ausgehend von den individuellen sprachlichen Kompetenzen der Kinder, werden den Kindern sprachliche "Gerüste" angeboten, an denen sie sich orientieren können; an denen sie sich anlehnen können.
-
Diese sprachlichen Gerüste werden im Lernprozess zunehmend individuell wieder abgebaut, sodass die Kinder nun in der Lage sind, ohne diese Stütze zu arbeiten.
In der Regel werden zwei verschiedene Ansatzpunkte des Scaffolding unterschieden: Das Makro- und das Mikro-Scaffolding.
Makro-Scaffolding
Unter Makro-Scaffolding werden alle von der Lehrperson vorab geplanten Unterstützungs- und Förderangebote verstanden. Hierzu zählen z. B. Wortspeicher bzw. Wörterlisten, Satzanfänge, sprachliche Angebote auf Arbeitsblättern, Lückentexte...
Wie Sie diese Planungselemente auf der Makroebene im Mathematikunterricht implementieren können, erfahren Sie im Unterrichtsteil.
Mikro-Scaffolding
Das Mikro-Scaffolding stellt einen sehr zentralen Unterstützungsansatz dar: Nämlich den auf der spontanen Interaktionsebene. Demnach versteht man unter Mikro-Scaffolding all die Unterstützungsmaßnahmen, die ungeplant und in der spontanen Interaktion zwischen den Kindern oder zwischen den Kindern und Ihnen entstehen.
Dabei ist zentral, dass Sie Ihre Kinder immer wieder zur Benutzung der fachspezifischen Sprache direkt auffordern. Zeitgleich sollten Sie aber auch ein sprachliches Vorbild für die Kinder und somit in Ihren sprachlichen Formulierungen nicht sprunghaft, alltagssprachlich oder ungenau sein. Nur dann wird die Förderung Effekte zeigen.
Eine sprachsensible Gesprächsführung kann durch folgende Gesprächstechniken geschaffen werden (vgl. Gibbons 2006):
-
Sprechen über das Sprechen (z. B. Wie musst du als Mathematiker sprechen?)
-
Ermutigung zu längeren und/oder fachlichen Äußerungen
-
indirekte Bereitstellung von Fachsprache durch Nachfragen
-
Umformulierungen durch die Lehrkraft
-
direkte Unterstützung durch Fachbegriffe/Fachformulierungen
Im Folgenden sehen Sie eine Szene aus einem sprachsensiblen Partnerinterview mit Viertklässlern (vgl. Arens 2015).
In den Interviewsitzungen zuvor wurde gemeinsam ein Wortspeicher erarbeitet. Detaillierte Hinweise zur Erarbeitung von und zum Umgang mit Wortspeichern finden Sie im Unterrichtsteil.
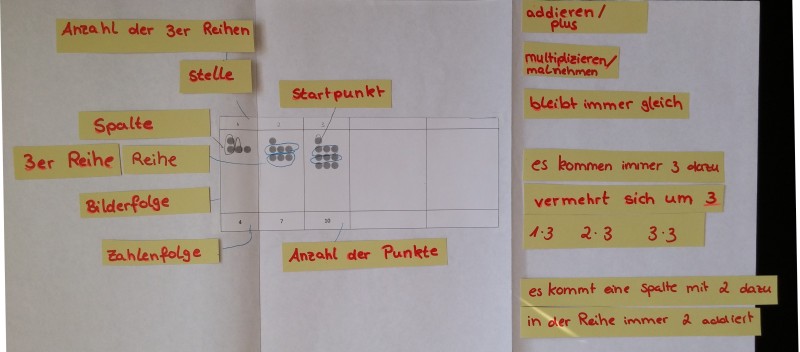
Die Kinder haben die Aufgabe bekommen, die mit den Worten ,,Beginne mit 5 und addiere immer 2.'' beschriebene Zahlenfolge mit Plättchen nachzulegen:
Die beiden Jungen Simon und Alex haben folgende Zahlenfolge gelegt.
Eigenaktivität
Analysieren Sie den folgenden Interviewabschnitt im Hinblick auf diese Frage:
Welche der oben beschriebenen Gesprächstechniken setzt die Interviewerin ein, um die Kinder aufzufordern, ihre Formulierungen zu präzisieren, obwohl sie an manchen Stellen durchaus schon mathematisch korrekte Begrifflichkeiten aus dem Wortspeicher in ihren Formulierungen benutzen?
1. Alex: Hier habe ich eine Spalte gemacht mit fünf Plättchen ... und hier unten habe ich immer zwei gemacht. Dreimal die Zwei.
2. Interviewerin:Mhm, was kann man denn dazu sagen?
3. Alex: Mmh, boah.
4. Interviewerin: Kann man da vielleicht einen Satz hiervon (zeigt auf den Wortspeicher) benutzen?
5. Alex: Mmh ... äh ... äh, warte mal (schaut in den Wortspeicher), so Bilderfolge.
6. Interviewerin: Mhm (zustimmend). Wo ist denn da die Bilderfolge? Kannst du das einmal zeigen, bei dir, bei dir?
7. Alex: Ja, weil ich hab ja das erste gemacht (zeigt auf das Startbild), und dann immer mehr, und dann das zweite mit zweimal mit die Zwei und hier auch die Fünf (zeigt auf die fünf Plättchen in der Spalte im zweiten Bild) und hier (zeigt auf das dritte Bild) hab ich die dreimal die Zwei.
8. Interviewerin: Okay, super.
9. Alex: Und hier (zeigt auf die Spalte), hab ich auch die Fünf.
10. Interviewerin: Simon, kannst du hier vielleicht einen Satz dazu benutzen, was da immer passiert ist? Was passiert von Bild zu Bild?
11. Simon: Mmh (schaut in den Wortspeicher und auf die Bilderfolge). Es werden immer zwei dazu addiert.
12. Interviewerin:Mhm (zustimmend), könnte ihr vielleicht auch mal mit dem Satz etwas sagen (zeigt auf den Wortspeicher)? Was steht da?
13. Alex: Bleibt immer gleich.
14. Interviewerin:Gibt es etwas, das immer gleich bleibt?
15. Simon: Ähm, diese fünf Punkte (zeigt auf die fünf Plättchen in der Spalte).
16. Interviewerin:Okay, aber mach daraus nochmal einen ganzen Satz.
17. Alex: Und noch die zwei.
18. Interviewerin: Ja. Aber jetzt nochmal alles als Satz formuliert.
19. Simon: Die fünf Punkte hier oben bleiben immer gleich.
20. Interviewerin: Genau, vielleicht kannst du auch noch sagen, in einer Spalte. Ne? Fünf Punkte in einer Spalte bleiben immer gleich. Und was passiert von Bild zu Bild? Was passiert da?
21. Alex:Bleibt auch immer gleich, außer die zwei.
22. Interviewerin: Genau, es wird immer – so kann man es auch sagen – zwei größer oder vermehrt sich um zwei.
Im Materialteil finden Sie u. a. eine Verlinkung zum Sprachförderfilm unseres Partnerprojekts PIK AS, in dem Sie sehen können, wie in einem sprachlich sehr schwachen zweiten Schuljahr der Aufbau der Hundertertafel sprachsensibel behandelt wird.
Im Unterrichtsteil wird nun das Makro-Scaffolding mehr in den Blick genommen, d. h. es wird der Frage nachgegangen, welche sprachlichen Unterstützungmöglichkeiten Sie bei der Unterrichtsplanung gezielt berücksichtigen können.