In der Individualisierungsfalle
In den letzten Jahren hat sich u. a. im Zuge dessen, dass die Grundschule als inklusiver Lern- und Förderort für alle Kinder verstanden wird, auch der Unterricht verändert. Vielfach wird er differenzierter angelegt, indem z. B. vermehrt auch Aspekte der Sprachförderung und der Adaption von Aufgaben berücksichtigt werden.
Allerdings ist auch die wachsende Tendenz zu beobachten, dass die Lernenden sich den ‚Stoff’ mit Hilfe eines Schulbuches oder einer Fülle von durch die Lehrperson zusammen gestellten Arbeitsblättern selbst erarbeiten sollen. Hier müssen sich die Lernenden die Lerninhalte im Wesentlichen individualisiert, häufig ohne Austausch mit anderen aneignen – oft kleinschrittig, mit reduziertem fachlichem Anspruch und auch weitgehend ohne Berücksichtigung der prozessbezogenen Kompetenzen.
Diese Form von Mathematikunterricht mag zwar manchmal angesichts schwieriger Rahmenbedingungen aus unterrichtsorganisatorischer Sicht verständlich sein, ist aber in der Regel nicht nur für die Motivation der Kinder, sondern auch für deren mathematische Lernentwicklung als problematisch zu bezeichnen. Unterricht tappt so in die sog. Individualisierungsfalle: Individualisierung in Form eines nebeneinanderher Arbeitens, weitgehend ohne fachbezogene Gespräche und ohne den Einsatz der Lernkatalysatoren Kommunikation und Kooperation.
Formen des Lernens von- und miteinander

Somit ist es wichtig, im Unterricht immer auch die kontinuierliche Anregung zu sachbezogenem und lernförderlichem Austausch, zum einen mit Mitlernenden aber auch mit der Lehrperson, sicherzustellen.
Lernen von- und miteinander kann dabei durch unterschiedliche Methoden im Unterricht initiiert bzw. durch verschiedenen Kooperationsformen realisiert werden. Kinder können in Partnerarbeit, in verschiedenen Formen der Gruppenarbeit oder in sogenannte Mathekonferenzen (siehe Protokoll in der Abb. oben) durch bzw. im Austausch mit anderen Kindern Aufgabenstellungen gemeinsam bearbeiten und mathematikhaltige Probleme lösen, vgl. auch pikas.dzlm.de.
Dabei müssen sie ihre eigenen, individuellen Denkweisen oder Lösungswege entwickeln, diese dann aber auch mit denen anderer in Beziehung setzen, über diese diskutieren und für Problemlösungen miteinander vergleichen und bewerten. In diesem Prozess werden die Kinder angeregt zu argumentieren, sich auf andere Sichtweise einlassen und dringen so tiefer in mathematische Sachverhalte ein. So werden sich die Kinder des eigenen Lernens bewusster, erweitern die eigenen Denk- und Vorgehensweisen auch kontinuierlich bzw. grenzen sie von anderen (evtl. falschen) ab und werden so flexibler.
Die Aufgabenauswahl spielt eine wichtige Rolle. Ein Austausch ist besonders dann sinnvoll und ergiebig, wenn die Aufgabe unterschiedliche Denk- und Vorgehensweisen zulässt und überhaupt auch einen wechselseitigen Austausch fordert. Gerade zu leichte oder zu wenig komplexe Aufgaben bergen die Gefahr, das Kinder sie nicht gemeinsam bearbeiten, da sie schneller und effektiver in Einzelarbeit gelöst werden können (Nührenbörger/ Verboom 2005).
Je nach Aufgabenstellung und der zu fördernden Kompetenzen müssen die unterschiedlichen Formen somit zielgerichtet ausgesucht und eingesetzt werden. Denn je nach Lernumgebung oder Aufgabenstellung eignet es sich, diese evtl. nicht in einem (direkten) Austausch mit anderen zu erarbeiten oder eben nur mit einem Partner statt in einer großen Gruppe.
Oft ist es sinnvoll, den Kindern vorab eine Phase der eigenständigen Auseinandersetzung zu ermöglichen, um sich im eigenen Tempo auf die mathematisch Aufgabenstellung einzulassen und erste Denk- und Vorgehensweise zu entwickeln. Nach dem „Ich-Du-Wir-Prinzip“ wechseln so Phasen des individuellen Lernens mit denen des gemeinsamen Austausches. Phasen des individualisierten Lernens haben also in diesem Kontext zu Recht ihren Platz, aber sie sollten eben den Unterricht nicht dominieren.
Die Bedeutung gemeinsamer Reflexionsphasen
Sowohl nach der Arbeit in Partner- oder Gruppenarbeit oder nach dem Abhalten von Mathekonferenzen spielen gemeinsame Reflexionsphase eine zentrale Rolle. Die Lehrkraft sollte bereits in den gemeinsamen Arbeitsphasen die für sie „freie Zeit“ nutzen, um Einblicke in den (produktiven) Austausch der Kinder zu bekommen. Aufgabe der Lehrkraft in den gemeinsamen Reflexionsphasen ist es dann, das dort Erarbeitete zu bündeln und in Bezug auf eine gemeinsame Reflexionsfrage zentralen Lerngelegenheiten fokussiert in den Blick zu nehmen und diese herauszuarbeiten (vgl. Sundermann & Selter, 2017).
Dies kann sich durchaus auch auf die Metaebene der gemeinsamen Arbeit beziehen oder auf Rückmeldung zu gestalterischen Kriterien erarbeiteter Arbeits-/Lösungsdokumentationen („(Wie) kann man auf dem Plakat erkennen, was die Kinder herausgefunden haben? Welche Tipps habt ihr an die Gruppe?)“.
Wichtig hierbei ist es, die Kinder und ihre Arbeitsergebnisse miteinzubeziehen und sie erneut (meist in anderen Konstellationen) in den Austausch zu bringen. Dabei werden die Kinder angehalten, ihren Lernprozess selbst resümieren, um das Gelernte zu festigen, aber es werden vor allem dabei auch ihre argumentativen und kommunikativen Kompetenzen erneut herausgefordert und gefördert. Die Lehrkraft kann dabei erweitern, ergänzen und durch gezielte Impulse und Fragestellungen den initiierten Lernzuwachs sichern (oder eben ausmachen, an welchen Stellen erneut angesetzt werden muss).
Das Lernen von- und miteinander lernen
Auch das gemeinsame Arbeiten ist ein Lernprozess, in dem sich die Kinder stetig üben müssen, damit produktive Lerngelegenheiten entstehen können. Dabei benötigen die Kinder Unterstützung, sodass gemeinsame Arbeitsphase von der Lehrkraft (nicht nur zu Beginn) gut durchdacht und (vor)strukturiert werden müssen. Klare Arbeitsanweisungen und Fragestellungen sind dabei genauso wichtig wie die Bereitstellung grundlegenden und weiterführenden Materialien (didaktische Materialien, Darstellungsformen) oder anderer Unterstützungsmöglichkeiten (Tippkarten o.ä.).
Natürlich suchen die Kinder sich am liebsten ihre eigenen Partner oder Gruppenmitglieder aus. Im Sinne der Motivation und auch in Bezug darauf, dass in diesen Konstellationen oft die Hemmschwelle gemeinsam zu diskutieren geringer ist, als mit Kindern zusammen zu arbeiten, die man nicht so gut kennt oder nicht mag, ist dies nicht immer ein Garant für die Produktivität und der Qualität des Austausches.
So ist es durchaus sinnvoll, dass Partnerteams und Gruppen auch mal von der Lehrkraft zusammengestellt werden. Dabei ist nicht die Homogenisierung der Tandems oder Gruppen das Ziel, vielmehr sollte sich die Zusammenstellung in Bezug auf das Ziel und sich eventuell ergänzenden Kompetenzen der einzelnen Kinder orientieren.
Eine der Methoden zur kontinuierlichen Anregung zu sachbezogenem und lernförderlichem Austausch mit Mitlernenden, also zum Lernen von- und miteinander, stellen die sog. Mathe-Konferenzendar. An diesem Beispiel können alle vorab angesprochenen Ausführungen konkretisiert werden.
Begriffliches zu Mathe-Konferenzen
Als Rechen- oder Mathe-Konferenz bezeichnet man einen Zusammenschluss von Kindern in (heterogenen) Kleingruppen zur Vorstellung und Reflexion von individuellen Lösungswegen im Mathematikunterricht (vgl. Sundermann & Selter 2012; vgl. im Weiteren pikas.dzlm.de/394).

In diesen Kleingruppen treten die Kinder über mathematische Sachverhalte in einen mündlichen Austausch. Es geht vor allem darum, die sachbezogene Kommunikation untereinander sowie das Lernen von- und miteinander zu fördern: Wesentlich ist, dass im Rahmen der Mathe-Konferenz die Schüleraktivitäten und Ergebnisse der Schülerinnen und Schüler zusammengeführt und die Prozesse reflektiert werden. Die Kinder werden herausgefordert, ihr Vorgehen bei der Lösung einer Aufgabe oder ihre Entdeckungen zu beschreiben und zu begründen sowie die Gedankengänge ihrer Mitschülerinnen und Mitschüler nachzuvollziehen.
Neben der kommunikativen Kompetenz werden zudem auch die darstellenden und argumentativen Kompetenzen der Lernenden gefordert und gefördert, indem sie unter anderem ihre unterschiedlichen Lösungswege präsentieren, vergleichen und konstruktiv bewerten. In diesem Sinne tragen Mathe-Konferenzen zur Entwicklung einer Kultur des Verstehens und Verstandenwerdens bei.
Vorteile
Von diesem sachbezogenen Austausch können alle Schülerinnen und Schüler profitieren, so dass der Mathe-Konferenz eine Doppelfunktion zukommt: Einerseits profitieren die Kinder, die ihre Lösungswege erklären, indem sie ihr Vorgehen und ihre eigenen Gedankengänge verbalisieren und versuchen, diese verständlich zu präsentieren. Andererseits werden gleichzeitig die zuhörenden Kinder aktiv miteinbezogen, indem sie die Vorgehensweisen anderer nachvollziehen und vergleichen sollen, um anschließend kriteriengeleitet Rückmeldungen geben zu können.
Zugleich werden somit Lösungswege und Lösungen überprüft und ggf. können die Kinder gemeinsam nach den Ursachen von Fehlern suchen sowie erste Vorschläge zur Weiterentwicklung und zum Weiterdenken entwickeln. Gegenüber einer Reflexionsphase im Plenum wird durch diese Kooperationsform die sprachliche Beteiligung (und die Auseinandersetzung mit der gestellten Aufgabe) des einzelnen Kindes erhöht, auch schwächere und weniger mitteilsame Kinder können leichter zu Wort kommen.
Eine Reflexionsphase im Plenum wird durch die Durchführung von Mathe-Konferenzen natürlich nicht überflüssig, sondern kann im Gegenteil durch diese besonders gut vorbereitet werden. Und: Auch die ‚stilleren‘ Kinder werden ggf. durch den Rückhalt der Kleingruppe ermutigt, ihre Gedanken zu artikulieren.
Voraussetzungen
Die Methode ‚Mathe-Konferenz’ kann bereits im ersten Schuljahr eingeführt werden. Wesentliche inhaltliche Voraussetzung für die Durchführung von Mathe-Konferenzen ist die Ergiebigkeit der Aufgabe. Diese muss mathematisch anspruchsvoll genug sein, also auch prozessbezogene Kompetenzen berücksichtigen, und unterschiedliche Denk- und Lösungswege zulassen, so dass ein Austausch auch aus der Sicht der Kinder sinnvoll wird.
So können verschiedene Lösungswege zu einer Aufgabe, entdeckte Muster und Strukturen oder das Finden einer möglichst geschickten Strategie Gegenstände einer Mathe-Konferenz sein (vgl. z.B. pikas.dzlm.de/091, pikas.dzlm.de/008 oder pikas.dzlm.de/170).
Die Fähigkeit, sich an Mathe-Konferenzen zu beteiligen, eigene Ergebnisse und Vorgehensweisen zu erklären und Ideen und Lösungswege anderer nachzuvollziehen, entwickelt sich bei den Kindern allerdings nicht von selbst. Wie jede andere Methode, muss daher auch die Mathe-Konferenz zunächst eingeführt und ritualisiert werden, so dass sie sich im Laufe der Zeit als gängige Methode in der Klasse etablieren kann.
Wie kann es gehen?
Zur Strukturierung der Auseinandersetzung mit ergiebigen, ‚guten‘ Aufgaben kann der gesamte Prozess im Sinne des kooperativen Lernens in drei Phasen untergliedert werden:
1. die sog. ‚Ich- Phase‘,
2. die ‚Du-Phase‘
3. die ‚Wir-Phase‘
(vgl. zum ‚Ich-Du-Wir-Prinzip‘ auch die weiterführenden Informationen unter pikas.dzlm.de/058 sowie Gallin & Ruf 1998).
Diese drei Phasen können Sie mit Hilfe des Übersichts-Plakates (Mathe-Aufgaben gemeinsam lösen. Leitfaden: 1. Ich 2. Du 3. Wir) für Ihre Schülerinnen und Schülern transparent machen.
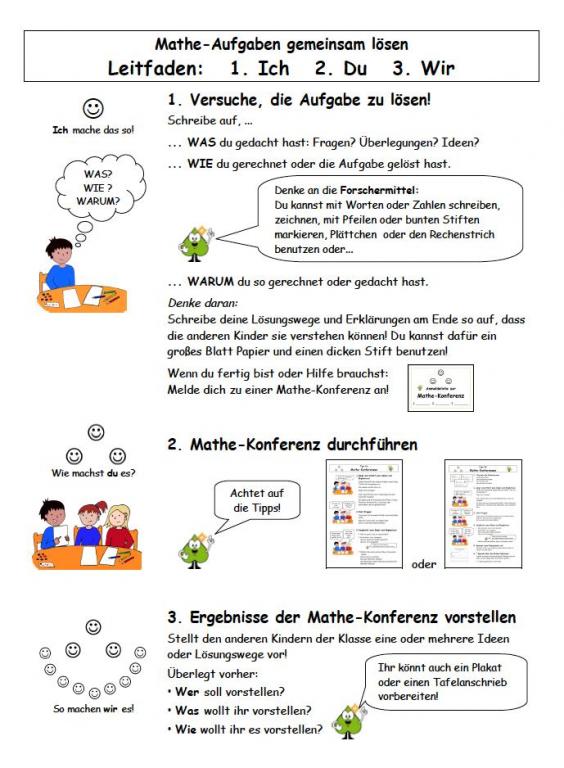
Viele, weitere unterrichtliche Einsatzmöglichkeiten konkretisierende und direkt in Unterricht und Fortbildung einsetzbare Materialien finden Sie auf der Website unseres Partnerprojekts PIKAS.
Material