Stochastik in der Grundschule? Ja, aber was und wie?
Auf dieser Seite werden zur Leitidee
Daten und Zufall zu folgenden zentralen Punkten Hintergrundinformationen gegeben:
Unfassbare, unsichere und unerklärliche Ereignisse werden oft mit Zufall in Verbindung gebracht. So entwickeln bereits Kinder Vorstellungen darüber, was Zufall ist.
Pauls Antwort darauf ist:
Zufallsbegriff
Von Zufall spricht man dann, wenn für ein einzelnes Ereignis oder das Zusammentreffen von mehreren Ereignissen keine kausale Erklärung gegeben werden kann.
Dabei ist charakteristisch, dass
-
bei gleicher Ausgangssituation mehrere Endsituationen (Ereignisse) möglich sind und
-
bei Wiederholung der gleichen Ausgangssituation ein anderes Ereignis eintreten kann.
Eigenaktivität
Stellen Sie sich vor, Sie würden vierundzwanzig Mal eine Münze werfen. Als Ergebnis erhalten Sie entweder Zahl (Z) oder Wappen (W). Ihre (gedanklichen) Wurfergebnisse notieren Sie bitte in einer Tabelle folgender Form.
Die Aufgabenstellung ist klar? - Dann werfen Sie JETZT gedanklich so schnell wie möglich eine Münze vierundzwanzig Mal. Für Zahl tragen Sie Z, für Wappen entsprechend W in Ihre Tabelle ein.
Insbesondere die Erfahrungen der Kinder mit Würfelspielen, die in der Regel auch emotional geprägt sind, führen oft zu fehlerhaften Erklärungsmustern und Fehlvorstellungen über Zufall. Die Herausforderung für den Grundschulunterrricht besteht darin, Fehlvorstellungen und fehlerhafte Erklärungsmuster der Kinder zumindest zu erschüttern. Um den Zufall zu verstehen, müssen Zufallsversuche von Kindern selbst durchgeführt und reflektiert werden.
Wahrscheinlichkeitsbegriff
Mit der Angabe der Wahrscheinlichkeit versucht man die Unsicherheit von Ereignissen zu beschreiben und zu erklären. Als ein quantitatives Maß gibt sie an, wie gewiss es ist, dass ein bestimmtes Ereignis eintreten wird.
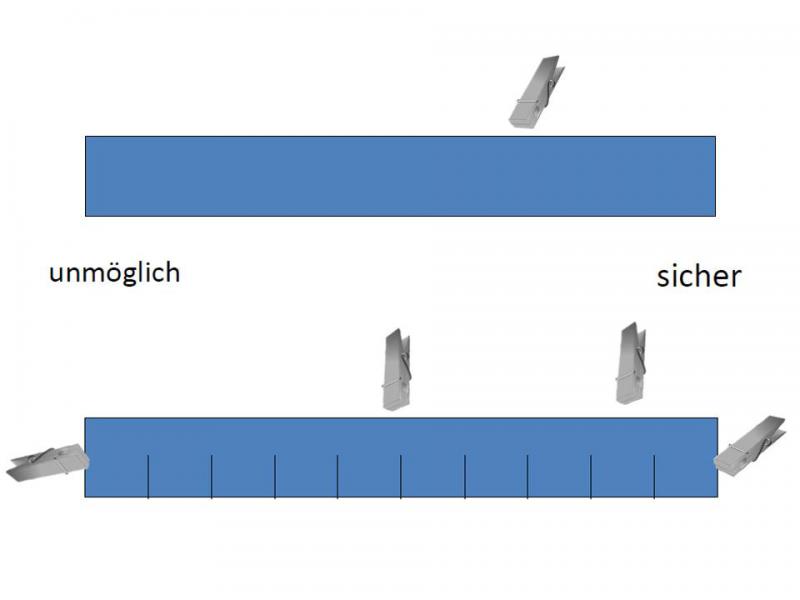
Auch Grundschulkinder können bereits die Unsicherheit von Ereignissen beschreiben. Ereignisse aus ihrer Erfahrungswelt können sie als unmöglich, möglich oder (ganz) sicher einschätzen.
Mit Hilfe eines Pappstreifens und einer Klammer können sie veranschaulichen und begründen, ob sie mögliche Ereignisse eher für unmöglich oder sicher halten oder auch als fifty-fifty einschätzen.
Damit werden Kinder angeregt, Wahrscheinlichkeiten quantitativ abzuschätzen und können dazu ein erstes inhaltliches Verständnis erwerben.
Laplace-Wahrscheinlichkeit
Die Ereignisse besitzen gleiche Eintrittswahrscheinlichkeiten. Die Wahrscheinlichkeit eines Ereignisses ist das Verhältnis der Anzahl der günstigen Ergebnisse zur Gesamtzahl der Ergebnisse.
Dieser klassische Wahrscheinlichkeitsbegriff wurde von Laplace definiert und in der Folge als Laplace-Wahrscheinlichkeit bezeichnet.
Beispiel: Werfen eines Würfels
Da der Würfel symmetrisch ist, nimmt man an, dass das Eintreffen der Augenzahlen 1 bis 6 gleichwahrscheinlich ist. Die Wahrscheinlichkeit für das Ereignis "Werfen einer geraden Zahl" bestimmt sich aus dem Verhältnis
... der Anzahl der günstigen Ergebnisse: 3 (Augenzahlen 2, 4 und 6)
... zur Gesamtzahl der Ergebnisse: 6 (Augenzahlen 1, 2, 3, 4, 5, 6)
Damit ist die Wahrscheinlichkeit (P) für das Ereignis (E) "Werfen einer geraden Zahl"
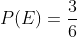
Was bedeutet das für das Arbeiten im Mathematikunterricht der Grundschule?
Die Kinder erkennen frühzeitig die Symmetrie des Würfels und sie leiten daraus auch ab, dass der Würfel "...deswegen auch beim Werfen auf jede Fläche fallen kann." Die Kinder können für dieses Beispiel die "richtigen" (günstigen) Würfe und auch die Anzahl der möglichen Würfe benennen. Derartige Betrachtungen und Aussagen zu Spielverläufen tragen dazu bei, dass Kinder im Grundschulalter ein inhaltliches Verständnis von (Laplace-)Wahrscheinlichkeit entwickeln.
Statistische Wahrscheinlichkeit
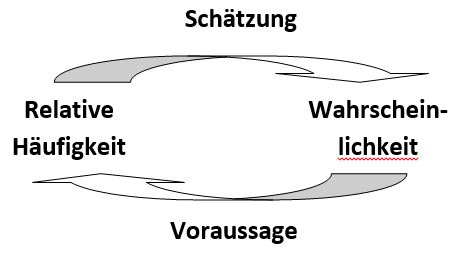
Im Unterschied zur Laplace-Wahrscheinlichkeit gibt es auch Elementarereignisse, die nicht die gleiche Eintrittswahrscheinlichkeiten haben.
Wenn Zufallsversuche unter gleichen Bedingungen oft genug wiederholt werden, kann die relative Häufigkeit als Schätzwert für die Wahrscheinlichkeit des Eintreffens eines Ereignisses verwendet werden. Andererseits kann die Wahrscheinlichkeit zur Voraussage über die relative Häufigkeit des Eintreffens eines Ereignisses genutzt werden.
Dazu gehören beispielsweise Wetterprognosen: Eine Vielzahl von Wetterdaten (Temperatur, Luftdruck, Niederschlagsmengen, Windgeschwindigkeit, ...) werden an den verschiedensten Orten der Welt mehrmals täglich und seit Jahrzehnten gesammelt. Im Ergebnis der Aufbereitung und Interpretation dieser Daten wurden verschiedene Wettermodelle geschaffen, die entsprechend aktueller Daten geprüft und gegebenenfalls angepasst werden. Die relativen Häufigkeiten liefern Schätzwerte für die Wahrscheinlichkeit des Eintreffens bestimmter Wetterphänomene, die u. a. als Wettervorhersagen Bestandteil des täglichen Wetterberichts sind.
Mit jüngeren Grundschulkindern wird in der Regel der (Zufallsgenerator) Würfel untersucht. Wir möchten Sie ermutern, älteren Grundschulkindern die Chance zu geben, andere Körper (s. Abb.) zu untersuchen, um ihr Verständnis von Wahrscheinlichkeit zu erweitern.
Eigenaktivität
Wählen Sie drei Körper aus und beantworten Sie folgende Frage:
Wie groß ist die Wahrscheinlichkeit dass eine Sechs geworfen wird? Welchen Körper Ihrer Auswahl würden Sie als "Spielwürfel" bevorzugen?
Begründen Sie Ihre Entscheidung. Dokumentieren Sie Ihr Vorgehen und Ihre Überlegungen.


Fordern Sie Ihre Kinder zunächst auf, ihre Erwartungen zu beschreiben, eine Prognose zu formulieren und diese zu begründen. Geben Sie den Kinder die Möglichkeit, ihre Aussagen experimentell zu überprüfen. Durch eine große Anzahl von Würfen sind relative Häufigkeiten zu ermitteln. Nur auf dieser Grundlage können in diesem Fall Aussagen getroffen und die Wahrscheinlichkeiten geschätzt werden. Diese sollten im Anschluss mit den Prognose verglichen werden.
Was bedeutet das für das Arbeiten im Mathematikunterricht der Grundschule?
Wie im vorangegangenen Beispiel exemplarisch dargestellt, werden bei Untersuchungen von Zufallsgeneratoren folgende Arbeitsschritte durchlaufen:
-
Erwartungen formulieren und begründen,
-
experimentell arbeiten,
-
Ergebnisse interpretieren und
-
mit dem Erwartungsbild vergleichen.
Dieses Arbeiten können bereits Grundschulkinder erlernen. Wenn Kindern immer wieder die Möglichkeit gegeben wird, sich in dieser Art und Weise mit Zufallsversuchen auseinanderzusetzen, entwickeln sich ihre stochastischen Denk- und Arbeitenweisen.
Bestimmung der Gesamtzahl der Ergebnisse - kombinatorische Überlegungen
Um Wahrscheinlichkeitsaussagen treffen zu können, ist die Bestimmung der Gesamtzahl der möglichen Ergebnisse notwendig. Es ist zu ermitteln, welche Möglichkeiten und wie viele es gibt. Dazu sind kombinatorische Überlegungen anzustellen.
„Kombinatorik ist die Kunst des geschickten Zählens" (Hefendehl-Hebeker 2003).
Der Link zu KIRA: Daten, Häufigkeiten und Wahrscheinlichkeiten – Kombinatorik gibt Ihnen die Möglichkeit, sich zum Thema Geschicktes Zählen weiter zu informieren.
Als weiteren Weg zur Ermittlung der Gesamtzahl möchten wir die Nutzung von Baumdiagrammen beispielhaft darstellen. Ein typisches kombinatorisches Problem, das bereits im Anfangsunterricht genutzt wird, ist eine Anziehaufgabe. Fachwissenschaftlich ist eine derartige Aufgaben eine Permutation ohne Wiederholung.
Aufgabe
Paula hat eine gelbe und eine rote Mütze, eine rote, eine blaue und eine grüne Jacke und rote und schwarze Stiefel. Wie könnte Paula ihre Kleidungsstücke miteinander kombinieren? Finde verschiedene Möglichkeiten.
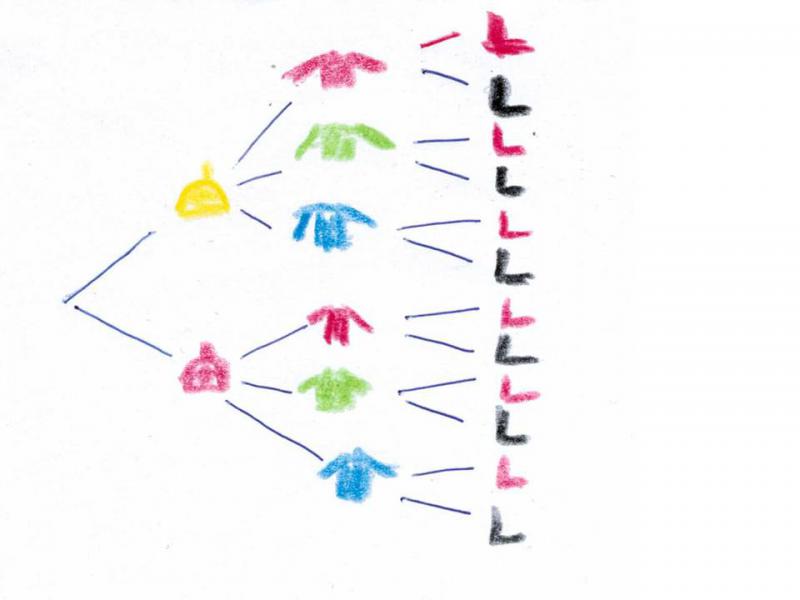
Bilder helfen Kombinationen zu legen und viele, vielleicht auch alle Möglichkeiten zu finden.
Ein Baumdiagramm kann das Vorgehen und die gefundenen Möglichkeiten veranschaulichen. Diese Dokumentation ist geeignet, weitere Fragen zu beantworten und Aussagen zu treffen.
So können Kinder prüfen, ob es weitere Möglichkeiten gibt bzw. ob sogar alle Möglichkeiten gefunden wurden. Es kann eine Aussage darüber getroffen werden, wie viele Möglichkeiten es gibt, dass ein grüner Pullover angezogen wird und welche Kombinationen mit einem grünen Pullover möglich sind.
Als Hilfsmittel kann diese Darstellung von Kindern in der Kommunikation und beim Argumentieren genutzt werden.
Eigenaktivität
Erstellen Sie zu dieser Aufgabe mindestens ein weiteres Baumdiagramm. Beginnen Sie zunächst mit den Jacken.
Überlegen Sie, wie mit Grundschulkindern diese verschiedenen Baumdiagramme untersucht werden können.
Grundschulkinder können auch einfache mehrstufige Zufallsversuche durchführen. Mithilfe eines Baumdiagramms können Überlegungen zum Versuchsverlauf dokumentiert und Wahrscheinlichkeitsaussagen getroffen und begründet werden.
Beispielaufgabe zum klassischen Spielwürfel (Zweistufiger Zufallsversuch):
Wie wahrscheinlich ist es, dass ich bei aufeinanderfolgenden Würfen jeweils eine Sechs erhalte?
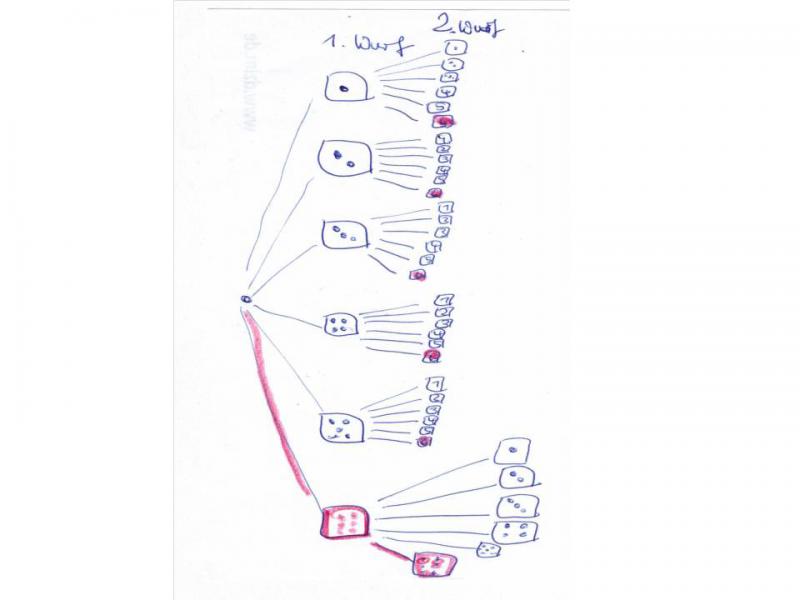
Ein Kind hat in einem Baumdiagramm seine Überlegungen notiert. In einem ersten Schritt hat es die Möglichkeiten des 1. Wurfs aufgezeichnet. Im Weiteren aber zunächst nur noch den Pfad der Sechs vervollständigt. Danach hat es oben angefangen, die Möglichkeiten für den 2. Wurf zu zeichnen.
Bereits nach den ersten drei Würfelbildern hat es ein Muster erkannt - "es geht immer gleich weiter" - und ist zur Ziffernschreibweise übergegangen. Das Kind brachte zudem zum Ausdruck, dass es das Baumdiagramm nur vervollständigt, damit alle Kinder sehen können es "geht auch wirklich immer gleich weiter". Farblich wurde die Sechs hervorgehoben, um auf die Ausgangsfrage Bezug zu nehmen.
Die Lerngruppe nutzte diese Darstellung für einen weiteren Austausch zur Fragestellung. Die Kinder schätzten ein, dass die Wahrscheinlichkeit eines Wurfs "6/6" eigentlich klein ist, da es ja nur eine von insgesamt 36 Möglichkeiten ist.
Sie thematisierten auch, dass es im Spiel (Experiment) aber doch schon vorkommen kann, dass mehrfach "6/6" geworfen wird.
Das gewählte Beispiel zeigt auch Grenzen einer Darstellung im Baumdiagramm. Bei vielen möglichen Ergebnissen und Versuchen mit weiteren Stufen wird die Darstellung im Baumdiagramm unübersichtlich. Das sollte man bei der Aufgabenstellung bzw. Auswahl und Entwicklung von Aufgaben beachten.
Was bedeutet das für das Arbeiten im Mathematikunterricht der Grundschule?
Bereits in der Grundschule ist ein Baumdiagramm geeignet, Überlegungen zu Zufallsversuchen zu veranschaulichen und die Anzahl günstiger und möglicher Ergebnisse abzulesen.
Diese Form der Dokumentation unterstützt Kommunikationen und Argumentationen zu zufälligen Ereignissen und Wahrscheinlichkeitsaussagen.
Im Würfel-Beispiel wird zudem ersichtlich, dass bereits der Einstieg in die Darstellung eines Baumdiagramms das Erkennen von Mustern und Strukturen unterstützt.
Damit wird die Entwicklung eines Verständisses von zufälligen Ereignissen und grundlegenden Begriffen und Gesetzmäßigkeiten der Wahrscheinlichkeitsrechnung bei Grundschulkindern gefördert.
In einer Übersicht finden Sie mathematische Fachbegriffe aus der Kombinatorik: Ihnen wurden illustrierende Aufgabenbeispiele für die Grundschule zugeordnet.
Wahrscheinlichkeit und Chance
Gelegentlich wird neben dem Begriff Wahrscheinlichkeit auch der Begriff Chancen verwendet. So spricht man oft im Zusammenhang mit Spielen von Gewinnchancen.
Wahrscheinlichkeit und Chance sind beide geeignet, das Eintreffen eines Ereignisses quantitativ zu charakterisieren. Beide unterscheiden sich in der Art und Weise der Beschreibung. Bei der Verwendung der Begriffe im Unterricht sollten die Unterschiede in der Beschreibung herausgearbeit werden.
Folgende Tabelle stellt die beiden Begrifflichkeiten am Beispiel der Wahrscheinlichkeit und der Chance, die Augenzahlen 1 und 6 zu würfeln, dar.
Wahrscheinlichkeit
Verhältnis von Anzahl der günstigen zur Anzahl aller möglichen Ereignisse
Günstige Ereignisse: 2 (Augenzahl 1 und 6)
Mögliche Ereignisse: 6 (Augenzahl 1 - 6)
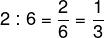 (für Bruchrechnung nutzbar - Anteile)
(für Bruchrechnung nutzbar - Anteile)
Chance
Verhältnis von Anzahl der günstigen zur Anzahl der ungünstigen Ereignissen
Günstige Ereignisse: 2 (Augenzahl 1 und 6)
Ungünstige Ereignisse: 4 (Augenzahlen 2 - 5)
2 : 4
(2 zu 4 - Verhältnis)
Bisher wurden fachliche Hintergrundinformationen gegeben und mit einigen Beispielen illustriert. Auf der folgenden Seite wollen wir versuchen exemplarisch zu veranschaulichen, wie es im Unterricht gelingen kann, ein inhaltliches Verständnis von Zufall und Wahrscheinlichkeit zu entwickeln.