Unterricht

Wie gelingt es, ein inhaltliches Verständnis von Zufall und Wahrscheinlichkeit zu entwickeln?

Für einen Zugang zur Thematik "Zufall und Wahrscheinlichkeit" können die vielfältigen Erfahrungen der Kinder mit Spielen genutzt werden.

Du hast vier Mal eine Sechs gewürfelt? Du schummelst!

oder

Es ist richtig schwer, eine Sechs zu würfeln.

Solche oder ähnliche Aussagen der Kinder können Ausgangspunkt sein, den Zufallsgenerator Würfel näher zu untersuchen. Dabei geht es um Lernumgebungen, die Kinder zu einem reflektierten Umgang mit Glücksspielen und Wahrscheinlichkeitseinschätzungen anregen sollen.

In einem ersten Schritt sollten die Kinder ihre Erfahrungen mit dem Würfeln und ihre Erwartungen an eine experimentelle Untersuchung zum Ausdruck bringen. Oft werden typische Fehlvorstellungen (wie bereits oben genannt) sichtbar oder auch weitere, wie
... es fiel drei Mal die Sechs, jetzt sind die Sechsen raus.
... es fiel drei Mal die Sechs, also ist das ein Sechser-Würfel.

Diese Auffassungen, die erfahrungsbasiert und in der Regel auch emotional geprägt sind, können nur durch experimentelles Arbeiten und das bewusste Reflektieren der Ergebnisse erschüttert werden. Aus diesem Grund sollten Sie vor Versuchsbeginn durch die Kinder unbedingt dokumentiert werden.
Ein Auftrag fordert die Kinder auf, einen Würfel-Versuch durchzuführen und die Ergebnisse zu dokumentieren. An dieser Stelle wird auf ein Beispiel von PIKAS (PIKAS: Unterrichtsmodul: Daten, Häufigkeiten und Wahrscheinlichkeiten – Wahrscheinlichkeiten – Zufallsexperimente) Bezug genommen (vgl. PIK AS o. J.).

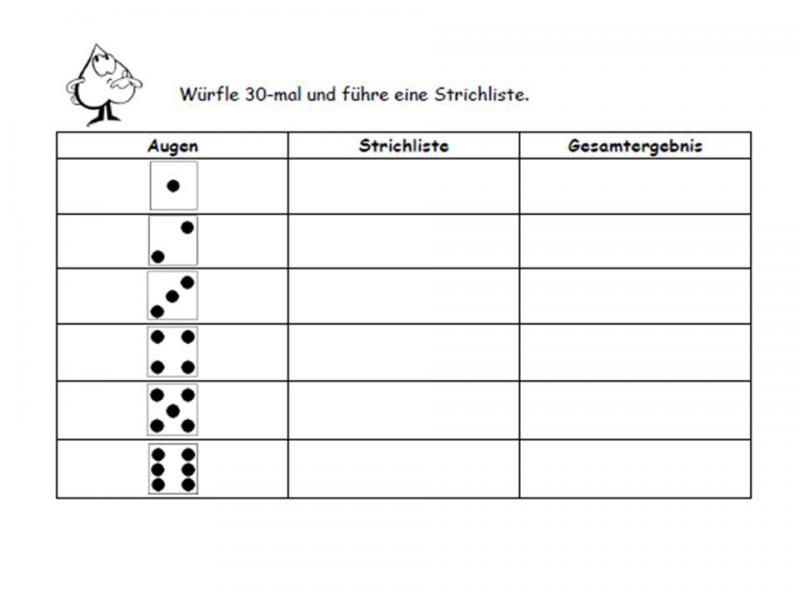
• Was fällt dir auf, wenn du die Gesamtergebnisse vergleichst?
• Versuche deine Entdeckungen zu erklären.

Im nächsten Schritt sind Auffälligkeiten zu beschreiben, über mögliche Erklärungen nachzudenken und die Ergebnisse mit den Erwartungen zu vergleichen.
Diese Schülerlösungen bieten die Chance mit den Kindern ins Gespräch zu kommen.

Dieses Kind schließt aus den eigenen Versuchserfahrungen auf die Allgemeingültigkeit:

Eine Aussage, die Nachfragen provoziert:

Sie können sich diese und weitere Schülerlösungen und Informationen dazu anschauen: PIKAS: Unterrichtsmodul: Daten, Häufigkeiten und Wahrscheinlichkeiten – Wahrscheinlichkeiten – Zufallsexperimente.

Die ausgewählten Schülerlösungen unterscheiden sich in der Qualität und Quantität der Beschreibungen. Sie ermöglichen es, artikulierte Fehlvorstellungen zu hinterfragen, auf der Grundlage der konkreten Versuchsergebnisse zu diskutieren und typische Phänomene des Zufalls anzusprechen.
Dazu gehören zum Beispiel:

• Auch dem Zufall liegt auf lange Sicht (über viele Versuche hinweg) eine "Gesetzmäßigkeit" zugrunde.
• Trotzdem kann man nicht vorhersagen, was im nächsten Versuch kommt.

Wenn Kinder die Chance haben, entsprechend zu arbeiten, lernen sie grundlegende stochastische Arbeitsweisen kennen und nutzen. Das unterstützt die Entwicklung stochastischen Denkens.