Zählendes Rechnen
Bevor darüber nachgedacht werden kann, ob, warum und wie die Ablösung vom zählenden Rechnen gelingen kann, soll zunächst folgendes geklärt werden:
Was ist zählendes Rechnen?
Das verfestigte zählende Rechnen gilt als ein deutliches Anzeichen für besondere Probleme beim Rechnenlernen – und es ist auch ein Hauptgrund für besondere Probleme beim Rechnenlernen. Streng genommen handelt es sich beim „zählenden Rechnen“ auch gar nicht um Rechnen – sondern um die zählende Ermittlung von Lösungen gegebener Plus- und Minusaufgaben.
Zugespitzt bedeutet dies: „Rechenschwache“ Kinder rechnen nicht – sie zählen (Gaidoschik 2011, S. 32).
Um den Unterschied zwischen „zählendem Rechnen“ und „Rechnen“ zu verdeutlichen, lassen Sie sich bitte auf folgende Aufgabe ein:
Eigenaktivität
Bitte rechnen Sie die Aufgabe 63-28 – am besten im Kopf.
Bitte überlegen Sie sich dabei sehr genau, was während des Rechnens „in ihrem Kopf vorgeht“ und notieren Sie ihren Rechenweg möglichst detailliert.
Fällt Ihnen noch eine andere Möglichkeit ein? Können Sie diese auch notieren?
Sie werden vielleicht gemerkt haben, dass Sie beim Rechnen sehr viele unterschiedliche „mentale Werkzeuge“ nutzen (zum Beispiel auswendig genutzte Aufgaben, Rechengesetze, Ihr Wissen über das Stellenwertsystem, Ihr Wissen über die zugrundeliegende Operation, Ihr Wissen über Zahlbeziehungen, ...).
Was genau dieses „mentale Werkzeug“ ist, und wie es beim Rechnen genutzt wird finden Sie weiter unten.
Einen anderen Lösungsweg schlägt der Drittklässler Peter ein:
Peter: 63 minus 28. Ok also erstmal sechs minus zwei... sind...
(er flüstert "sechs, fünf, vier" und streckt bei den Zahlwörtern fünf und vier jeweils einen Finger aus)
... vier. Also erstmal vier hierhin.
(er notiert die 4 hinter dem Gleichheitszeichen)
Dann noch acht minus drei ... sind ...
(er flüstert erneut, diesmal kaum hörbar und streckt dabei nacheinander drei Finder aus)
... sechs ...? Ja, sechs.
(er notiert die 6 hinter der bereits notierten 4)
Das sind dann sechsundvierzig.
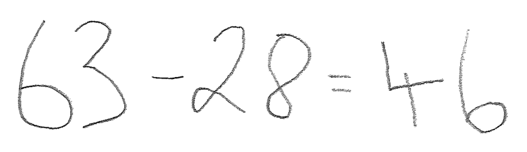
Offensichtlich benutzt Peter grundsätzlich anderes „Werkzeug“ als Sie beim Lösen der Aufgabe 63-28 – und das von ihm genutzte Werkzeug scheint nicht besonders tragfähig zu sein.
Die zählende Lösung von einfachen Additions- und Subtraktionsaufgaben ist zu Beginn der Grundschulzeit ein ganz normales und erwartbares Vorgehen – viele Kinder können in der Regel zu diesem Zeitpunkt kaum andere Strategien zur Lösung solcher Aufgaben nutzen (vgl. Gaidoschik 2010).
Manche Aufgaben werden von einigen Kindern jedoch auch schon auswendig gewusst – zum Beispiel die Verdopplungsaufgaben ohne Zehnerübergang (2+2, 3+3, 4+4, 5+5) oder solche Aufgaben, bei denen nur Eins addiert wird (z. B. 6+1) (vgl. Gaidoschik 2010, S. 329).
Aber auch diese Aufgaben werden längst nicht von allen Schulanfängerinnen und -anfängern auswendig gewusst – so ist das zählende Rechnen bei der Aufgabe 4+4 eine häufig anzutreffende Lösungsstrategie (vgl. ebd.).
Dabei gibt es verschiedene Möglichkeiten zählend zu richtigen Lösungen zu kommen.
Zählstrategien zur Lösung von Additions- und Subtraktionsaufgaben (am Beispiel der Aufgaben 3+4 und 7-3)
Alleszählen
Beim Alleszählen werden alle beteiligten Mengen abgezählt: zuerst die Ausgangszahl, dann die Veränderung und schließlich das Ergebnis.
Alleszählen bei der Aufgabe 3 + 4
 1. Schritt
1. Schritt
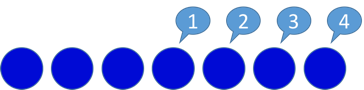 2. Schritt
2. Schritt
 3. Schritt
3. Schritt
Alleszählen bei der Aufgabe 7 - 3
 1. Schritt
1. Schritt
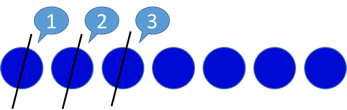 2. Schritt
2. Schritt
 3. Schritt
3. Schritt
Weiterzählen bzw. Rückwärtszählen
Charakteristisch für das Weiterzählen und Rückwärtszählen ist, dass die Ausgangsmenge nicht mehr dargestellt werden muss, sondern nur noch die Veränderung abgezählt wird. Das heißt insbesondere bei der Subtraktion, dass keine Objekte mehr weggenommen werden müssen, sondern dass durch Rückwärtszählen ermittelt wird, wie viele übrigbleiben würden.
Dieses Vorgehen kann sehr fehleranfällig sein – vor allem dann, wenn der Zählprozess vom Kind „versteckt“ wird (für weitere Beispiele vgl. Schulz 2014, S. 98 ff.).
Weiterzählen bei der Aufgabe 3 + 4
 1. Schritt
1. Schritt
 2. Schritt
2. Schritt
 3. April
3. April
Rückwärtszählen bei der Aufgabe 7 - 3 (mit der Vorstellung des Wegnehmens)
 1. Schritt
1. Schritt
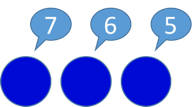 2. Schritt
2. Schritt
 3. Schritt
3. Schritt
Rückwärtszählen bei der Aufgabe 7 - 3 (mit der Vorstellung des Schritte-Gehens)
 1. Schritt
1. Schritt
 2. Schritt
2. Schritt
 3. Schritt
3. Schritt
Zählendes Rechnen im größeren Zahlenraum
Zählende Lösungsfindungen beschränken sich nicht auf einen Zahlenraum, den man gut mit zwei Händen bewältigen könnte (oder einer überschaubaren Anzahl an Material), sondern sie sind auch bei Schülerinnen und Schülern zu beobachten, die Aufgaben im Zahlenraum bis 100 und darüber hinaus lösen müssen.
Da hierbei das Gedächtnis jedoch enorm strapaziert würde, wenn die beteiligten Zahlen als Ganzes abgezählt werden, werden die Zahlen meist in Bestandteile zerlegt, die sich leichter abzählen lassen.
Peters Lösungsweg ist hierbei sehr typisch: Die Zahlen werden in Ziffern zerlegt, da das Rechnen mit Ziffern wieder ein Rechnen im kleinen Zahlenraum ist und gut mit Fingern oder Material (oder im Kopf) bewältigt werden kann (für weitere Beispiele vgl. Schulz 2014, S. 97 ff.).
Auch das Aufsagen von Malreihen als einzige Möglichkeit Multiplikationsaufgaben zu lösen, kann als eine Form des zählenden Rechnens angesehen werden, weil auch hier nicht gerechnet, sondern die Reihe abgezählt werden (vgl. Gaidoschik 2014).
Warum halten manche Kinder so lange am zählenden Rechnen fest?
-
Zählendes Rechnen wird als erfolgreiches Vorgehen wahrgenommen:
Gerade weil das zählende Rechnen zu Beginn des Rechnenlernens eine zielführende Strategie ist, mit der die Kinder häufig zu richtigen Lösungen kommen, wird es von vielen Kindern als sehr erfolgreich wahrgenommen.
-
Zählendes Rechnen wird als Rechnen (miss-)verstanden:
Die erfolgreiche Nutzung von zählender Lösungswege kann irgendwann dazu führen, dass das zählende Lösen von Aufgaben von einigen Kindern mit „Rechnen“ gleichgesetzt wird: Aufgabenlösen ist Zählen ist Rechnen. Diese beiden Sichtweisen (Zählen ist Rechnen und zudem erfolgreich) können sich dann festigen, wenn im Unterricht häufig nur richtige Lösungen verstärkt werden – und der Rechenweg somit in den Hintergrund tritt.
-
Zählendes Rechnen bietet (scheinbare) Sicherheit:
Wenn sich das Zählen als erfolgreiche Methode etabliert, Plus- und Minusaufgaben zu lösen, dann bietet es auch Sicherheit. Andere Möglichkeiten der Lösung werden dann nicht genutzt. Das kennen vielleicht auch wir als Erwachsene – zum Beispiel, wenn es um die Ermittlung von Urlaubstagen über die Monatsgrenze geht (wie viele Übernachtungen muss ich vom 28. August bis zum 4. September buchen...?).
-
Zusammenhänge und Beziehungen werden nicht erkannt:
Das verfestigte zählende Rechnen kann das Erkennen von arithmetischen Zusammenhängen und die Entwicklung von mentalem Werkzeug erschweren, und zwar weil diese beim zählenden Lösen von Aufgaben gar nicht gesehen und genutzt werden müssen.
Diese Gründe deuten auf einen „Teufelskreis“ hin. Einerseits gilt: Wenn ein Kind Aufgaben vor allem zählend löst, kann es schwer geeignetere Strategien und mentales Werkzeug entwickeln und es kann schwer Zusammenhänge zwischen Zahlen und Aufgaben erkennen. Und andererseits: Wenn das Kind noch kein mentales Werkzeug und geeignetere Strategien nutzen kann und noch keine Zusammenhänge zwischen Aufgaben und Zahlen erkennt und nutzt, hält es am zählenden Rechnen fest (für diesen Kasten vgl. Schulz 2014).
Welches sind die Voraussetzungen für die Ablösung vom zählenden Rechnen?
Damit ein Kind (oder ein Erwachsener) nicht auf zählende Lösungsprozesse angewiesen ist, sondern er oder sie stattdessen rechnen kann, ist eine Vielzahl an mentalem Werkzeug notwendig (vgl. z. B. Rathgeb-Schnierer 2011, 2010). Was genau ist mit diesem mentalen Werkzeug gemeint?
Diese Frage soll am Beispiel verschiedener möglicher Lösungsprozesse der Aufgabe 63-28 beantwortet werden.


Auch Sie werden beim Lösen der Aufgabe 63-28 mentales Werkzeug genutzt haben und finden vielleicht in den oben genannten Beispielen „Bestandteile“ Ihres Lösungsweges wieder und können jetzt ein bisschen genauer erkennen, was genau beim Rechnen in Ihrem Kopf vorgegangen ist.
Mit diesen Beispielen kann gut gezeigt werden, dass Rechnen ein mentales Vorgehen ist, bei dem verschiedene Teilaufgaben im Kopf gelöst werden müssen. Diese Teilaufgaben können nur dann bewältigt werden, wenn sogenanntes mentales Werkzeug vorhanden ist.
Bei diesem mentalen Werkzeug handelt es sich unter anderem um ...
-
... auswendig gewusste Aufgaben
-
... das Kennen und Nutzen von Rechengesetzen
-
... ein tragfähiges Operationsverständnis
-
... ein tragfähiges Stellenwertverständnis (im größeren Zahlenraum)
-
... einen Zahlen- bzw. Aufgabenblick.
Erst wenn dieses Werkzeug vom Kind genutzt werden kann, ist eine Ablösung vom zählenden Rechnen möglich.
Daher ist es ein wichtiges Ziel im mathematischen Anfangsunterricht, diese Werkzeug gemeinsam mit den Kindern zu erarbeiten.
Die verschiedenen mentalen Werkzeuge entwickeln sich dabei nicht unabhängig voneinander.
Mentales Werkzeug - ein Glossar
Auswendig gewusste Aufgaben
Die wichtigsten Aufgaben, mit denen alle anderen Aufgaben gelöst werden können, sind die Aufgaben des „kleinen Eins-plus-Eins“. Das sind alle Plus- und Minusaufgaben bis Zehn. Auch die Verdopplungs- und Halbierungsaufgaben bis 20 können gut auswendig gewusst und beim Rechnen genutzt werden.
Rechengesetze und arithmetische Zusammenhänge
Die wichtigsten arithmetischen Zusammenhänge und Rechengesetze für den Mathematikunterricht in der Grundschule sind die folgenden:
-
Das Kommutativgesetz (Tauschaufgaben: z.B. 3+4 = 4+3)
-
Das Assoziativgesetz (Zahlen können „auseinandergenommen und zusammengesetzt“ werden: z. B. 7+8 = 7+3+5 = 10+5 = 15)
-
Addition und Subtraktion sind „Gegenoperationen“ („Wenn ich die Aufgabe 3+4=7 kenne, kenn ich auch die Aufgaben 7-4=3 und 7-3=4“)
-
Konstanz der Differenz („Wenn ich beide Zahlen bei einer Minus-Aufgabe um den gleichen Wert verändere, bleibt das Ergebnis gleich“)
-
Konstanz der Summe („Wenn ich bei der Aufgabe 7+8 von der sieben zwei wegnehme und zu der acht dazutue, dann bleibt das Ergebnis gleich.“)
-
Analogien („13 + 5 kann ich leicht rechnen, weil ich 3+5 weiß und dann noch die zehn dazu“)
Operationsverständnis
Über ein tragfähiges Operationsverständnis verfügt ein Kind dann, wenn es zum Beispiel in der Lage ist, zu einer Rechenaufgabe eine Geschichte zu erzählen oder ein Bild zu malen oder eine Materialhandlung durchzuführen – und umgekehrt (vgl. Operationsverständnis).
Stellenwertverständnis
Bündeln und Entbündeln werden als Grundlage der Schreib- und Sprechweise von Zahlen gekannt und somit auch der Unterschied zwischen Zehnern und Einern (und Hundertern, Tausendern, ...). Das Kind weiß, dass Zahlen (geschrieben, gesprochen und am Material) sich aus Zehnern und Einern (und Hundertern, Tausendern, ...) zusammensetzen. Die Kinder kennen den Zusammenhang zwischen geschriebenen, gesprochenen und am Material dargestellten Zahlen (vgl. Stellenwertverständnis).
Zahlen- und Aufgabenblick
Das Kind erkennt bereits vor oder während des Rechnens einer Aufgabe, wie es die Aufgabe am besten lösen könnte. Hierbei geht es vor allem um das Erkennen von Zahlbeziehungen unter intuitiver Nutzung der anderen oben beschriebenen mentalen Werkzeuge („Die Aufgabe 7+9 kann ich einfach lösen, weil neun in der Nähe von 10 liegt, und 7+10 weiß ich auswendig, und dann muss ich wieder einen wegnehmen, weil ich einen zuviel gerechnet habe.“).
Auf der Unterseite Unterricht finden Sie Antworten auf die Frage:
-
Wie kann ich die Schülerinnen und Schüler im Unterricht bei der Entwicklung des mentalen Werkzeugs unterstützen?
Diese Seite wurde erstellt von Axel Schulz für das primakom-Team.