Einstieg

Kannst du das auch anders rechnen?!

In einer 3.  Klasse wurde nach der Auseinandersetzung mit unterschiedlichen halbschriftlichen Strategien der Subtraktion vor einigen Wochen der schriftliche Subtraktionsalgorithmus eingeführt. Marleen darf die folgende Aufgabe auf eigenen Wegen lösen - ihre Lehrerin tritt dabei mit ihr über ihren Lösungsprozess ins Gespräch:

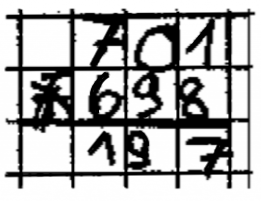
Wie viel ist 701-698?
8 minus 1 gleich 7, 9 minus 0 gleich 9, 7 minus 6 gleich 197!

Kannst du das auch anders rechnen?
Ja. Von 698 bis 700 sind es 2 und von 701 bis 700 ist es 1, also sind´s 3.

Mhm. Die selbe Aufgabe, aber zwei verschiedene Ergebnisse?
Mhm, weiß auch nicht.

Kann denn Beides richtig sein?
Ne.

Was denkst du denn, was stimmt?
Das da! (Sie zeigt auf das schriftlich Gerechnete.)

Warum glaubst du, dass das stimmt und das andere nicht?
Ja, weil das hier (zeigt auf das schriftlich Gerechnete) habe ich richtig ausgerechnet und das andere habe ich mit nur so hopp-di-hopp im Kopf überlegt.

Das Gespräch zeigt, welches Vertrauen Marleen in den schriftlichen Algorithmus und somit in das durch diesen Verfahren gefundene Ergebnis legt. Ihre (viel tiefergehenden?!) Überlegungen, die sie für den alternativen Rechenweg im Kopf aufzeigt, verwirft sie bzw. stellt sie in diesem Augenblick unter das gewählte Lösungsverfahren.
 
Aus der Antwort auf die Frage „Kannst du das auch anders rechnen?“ wird deutlich, dass Marleen jedoch „genau hingeschaut“ hat und die Besonderheit der Aufgabe bzw. die Beziehung zwischen den beiden Zahlen (dass sie nah beieinanderliegen, und durch „Ergänzen“ schnell eine Lösung gefunden werden kann) erkannt hat und auch zu einer alternativen Ergebnisfindung nutzen konnte.
 
An dieser Stelle wollen wir uns nicht fragen, warum sie dennoch bei dem schriftlichen Algorithmus bleibt und diesem vertraut, sondern viel eher, wie es gelingen könnte, dass sie die Zahlen- und Aufgabenmerkmal der Aufgabe nutzt, um hier das Kopfrechnen als den geeigneteren Rechenweg wahrzunehmen und somit flexibler rechnet?