Halbschriftliche Rechenstrategien
Wenn Sie die Inhalte Ihrer Mathematikbücher vom ersten bis zum vierten Schuljahr betrachten, stellen Sie fest, dass die halbschriftlichen Rechenstrategien unabhängig vom Lehrwerk ab der zweiten Klasse eine zentrale Bedeutung im Unterricht haben und über die gesamte Grundschulzeit hinweg einen großen Raum einnehmen. Dabei werden nicht etwa eine oder zwei Strategien thematisiert, sondern verschiedene.

Es stellt sich die Frage, warum diese Rechenstrategien eine solche zentrale Rolle einnehmen und nicht etwa, wie es Herr Vogel in dem Einstiegsbeispiel fordert, sehr früh das schriftliche Rechnen thematisiert wird. Der nachfolgende Arbeitsauftrag soll dazu einen ersten Einblick geben.
Damit Sie darauf aufbauend gut auf den Unterricht vorbereitet sind, nehmen wir anschließend Folgendes in den Blick:
Zurück zur Ausgangsfrage: Warum sind halbschriftliche Strategien wichtig? Lösen Sie dazu die kommende Aufgabe und reflektieren Sie:
Eigenaktivität
Wie lösen Sie die folgenden Aufgaben?

Vermutlich wählen Sie nicht immer das gleich Vorgehen. Warum nicht?
Welche Besonderheiten gibt es bei halbschriftlichen Rechenstrategien?
Das zentrale Kennzeichen des halbschriftlichen Rechnens ist also das Zerlegen von Aufgaben in leichtere Teilaufgaben. Einzelne Rechenschritte werden notiert, bis am Schluss das Ergebnis ermittelt ist (vgl. Selter 1999, S. 6). Unabhängig von der Rechenoperation (Addition, Subtraktion, Multiplikation und Division) sind die halbschriftlichen Strategien durch drei besondere Charakteristika gekennzeichnet. Für die Thematisierung der halbschriftlichen Strategien ist es zentral diese zu kennen. Sie werden nachfolgend erläutert.
Konkrete Videos, in denen die Besonderheiten anhand von Schülervorgehensweisen erläutert werden, finden Sie auf der Seite des Projektes KIRA.
1. Die Rechenwege sind beim halbschriftlichen Rechnen, anders als beim schriftlichen Rechnen, nicht vorgegeben.
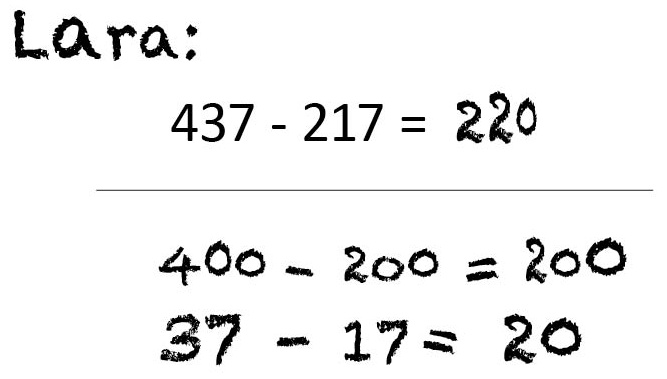

Erläuterung:
In den Schülerlösungen sieht man, dass Lara und Linus zwei sehr unterschiedliche Zerlegungen der Zahlen nutzen, um das Ergebnis zu ermitteln (eine Übersicht zu häufig genutzten Strategien finden Sie im nachfolgenden Abschnitt).
2. Die Notationsweise ist nicht verbindlich festgelegt.
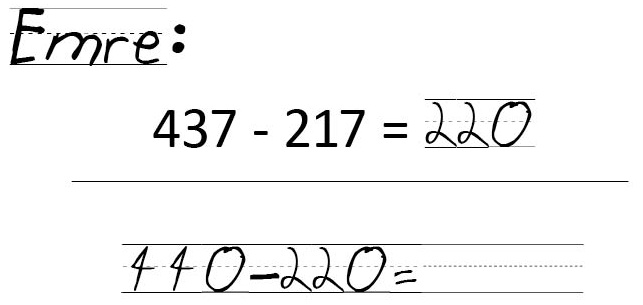
Erläuterung:
Die Kinder notieren, wie bei Emres Vorgehen zu sehen, nicht unbedingt alle Teilschritte. Das Notieren der Schritte dient lediglich als Merkhilfe. Welche Schritte die Kinder notieren, bleibt ihnen selbst überlassen.
3. Es gibt verschiedene halbschriftliche Lösungsstrategien und es hängt von der jeweiligen Aufgabe ab, welche Lösungsstrategie besonders sinnvoll ist.

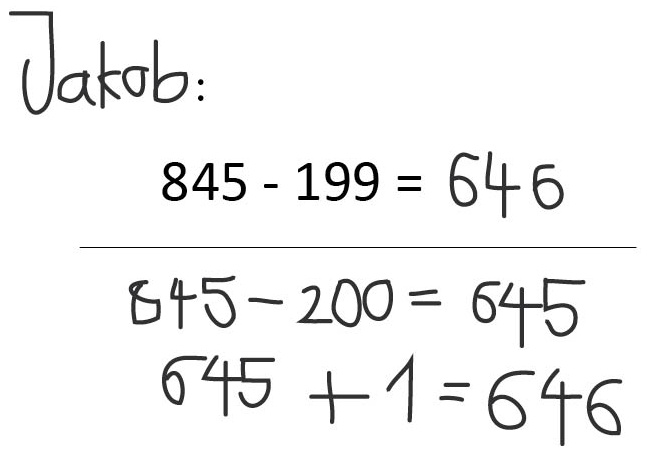
Erläuterung:
Erinnern Sie sich noch einmal an Ihre Strategien zur Lösung der eingangs gestellten Aufgaben "437 - 217" und "845 - 199" zurück. Sie haben vermutlich nicht bei beiden Aufgaben das gleiche Vorgehen verwendet, richtig?
Warum eigentlich nicht?
Wahrscheinlich weil für Sie auf der Hand lag, dass es einfacher ist, die erste Aufgabe mit einer anderen Strategie zu lösen als die zweite. So bietet es sich an, bei der ersten Aufgabe Hunderter, Zehner und Einer zu subtrahieren.
Dieses Vorgehen ist bei der Aufgabe 845 - 199 wenig sinnvoll.
Grundsätzlich gibt es demnach Strategien, die sich bei einer Aufgabe besonders anbieten und andere weniger. Dennoch gibt es nicht zwangsläufig zu einer Aufgabe eine beste Strategie, sondern oftmals mehrere sinnvolle Wege.
Was bedeuten diese Charakteristika für Ihren Unterricht?
Wenn die Rechenwege nicht vorgegeben sind, die Notationsweise frei wählbar ist und es verschiedene sinnvolle Strategien gibt, kann das Unterrichtsziel nicht darin bestehen, ein fest vorgeschriebenes Verfahren einer halbschriftlichen Strategie, "die immer zum richtigen Ergebnis führt", zu erlernen.
Das Ziel des Unterrichts ist es vielmehr, zu verstehen, warum und wie die verschiedenen Rechenstrategien funktionieren. Außerdem ist es wesentlich, sich bewusst zu werden, bei welchen Aufgaben welche Strategien besonders effektiv sind. Diese Ziele werden entsprechend auch in den Bildungsstandards festgehalten: Die Kinder sollen bis zum Ende der vierten Jahrgangsstufe „mündliche und halbschriftliche Rechenstrategien verstehen und bei geeigneten Aufgaben anwenden, verschiedene Rechenwege vergleichen und bewerten; Rechenfehler finden, erklären und korrigieren" (KMK 2004, S. 9).
Welche halbschriftlichen Strategien gibt es?
Obwohl die Rechenwege nicht verbindlich vorgegeben sind, gibt es zu jeder Rechenoperation eine insgesamt überschaubare Anzahl von Hauptstrategien. Für Ihren Unterricht ist es von zentraler Bedeutung, diese Strategien zu kennen. Nachfolgend werden exemplarisch die Strategien zur halbschriftlichen Subtraktion im Tausenderraum dargestellt.
Die Haupstrategien zu den anderen Rechenoperationen werden übersichtlich auf der Webseite des Projektes KIRA aufgeführt und an Beispielen erläutert. Hier gelangen Sie direkt zur Addition, Multiplikation und Division:
KIRA: Arithmetik – Halbschriftliches Rechnen – Addition
KIRA: Arithmetik – Halbschriftliches Rechnen – Multiplikation
KIRA: Arithmetik – Halbschriftliches Rechnen – Division
Strategien am Beispiel Tausenderraum
1. Schrittweise
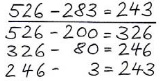
Erklärung der Strategie und Hinweise zum sinnvollen Einsatz
2. Stellenweise
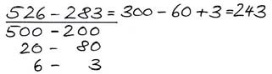
Erklärung der Strategie und Hinweise zum sinnvollen Einsatz
3. Stellenweise mit Wechseln/Eintauschen
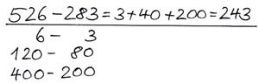
Erklärung der Strategie und Hinweise zum sinnvollen Einsatz
4. Mischformen aus Stellen- und Schrittweise
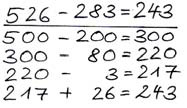
Erklärung der Strategie und Hinweise zum sinnvollen Einsatz
5. Hilfsaufgabe
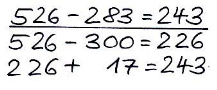
Erklärung der Strategie und Hinweise zum sinnvollen Einsatz
6. Vereinfachen
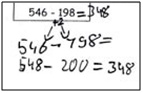
Erklärung der Strategie und Hinweise zum sinnvollen Einsatz
Halbschriftliche Rechenstrategien - Beispiele entnommen aus dem Projekt PIK AS
PIKAS: Fortbildungsmodul: Lernen auf eigenen Wegen – Addieren und Subtrahieren auf eigenen Wegen
In der aus dem Unterrichtsmaterial des Projektes PIK AS übernommenen Tabelle sind die verschiedenen Strategien immer subtraktiv gedacht. Für Ihren Unterricht gilt es zu berücksichtigen, dass man die Subtraktionsaufgaben ebenso additiv lösen kann. Wenn Sie die Aufgabe 526 - 283 additiv lösen, ist die zentrale Frage: Wie viel muss ich zu 283 hinzufügen, damit ich 526 erhalte?
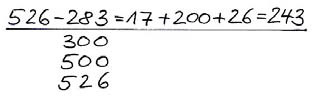 (additives stellenweises) Ergänzen
(additives stellenweises) Ergänzen
Ein solches additives Vorgehen sollte im Unterricht unbedingt ebenfalls zugelassen und auch thematisiert werden. Weitere Informationen zu dieser Sichtweise auf Subtraktionsaufgaben sind auf der Seite Operationsverständnis aufbauen gespeichert.
Was bedeutet dies für Ihren Unterricht?
Da es nicht die beste Strategie gibt, sondern die Kinder gemäß der KMK (2004) vielmehr lernen sollten, Strategien in Abhängigkeit von den gegebenen Zahlenwerten und den eigenen Präferenzen einzusetzen, ist es wesentlich, dass Sie in ihrem Unterricht gemeinsam mit den Kindern darüber reflektieren, welche Rechenstrategien sich bei einem bestimmten Aufgabentypen besonders anbieten und welche für diesen Aufgabentyp eventuell weniger geeignet sind.
Damit lernen die Kinder, wie beispielsweise im Lehrplan des Landes NRW bis zum Ende der Klasse 4 gefordert, unterschiedliche Rechenwege unter dem Aspekt des vorteilhaften Rechnens zu beschreiben und zu bewerten (→ Stichwort flexibles Rechnen) (vgl. MSW NRW 2008, S. 62).
Die Thematisierung der halbschriftlichen Strategien ist übrigens nicht nur wesentlich, um Kopfrechenstrategien in größeren Zahlenräumen zu entwickeln. Sie ist zugleich die Vorbereitung auf das schriftliche Rechnen. So kann aus dem "Stellenweise mit Wechseln/Eintauschen" das Entbündelungsverfahren abgeleitet werden und aus dem "(additiven stellenweisen) Ergänzen" das Auffüllen. Genauere Informationen dazu finden Sie auf der Seite Schriftliche Rechenverfahren.
Wie kann man Rechenstrategien veranschaulichen?
Vielleicht haben Sie die Aufgabe 845 - 199 auch intuitiv über die Hilfsaufgabe 845 - 200 gelöst, indem Sie zum Ergebnis 645 noch 1 addiert haben? Oder durch Vereinfachen, also 846 - 200? Aber warum ist dies eigentlich möglich? Kinder sollten im Unterricht nicht nur lernen Rechenstrategien anwenden zu können, sondern insbesondere auch verstehen, warum und wie sie funktionieren. Für Ihren Unterricht sind daher Veranschaulichungen am Material von zentraler Bedeutung.
Aber: Wie kann man einem Kind veranschaulichen, wie z. B. dass 845 - 199 das Gleiche wie 846 - 200 ist? Wie können die Kinder die anderen Strategien verstehen? Grundsätzlich eignen sich zur Veranschaulichung Mehrsystemblöcke (Hunderterplatten, Zehnerstangen und Einerwürfel) und der Rechenstrich besonders gut. Die beiden nachfolgenden PIK AS Videos geben exemplarisch Einblicke, wie mit Hilfe dieser Materialien die Strategien "Stellenweise mit Wechseln/Eintauschen" und "Ergänzen" veranschaulicht werden können.
"Stellenweise mit Wechseln/Eintauschen"
(Unterrichtsszene aus dem Projekt Pikas)
"Ergänzen"
(Unterrichtsszene aus dem Projekt PIKAS)
Die Videos zeigen exemplarisch eine Veranschaulichung zweier halbschriftlicher Strategien. Die Unterrichtsszenen sind dabei in einem anderen Kontext entstanden: Ziel der Unterrichtsstunden war jeweils die Einführung der schriftlichen Subtraktion. Dabei wurde auf die bereite bekannten Strategien zurückgegriffen.
In den meisten Schulbüchern erhalten Sie Hinweise, wie Sie auch die weiteren Strategien durch Materialhandlungen veranschaulichten können.
Welche typischen Fehler machen Lernende?
Vielleicht ist Ihnen in Ihrem Unterricht aufgefallen, dass einige Fehler von Kindern besonders häufig gemacht werden. Man spricht daher auch von typischen Fehlern. Macht ein Kind regelmäßig den gleichen Fehler, so weist dies oftmals auf ein Fehlkonzept des Lernenden hin. Zentral ist es, in diesen Fällen die fehlerhaften aber dennoch plausiblen Denkwege der Kinder zu verstehen und den Kindern bewusst zu machen. Bei der halbschriftlichen Subtraktion tauchen relativ häufig die drei folgenden Fehler auf (vgl. Meseth & Selter 2001):
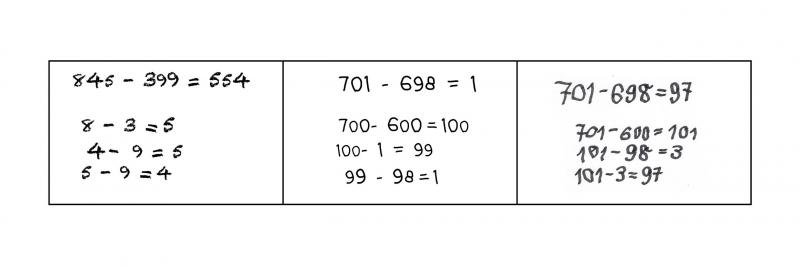
Eigenaktivität
Können Sie die Fehler erklären?
Überlegen Sie auch welche sinnvolle Überlegung der Vorgehensweise zugrunde liegen könnte.
Wie können Sie im Unterricht mit diesen Fehlern umgehen?
Bemerken Sie, dass ein Kind einen Fehler bei verschiedenen Aufgaben immer wieder macht, so ist dieser scheinbar systematisch. Zentral ist es, an dieser Stelle die Aufgaben erneut über Materialhandlungen (s. o.) zu lösen, damit den Kindern der jeweilige Fehler bewusst wird und sich nicht verfestigt.
Zusammenfassung
Kommen wir noch einmal zu unserem Einstiegsbeispiel und den aufgeworfenen Fragen zurück:
-
Warum rechnet man nicht gleich untereinander, also schriftlich, wie Herr Vogel es vorschlägt?
-
Und warum werden in den Schulbüchern verschiedene Rechenwege thematisiert?
-
Reicht es nicht einen Weg zu kennen?
Es lässt sich festhalten, dass halbschriftliche Rechenstrategien aus drei Gründen von zentraler Bedeutung sind:
-
Sie sind neben dem Kopfrechnen, dem schriftlichen Rechnen und dem Taschenrechner ein sinnvoller und oftmals sehr ökonomischer Weg, um Aufgabenstellungen zu lösen.
-
Sie bereiten Kopfrechenstrategien in größeren Zahlenräumen vor.
-
Sie sind die Grundlage, um die schriftlichen Strategien zu verstehen. Dieses Verständnis ist wesentlich, um die schriftlichen Algorithmen richtig ausführen zu können.
Um ein solches Verständnis bei Eltern anzuregen, kann es hilfreich sein, diese auf einem Elternabend aufzufordern, verschiedene Aufgaben zu rechnen und über das eigene Vorgehen zu reflektieren; ähnlich, wie es zu Beginn dieser Seite angeregt wurde.
Abhängig von den jeweiligen Aufgabenstellungen sind verschiedene halbschriftliche Strategien besonders geeignet bzw. weniger geeignet um die jeweiligen Aufgaben zu lösen. Wesentlich ist daher, dass das Ziel bei der Thematisierung halbschriftlicher Strategien nicht darin bestehen darf, ein oder zwei Strategien nach einem starren Schema auf alle Aufgaben anwenden zu können. Es geht vielmehr darum, verschiedene halbschriftliche Strategien zu verstehen und diese in Abhängigkeit von den eigenen Präferenzen und den jeweiligen Aufgabenstellungen flexibel einsetzen zu können. Dabei muss jedoch nicht zwangsläufig jedes Kind auch jede Strategie beherrschen.
Damit kommen wir zur letzten eingangs gestellten Frage: Wie kann man Lernende dabei unterstützen verschiedene Strategien kennenzulernen und flexibel einzusetzen?
Um die Strategien zu verstehen ist dabei der Einsatz von Material notwendig. Besonders geeignet sind Mehrsystemblöcke und der leere Rechenstrich. Zu dem aufgabenadäquaten Einsatz der Strategien bedarf es einer gemeinsamen unterrichtlichen Reflexion. Wie dies ganz konkret umgesetzt wird, erfahren Sie im Unterrichtsteil.