Unterricht

Welche zentralen Ziele sollten bei der Thematisierung halbschriftlicher Rechenstrategien verfolgt werden und wie sieht eine konkrete Unterrichtsreihe aus?

Nachfolgend werden diese Fragen exemplarisch für die Subtraktion im Tausenderraum beantwortet. Die dargestellten Ziele und Ausführungen basieren dabei auf einer im Rahmen des Projektes PIK AS entwickelten und erprobten Unterrichtsreihe. Die vollständigen Unterrichtsmaterialien finden Sie im Materialteil.

Sollten Sie halbschriftliche Strategien in einem anderen Zahlenraum (Hunderterraum in Klasse 2) oder zu anderen Rechenoperationen (Addition, Multiplikation und Division) thematisieren, so ist es möglich, die Ziele und Überlegungen analog auf diese zu übertragen. Wichtig ist dabei, dass Sie sich im Vorfeld mit den jeweiligen spezifischen Strategien, Materialdarstellungen sowie den Schwierigkeiten und Fehlern der Kinder auseinandersetzen.

Ziele des Unterrichts

Zahlen und Operationen

Die Kinder können

• "mündliche und halbschriftliche Rechenstrategien verstehen und bei geeigenten Aufgaben anwenden",
• "verschiedene Rechenwege vergleichen und bewerten; Rechenfehler vergleichen und bewerten; Rechenfehler finden, erklären und korrigieren",
• "Rechengesetze erkennen, erklären und benutzen" (KMK 2004, S. 9).

Problemlösen/kreativ sein

Die Kinder können "Lösungsstrategien entwickeln und nutzen (z.B. systematisch probieren)" (KMK 2004, S. 7).

Kommunizieren

Die Kinder können "eigene Vorgehensweisen beschreiben, Lösungswege anderer verstehen und gemeinsam darüber reflektieren" (KMK 2004, S. 8).

Argumentieren

Die Kinder können "Begründungen suchen und nachvollziehen" (KMK 2004, S. 8).

Strukturierung des Unterrichts

Die nachstehend skizzierte Unterrichtsreihe aus dem Projekt PIK AS zeigt beispielhaft auf, wie Kinder im dritten Schuljahr Strategien zur halbschriftlichen Subtraktion im Tausenderraum entwickeln können. Sie ist dabei im Sinne des Ich-Du-Wir-Prinzips strukturiert.
Grob dargelegt bedeutet dies, dass die Kinder zunächst auf eigenen, informellen Wegen Strategien entwickeln (1. Ich-Phase), um sich diese dann in Kooperation und Kommunikation mit anderen Kindern gegenseitig vorzustellen (2. Du-Phase) und schließlich weniger fehleranfällige und zeitaufwändige Strategien zu favorisieren und Kenntnisse von und Kompetenzen im Umgang mit "regulären" Rechenwegen zu erwerben (3. Wir-Phase).

Hinweise zum Material

Zentrale "Forschermittel", also Anschauungs- und Darstellungsmittel, sind für die nachfolgende Unterrichtsreihe auf der Handlungsebene die Zehner-System-Blöcke ("Dienes-Material") sowie auf der ikonische Ebene die Strich-Punkt-Darstellung ("Oehl’sche Darstellung") und der Rechenstrich ("leere Zahlenstrahl").

Die für die Unterrichtseinheit ausgewählten Subtraktionsaufgaben sind so gewählt worden, dass sie 'hineingedachte Lösungsstrategien' implizieren. Hierzu finden Sie Übersichten (zur Addition und Subtraktion), die illustrieren, welche Strategie bei welcher Aufgabe als "geschickt" einzuschätzen ist.

Lernvoraussetzungen

Das Unterrichtsvorhaben für das dritte Schuljahr kann durchgeführt werden, wenn

• sich die Kinder im Zahlenraum bis 1000 sicher orientieren;
• sie die notwendigen Anschauungsmittel zur Zahl- und Operationsdarstellung (Rechenstrich, Zehner-System-Blöcke...) sachgerecht nutzen können.

Grundsätzlich ist es sinnvoll, die Unterrichtsreihe vorab bereits im zweiten Schuljahr - nach den Orientierungsübungen im Hunderterraum - mit angepasstem Zahlenmaterial analog durchzuführen.

Unterrichtsreihe

1. Einheit: Vorkenntnisse der Kinder erheben

Ziele

• Erheben und Nutzen der Vorkenntnisse der Kinder zur Planung der gezielten Förderung.
• Schaffung von Transparenz über das neue Thema für die Kinder. Kinder können ggf. lernen einzuschätzen, was sie bereits können und was sie noch lernen müssen.

Zeit

1 Schulstunde

Darum geht es: 

Die Kinder erhalten im Rahmen der Standortbestimmung Subtraktionsaufgaben im Hunderter- und Tausenderraum, die sich mit analogen halbschriftlichen Strategien lösen lassen. Durch die Gegenüberstellung von Subtraktionsaufgaben aus dem bekannten Hunderterraum als Grundanforderung gegenüber solchen aus dem neuen Tausenderraum wird das Erkennen und Nutzen von Analogien angeregt.

Bei der Auswertung der Standortbestimmungen sollte auf folgende Aspekte fokussiert werden:

• Welche Kompetenzen bringen die Kinder aus dem zweiten Schuljahr mit? Welche Kenntnisse über die verschiedenen halbschriftlichen Strategien haben sie?
• Sind sie dazu in der Lage, diese Kompetenzen anzuwenden und auf den neuen Zahlenraum zu übertragen? Werden die Analogien erkannt und genutzt?
• Welche Strategien wählen sie? Wählen sie verschiedene Strategien oder stets die gleiche? Sind die gewählten Strategien - aus der Sicht des geübten Rechners - "geschickt", also haben die Kinder bereits einen "Zahlen und -Aufgabenblick", oder eher nicht?

Mögliche Knackpunkte

• Je nachdem wie die Thematisierung in der zweiten Klasse erfolgte, ist es möglich, dass die Kinder vorrangig die Strategien "Stellenweise" und "Schrittweise" verwenden. Für die nachfolgenden Unterrichtsstunden ist es dann wesentlich, weitere Strategien anzubahnen.
• Ggf. ermitteln Kinder bei Subtraktionsaufgaben mit Übertrag immer fehlerhafte Ergebnisse, weil sie die Strategie "Stellenweise" direkt von der Addition auf die Subtraktion übertragen (vgl. Hintergrund "typische Fehler")

2. Einheit: Eigene Rechenstrategien entwickeln

Ziele

• Initiierung eigener Lösungswege unter Nutzung von "Forschermitteln" (Zehner-System-Blöcke, Rechenstrich...).
• Austausch über verschiedene Rechenwege in Mathe-Konferenzen (vgl. Haus 8, UM: Plakate, IM: Infopapier, Video).

Zeit

3 - 4 Schulstunden

Darum geht es

Die Kinder erhalten zunächst den Auftrag verschiedene Subtraktionsaufgaben selbstständig unter Verwendung von Forschermitteln zu lösen und darüber zu reflektieren, ob sich ein Rechenweg besonders anbietet.

In den anschließenden Mathekonferenzen tauschen die Kinder die verschiedenen gefundenen Lösungswege aus.

Mögliche Knackpunkte

• Materialeinsatz: Sollten die Anschauungsmaterialien den Kindern nicht bekannt sein, so ist es wesentlich zu thematisieren, wie man mit Hilfe der Materialien die Subtraktionsaufgaben lösen kann - (Zur Veranschaulichung der Strategien mit Forschermitteln können Sie sich über den Link weiterinformieren).
• Methodenkenntnis: Wenn Mathekonferenzen nicht bekannt sind, können die Kinder alternativ ihre gefundenen Lösungswege im Plenum präsentieren.

3. Einheit: "Rechne wie..."

Ziele

• Sensibilisierung der Kinder für die Vielfalt möglicher Rechenwege: "Dass es viele Rechenwege gibt, die man an einer einzigen Aufgabe anwenden kann".
• Es geht nicht darum, dass alle Kinder sämtliche Strategien geläufig beherrschen sollen.

Zeit

3 - 4 Schulstunden

Darum geht es

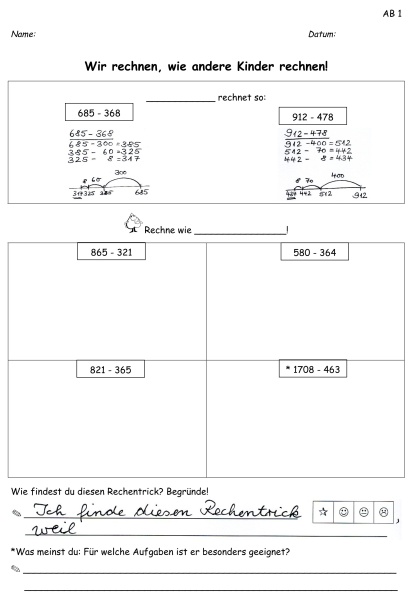
Die Kinder vollziehen zunächst die verschiedenen "schlauen" Strategien (anderer Kinder) aktiv nach und sind anschließend aufgefordert, diese zu bewerten und zu überlegen, bei welchen Zahlenwerten sie diese anwenden würden. Im Anschluss erhalten sie den Auftrag, wie das jeweilige Kind zu rechnen.

Sie wählen vorab aus den Ergebnissen der 2. Einheit zu allen Strategien Schülerlösungen aus. Sind nicht alle Strategien verwendet worden, so ergänzen Sie diese.

Am Ende dieser Einheit sollten alle Kinder die Strategie "Stellenweise" verstanden haben, da diese die Grundlage zur Thematisierung der schriftlichen Strategien ist.

Mögliche Knackpunkte

Wesentlich ist, dass die Kinder die Strategien der anderen nachvollziehen können. Zur Erklärung und bei der eigenen Anwendung der Strategien ist es evtl. sinnvoll, dass die Kinder wieder auf Materialdarstellungen zurückgreifen.
In dieser Phase des Lernprozesses ist neben dem Verständnis insbesondere die Reflektion über die Eignung der Strategien zentral.

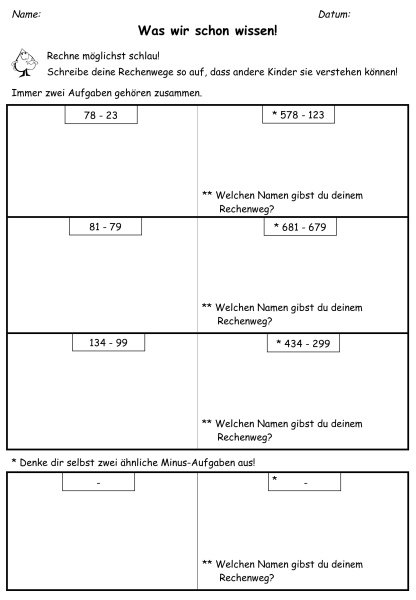
4. Einheit: "Rechne möglichst schlau!"

Ziele

Selbstständige Einordnung und Bewertung eigener und fremder Strategien hinsichtlich ihrer Effizienz.

Zeit

1 - 2 Schulstunden

Darum geht es

Die Kinder erhalten Aufgabenstellungen, die durch die unterschiedlichen Zahlenwerte jeweils eine Rechenstrategie besonders nahelegen.
Sie sollen begründet entscheiden, welche Strategie(n) sich bei welcher Aufgabe gut eignen.

5. Einheit: Erheben des Lernzuwachses der Kinder

Ziele

Erhebung individueller Lernzuwächse sowie ggf. die Ableitung weiterer Fördermaßnahmen.

Zeit

1 - 3 Schulstunden, abhängig von der Ausführlichkeit der Rückmeldung

Darum geht es

Die Kinder erhalten durch den systematischen Vergleich der Eingangs- und Abschlusstandortbestimmungen Einblicke in den eigenen Lernzuwachs.