Warum lernen Kinder schriftliche Rechenverfahren?
Für das schriftliche Rechnen ist, neben dem ziffernweisen Rechnen, der Einsatz eines Algorithmus charakteristisch. Unter einem Algorithmus versteht man eine „endliche Abfolge von eindeutig bestimmten Elementaranweisungen, die den Lösungsweg eines Problems exakt und vollständig beschreiben" (Ziegenbalg 1996, S. 23) und die schrittweise garantiert zu einer richtigen Lösung führen.
Algorithmen bilden einen wichtigen Bestandteil der Mathematik. Wir finden sie in vielen Bereichen. Auf dieser Seite beschränken wir uns aber auf die schriftlichen Rechenverfahren und gehen dabei auf die folgenden Punkte ein:
Schriftliche Rechenverfahren: Was verstehen wir darunter?
Das zentrale Kennzeichen des schriftlichen Rechnens ist das Zerlegen der Zahlen in Ziffern, die bei der Addition und Subtraktion stellengerecht untereinander geordnet und berechnet werden. Dabei rechnet man nach festen Regeln mit Hilfe eines Algorithmus.
Warum sind die schriftlichen Rechenverfahren wichtig?
Es gibt unterschiedliche Meinungen über die schriftlichen Rechenverfahren.
Einige Gegner des schriftlichen Rechnens argumentieren, dass Taschenrechner (bzw. Endgeräte mit Taschenrechnerfunktion) heutzutage dem schriftlichen Rechnen die Bedeutung nehmen und eine Einführung in der Grundschule überflüssig machen. Taschenrechner seien überall griffbereit und entlasten das Gedächtnis.
Dennoch kann man argumentieren, dass Kinder auch im Alltag mit der "Untereinander-Schreibweise" konfrontiert werden, wie z. B. auf Kassenzetteln oder Rechnungen. Zudem kann der Wechsel von Stift zu Taschenrechner bei komplexeren Aufgaben aufwendiger sein, besonders wenn einige Aufgaben im Kopf leicht lösbar sind und man lediglich Schritte notieren müsste.
Eigenaktivität
Überlegen Sie sich weitere Pro- und Kontra-Argumente die für bzw. gegen die Einführung der schriftlichen Rechenverfahren sprechen.
Wie äußert sich der Rahmenlehrplan zu den schriftlichen Rechenverfahren?
Mit den schriftlichen Rechenverfahren lernen die Kinder das erste Mal einen effektiven mathematischen Algorithmus kennen.
Bezug zum Lehrplan Mathematik Nordrhein-Westfalen (2008)
Die Kinder sollen die schriftlichen Rechenverfahren auf „der Grundlage tragfähiger Zahl- und Operationsvorstellungen sowie verlässlicher Kenntnisse und Fertigkeiten (...) verständig" (MSW NRW 2008, S. 58) ausführen können.
Kompetenzerwartungen am Ende der Klasse 4
Zahlen und Operationen – Ziffernrechnen
„Die Schülerinnen und Schüler erläutern die schriftlichen Rechenverfahren der Addition [und] der Subtraktion (...), indem sie die einzelnen Rechenschritte an Beispielen in nachvollziehbarer Weise beschreiben" (MSW NRW 2008, S. 62).
Problemlösen/Kreativ sein
„Die Schülerinnen und Schüler entnehmen Problemstellungen die für die Lösung relevanten Informationen" (erschließen), „nutzen die Einsicht in Zusammenhänge zur Problemlösung" (lösen) und „übertragen Vorgehensweisen auf ähnliche Sachverhalte" (übertragen) (MSW NRW 2008, S. 59).
Argumentieren
„Die Schülerinnen und Schüler stellen Vermutungen über mathematische Zusammenhänge oder Auffälligkeiten an" (vermuten), „testen Vermutungen anhand von Beispielen und hinterfragen, ob ihre Vermutungen (...) zutreffend sind" (überprüfen) und „erklären Beziehungen und Gesetzmäßigkeiten an Beispielen" (begründen) (MSW NRW 2008, S. 60).
Darstellen/Kommunizieren
„Die Schülerinnen und Schüler bearbeiten komplexere Problemstellungen gemeinsam" (kooperieren und kommunizieren) (MSW NRW 2008, S. 60).
Welche Verfahren gibt es bei der schriftlichen Subtraktion?
Möglicherweise haben Sie sich schon einmal gefragt, warum in verschiedenen Schulbüchern manchmal "anders" schriftlich gerechnet wird. Im Folgenden zeigen wir exemplarisch am Beispiel der schriftlichen Subtraktion, welche Verfahren es zu unterscheiden gilt. Unter dem Menüpunkt
Material finden Sie dann Hinweise, für die übrigen Rechenoperationen.
Prinzipiell unterscheidet man zwischen Verfahren, bei denen die Differenz durch Abziehen bestimmt wird (z. B. 4 - 3 = 1) und solchen, bei denen die Differenz durch Ergänzen bestimmt wird (von 1 bis 4 sind es 3, also 1 + 3 = 4). Des Weiteren werden die Subtraktionsverfahren durch die Art des Übertrags bestimmt. Hier gibt es die Möglichkeiten zu entbündeln, zu erweitern und aufzufüllen. Nun kann man das Ergänzen und Abziehen mit den verschiedenen Übertragstechniken kombinieren und erhält somit fünf Verfahren der schriftlichen Subtraktion (vgl. Padberg & Benz 2011, S. 239ff.).
Entbündeln
Bei diesem Verfahren wird lediglich der Minuend umgeformt, indem zum Rechnen ein größerer Stellenwert aufgelöst und somit für den nächst kleineren Stellenwert entbündelt wird.
Erweitern
Bei diesem Verfahren werden sowohl Minuend als auch Subtrahend um dieselbe Zahl erweitert (z. B. zehn Einer im Minuend und ein Zehner im Subtrahend). Die Differenz verändert sich durch dieses Vorgehen nicht. Somit liegt diesem Verfahren das Gesetz von der Konstanz der Summe zugrunde.
Auffüllen
Bei diesem Verfahren wird der Subtrahend stellenweise (beginnend bei den Einern) so lange aufgefüllt, bis man den Wert des Minuenden erreicht hat.
Abziehen (Minus-Sprechweise)
Entbündeln
3E - 8E geht nicht. Ich entbündle einen Zehner, sind zehn Einer. So wird aus einem Zehner im Minuenden zehn Einer und ich kann weiterrechnen. Also 13E - 8E = 5E usw.
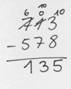
Erweitern
3E - 8E geht nicht. Ich erweitere oben im Minuenden mit zehn Einern und unten im Subtrahenden mit einem Zehner. Damit bleibt die Differenz unverändert (konstant). Durch diese Veränderung kann ich weiterrechnen. Also 13E - 8E = 5E usw.
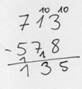
Auffüllen
Kann nicht kombiniert werden.
Ergänzen (Plus-Sprechweise)
Entbündeln
8 + ? = 3 geht nicht. Ich entbündle einen Zehner, sind zehn Einer. So wird aus einem Zehner im Minuenden zehn Einer, und ich kann weiterrechnen. Also 8 + 5 = 13 usw.
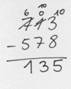
Erweitern
8 + ? = 3 geht nicht. Ich erweitere oben im Minuenden mit zehn Einern und unten im Subtrahenden mit einem Zehner. Damit bleibt die Differenz unverändert (konstant). Durch diese Veränderung kann ich weiterrechnen. Also 8 + 5 = 13 usw.
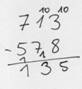
Auffüllen
Auffüllen aber 13 Einer, die ich wiederum zu einem Zehner und 3 Einern bündeln kann.
Die 8 Einer im Subtrahenden fülle ich solange auf, bis ich 13 Einer erhalte. Dazu muss ich 5 Einer hinzufügen. Jetzt sind in der Einerspalte durch mein Den einen Zehner übertrage ich in die Zehnerspalte des Subtrahenden. Jetzt sind im Zehner des Subtrahenden bereits 8 Zehner, die wiederum mit 3 Zehner aufgefüllt werden, so dass 11 Zehner entstehen. Erneut kann ich umbündeln und einen Hunderter übertragen. Zum Schluss muss ich noch die 6 Hunderter auf 7 Hunderter auffüllen.
Eigenaktivität
-
Lösen Sie die folgenden Aufgaben mit den verschiedenen Verfahren der schriftlichen Subtraktion:
736 - 328
6002 - 4996
-
Wo sehen Sie Vor- und Nachteile der verschiedenen Verfahren?
Kann die Einführung schriftlicher Rechenverfahren auch Nachteile haben?
Die folgende Grafik illustriert das Ergebnis einer Untersuchung von Selter (2000), dass bei der Lösung der Aufgabe 701 - 698 (und anderer Subtraktionsaufgaben) das schriftliche Verfahren nach dessen Einführung von der Mehrzahl der Kinder genutzt wird.
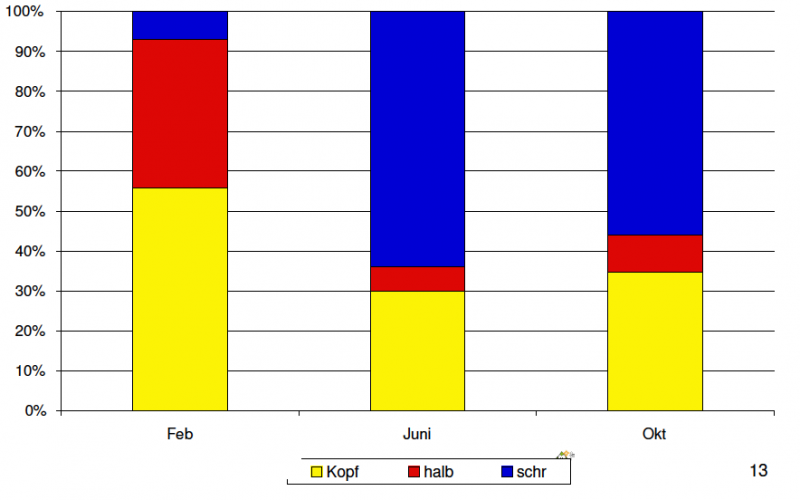(PIK AS 2010)
Aus diesem Ergebnis ergeben sich folgende Fragen: Warum verschwindet vielfach das Vertrauen der Kinder in ihre mündlichen Rechenkompetenzen, wenn sie den schriftlichen Algorithmus gelernt haben? Und warum werden beim halbschriftlichen Rechnen oft so viele Fehler gemacht? Eine mögliche Antwort könnte lauten: Häufig erhalten die Kinder wenig Gelegenheit, tatsächlich "eigene" Rechenwege zu entwickeln. Die halbschriftlichen Strategien werden ihnen vielfach - wie der schriftliche Algorithmus - "beigebracht".
Viele Kinder nutzen daher keine Rechenstrategien und Zerlegungsmöglichkeiten.
Eine weitere Frage lautet: Warum werden bei der Ausführung der schriftlichen Algorithmen so viele Fehler gemacht?
Eine mögliche Antwort ist: Die schriftlichen Rechenverfahren wurden von den Kindern auswendig gelernt. Eine "verständige" Ausführung des Algorithmus (des "Ziffernrechnens") ist ihnen nicht möglich, weil sie keine Beziehung zu den halbschriftlichen Strategien (zum "Zahlenrechnen") herstellen können.
Auf der nächsten Seite finden Sie Anregungen für eine verständige Einführung der schriftlichen Rechenverfahren im Unterricht.
