Was versteht man unter mathematische Begabungen und wie können sie erkannt werden?
Mathematisch interessierte, leistungsstarke und talentierte Kinder sind eine Bereicherung für den Mathematikunterricht. Diese Kinder angemessen zu fördern und auch mögliche mathematische Begabungen zu erkennen, das erleben Lehrpersonen als tägliche Fragestellung und Herausforderung.
Aus diesem Grund werden auf dieser Seite zunächst zu folgenden zentralen Punkten Hintergrundinformationen gegeben:
Zum Begriff "mathematische Begabung"
In allen neuen erziehungswissenschaftlichen und mathematikdidaktischen Veröffentlichungen wird davon ausgegangen, dass sowohl Erbe als auch Umwelt Einfluss auf die Entfaltung von Begabungen haben. Neben Begabungsmerkmalen zeigen Untersuchungen, dass es eine Reihe Persönlichkeitseigenschaften gibt, die eine Entfaltung von Begabungen positiv beeinflussen können (vgl. Käpnick 1998).
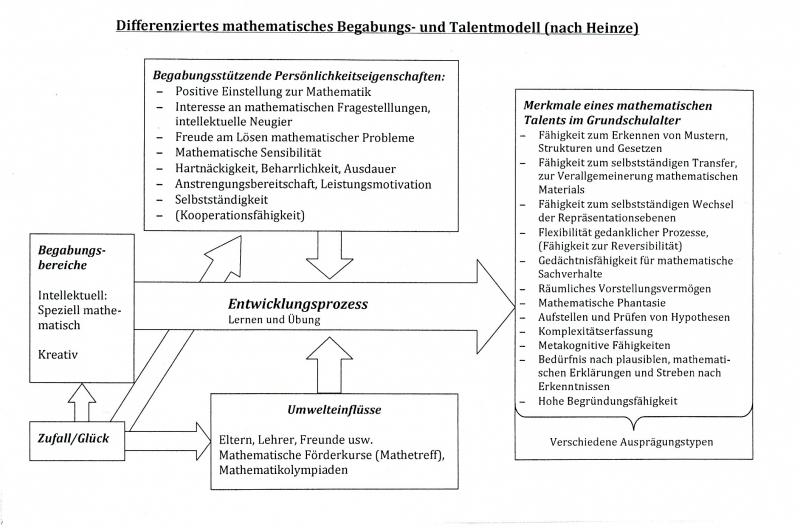Mathematische Begabungen (Heinze 2005)
Allerdings sind nicht alle Merkmale bei jedem begabten Kind ausgeprägt und hängen – wie bei allen Kindern – eng mit dem Interesse zusammen.
Ganz wichtig für die Lehrpersonen ist, dass auch zur Entfaltung von Begabungen Anregungen, Herausforderungen, Üben und vieles mehr notwendig sind. Werden diese Kinder nicht angemessen gefördert, also herausgefordert, kann das zu Entwicklungsproblemen bis hin zu Leistungsversagen und psychischen Störungen führen.
Erkennen mathematischer Begabungen
Zunächst einmal können Kinder im Unterricht auffallen – nicht dadurch, dass sie sehr schnell "rechnen", sondern durch kreative Lösungen, durch das selbständige Erkennen von Zusammenhängen und Strukturen (die wir vielleicht gar nicht gesehen haben), durch überraschende Begründungen und vieles andere mehr.
Aus einer einzigen kreativen Lösung kann zwar noch nicht auf eine mathematische Begabung geschlossen werden, aber diese mathematisch auffälligen Kinder sollte man weiterhin im Auge behalten und über einen längeren Zeitraum beim mathematischen Tätigsein beobachten. Immer wieder müssen sie angeregt werden, ihre Lösungen zu erläutern, zu erklären und zu begründen, auch wenn sie der Meinung sind, dass man das – die Lösung – doch sieht. Nur so gibt es eine Chance, sich den Denkweisen dieser Kinder zu nähern und ein Begabungspotential auszuloten.
Abgeleitet aus den Merkmalen mathematischer Begabung (vgl. Käpnick 1998, Heinze 2005) können folgende "Auffälligkeiten" im Unterricht auftreten, die Anlass für weitere Beobachtungen sein sollten:
-
Schnelle Auffassungsgabe, Langeweile bei Übungen und Wiederholungen
-
"Sehen" von Lösungen, wenig Aufschreiben
-
Kreative (unerwartete) Lösungen, divergentes Denken
-
Produktives, problemlösendes Denken
-
Streben nach Perfektion, mit eigenen Fehlern nicht zurechtkommen
-
Abstraktes Denken, Fähigkeiten zum Verallgemeinern
-
Enormes Vorwissen, meist sehr bereichsspezifisch
-
Komplexe Fähigkeiten
-
Intellektuelle Neugier, tiefe Interessen
-
uneigennützig und hilfsbereit
-
"Gefühl für Mathematik"
Natürlich werden nicht alle diese "Auffälligkeiten" bei begabten Kindern gleichermaßen zu beobachten sein. Bevor wir Kindern beim Lösen zuschauen und ihr Vorgehen analysieren, sollten Sie zunächst die folgende Aufgabe selbst bearbeiten:
Eigenaktivität
Schauen Sie sich das folgende Zahlenquadrat 30 Sekunden an. Decken Sie es dann zu und notieren Sie in einem 4x4-Quadrat alle Zahlen, die Sie sich merken konnten.
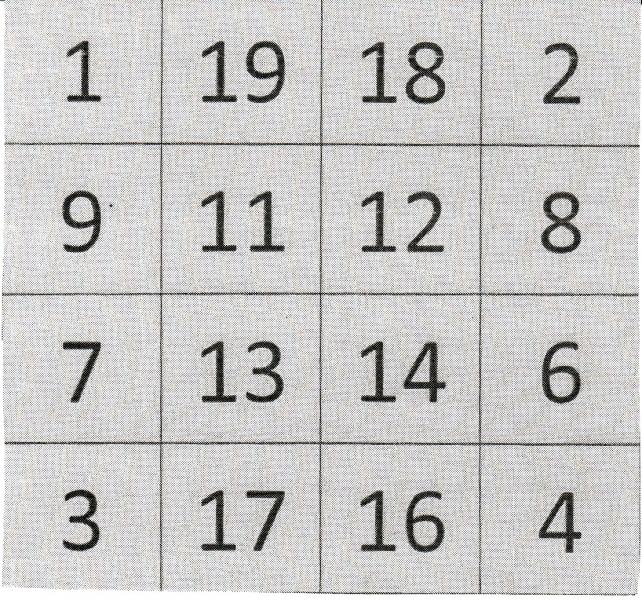
Vielleicht machen Ihre Kinder weitere Entdeckungen, wie z. B. Nina.
Eigenaktivität
Beobachten Sie Ninas Vorgehen. Welche Begabungsmerkmale können Sie erkennen?
Nina erläutert, wie sie sich die Zahlen gemerkt hat.
Ganz wesentlich ist, dass sich begabte Kinder bereits bei der Aufnahme von Informationen mathematische Zusammenhänge und Strukturen zu Nutze machen.
Das Zahlenquadrat bietet vielfältige Möglichkeiten, um das Denken der Kinder "sichtbar" werden zulassen. So können die Kinder zusätzlich aufgefordert werden, die Summe aller Zahlen des Quadrats möglichst geschickt zu berechnen. Welche Lösung haben Sie von Drittklässlern erwartet?
Eigenaktivität
Schauen Sie sich an wie Leon vorgeht.
Welche Begabungsmerkmale können Sie erkennen?
Leon errechnet die Summe
Es zeigt sich immer wieder, dass Kinder, die Aufgaben, wie die oben vorgestellten, hervorragend und in kürzester Zeit lösen, bei geometrischen Problemstellungen durchaus nicht die gleichen hervorragenden Leistungen zeigen. Es gibt die Inhaltsbereiche der Mathematik betreffend enorme Unterschiede zwischen begabten Kindern. Untersuchungen zeigen, dass es durchaus bereichsspezifische Begabungen innerhalb der Mathematik (arithmetische bzw. geometrische) geben kann. Krutezkij (1976) hat in seinen Untersuchungen zwischen drei Typen mathematischer Begabung unterschieden, nämlich zwischen einem algebraisch/arithmetischem Typ, einem geometrischen Typ und einem Mischtyp.
Die aufgezählten Begabungsmerkmale können uns im konkreten Unterricht helfen zu erkennen, in welchen Bereichen die besonderen Stärken mathematisch begabter Kinder liegen. Um die "Auffälligkeiten" (Merkmale) sichtbar werden zu lassen, sind entsprechende Aufgabenangebote im Unterricht erforderlich. Dazu möchten wir Ihnen auf der nachfolgenden Seite einige Anregungen für Ihren Unterricht geben. Für das Erkennen mathematischer Begabungen kann man auch die von Käpnick (1998) entwickelten Indikatoraufgaben nutzen. Das obige Zahlenquadrat gehört beispielsweise dazu.
An dieser Stelle finden Sie noch Ausführungen zu zwei Fragen, die im Zusammenhang mit (mathematischen) Begabungen immer wieder gestellt werden:
Zum dargestellten Thema möchten wir Sie auch auf die Seiten des Partnerprojetes KIRA verweisen. Sie können KIRA: Leistungsstarke Kinder für Erkundungen zu den Begabungsmerkmalen nutzen und erhalten dort weitere Informationen und Anregungen zum Thema "Leistungsstarke Kinder".
Diese Seite wurde erstellt von Marianne Grassmann für das primakom-Team.
