Hintergrund

Messkompetenz - Was ist das eigentlich?

Messen – was bedeutet das eigentlich? Eine Begriffsklärung

Die Beschaffung von Daten  aus der Realität kann ganz unterschiedlich realisiert werden. Dabei ist das Messen nur eine Möglichkeit diese Daten zu erhalten. Beim Messen wird mit Hilfe von Messinstrumenten ein direkter Vergleich mit einer festgelegten Einheit duchgeführt. Messungen sind durch diesen Messprozess naturgemäß einer Ungenauigkeit unterworfen. So ist beispielsweise die kleinste Maßeinheit auf dem Messbecher die Einheit Milliliter und damit wird der Wert beim Ablesen praktisch in diese Größeneinheit gerundet.
Auf dieser Seite wird der Messbegriff anhand physikalischer Größen näher erläutert.

Kurz gesagt bedeutet Messen festzustellen, wie oft ein Repräsentant einer als Einheit dienenden Größe in einem Repräsentanten einer anderen Größe gleicher Art enthalten ist.

Die Animation links zeigt, was die Definiton für den Größenbereich Länge bedeutet: Der Repräsentant, der als Einheit dient, ist der Stab, den die Figur in den Händen hält. Er passt viermal in den langen Stab; dem Repräsentanten einer anderen Größe gleicher Art.
Wichtig: Messen ist nicht mit Zählen gleichzusetzen!!

Eine weitere Möglichkeit Größen zu erhalten stellt das Schätzen dar. Beim Schätzen findet - anders als beim Raten - ein gedanklicher Vergleich mit bekannten Größen statt. Diese bekannten Größen können, in Abhängigkeit von den jeweiligen Stützpunktvorstellungen, der Inhalt einer Milchpackung oder die Breite einer Tür sein. Insofern ist das Schätzen eine Art von gedanklichem Messen.
Legt man bei Schätzen zusätzlich ein mögliches Maximum und Minimum des Schätzwertes fest, so wird an dieser Stelle vom Abschätzen gesprochen: "Der Schrank ist größer als die Tür, aber niedriger als die Decke."

Zu den Kernideen des Messens

Das Messen umfasst in allen Größenbereichen drei zentrale Kernideen, die wiederum als Prozess zu verstehen sind und im Weiteren näher erläutert werden.

Auswählen einer passenden Einheit

Gilt es ein Objekt zu vermessen, muss - abhängig vom Objekt - das passende Messgerät mit der dazu passenden Einheit gewählt werden. Die Länge des Klassenraums wird man also eher mit dem Tafellineal und weniger mit dem Geodreieck ausmessen. Und als Einheit bieten sich Meter und Zentimeter statt Kilometer und (Hekto-)Meter an. Das Gewicht des Schulranzens wird eher mit der Personenwaage als mit der Briefwaage ermittelt.

Das mehrfache und sachgerechte Verwenden dieser Einheit

Länge, Fassungsvermögen und Zeit eines Repräsentanten lassen sich über die mehrfache Verwendung eines Messobjekts ermitteln. Bezogen auf das obige Beispiel bedeutet dies, dass das Tafellineal am besten an einer Seite des Klassenraumes angelegt wird, damit auch wirklich die kürzeste Strecke ausgemessen wird. Das Tafellineal muss jeweils mit seinem einen Ende genau an dem Punkt angelegt werden, an dem das vorherige Messen endete. Es muss dann mitgezählt werden, wie oft das Lineal angelegt wurde.

Das systematische Zerlegen in Untereinheiten

Wird das auszumessende Objekt nicht hinreichend durch die auszumessende Einheit erfasst, so muss diese untergliedert werden.
Stellt man fest, dass nach mehrmaligem Aneinanderlegen das Tafellineal nicht ausreicht, um den Klassenraum auszumessen, weil eine kleine Lücke bleibt, muss noch eine kleinere Einheit dazu genommen werden. Passen würde die 10er-Stange der Cuisenairestäbe oder die 10er-Stange des Dienes Materials.

Die folgende Tabelle zeigt, was Messen konkret in den Größenbereichen bedeutet:

Längen

Um das Prinzip des Messens im Größenbereich Längen zu veranschaulichen, bietet sich das Messen von Strecken mit Meterstäben oder ein Meter lange Fäden an. Der Stab/ Faden wird so oft lückenlos an die Strecke gelegt, bis das Ende erreicht ist. Ist die Strecke aber noch ein Stückchen länger, aber zu kurz für das Anlegen eines weiteren Meterstabs, muss der Stab in die nächst kleinere Einheit zerlegt werden.

Zeitspannen

Im Größenbereich Zeitspannen können nur Vorgänge gemessen werden, die gerade in dem Moment, in dem gemessen werden soll, ablaufen. Ein schönes Beispiel ist der Hundertmeterlauf. Mit dem Startschuss startet man die Stoppuhr (analog und nicht digital). Mit jeder Sekunde streicht der Zeiger über einen Bereich auf der Skala. Die kann sich wie das nacheinander Umdrehen von lauter kleinen Sanduhren einer Sekunde vorstellen. Kommt der Läufer ins Ziel bevor die letzte Sanduhr durchgelaufen ist, muss die nächst kleinere Sanduhr/ Einheit gewählt werden.

Gewicht

Diese Definition lässt sich für die Größe Gewicht schön an einer Balkenwaage erläutern. Das zu wiegende Objekt liegt auf der einen Seite. Und es werden so lange gleich schwere Wägestücke auf die andere Seite gestellt, bis ein Gleichgewicht herrscht. Kommt dies nicht zu Stande, muss ein Repräsentant verkleinert werden.

Volumen

Im Größenbereich Volumen lässt sich das Prinzip des Messens mit Messbechern am besten veranschaulichen. Ein Eimer soll mit Wasser gefüllt werden. Man füllt nacheinander jeweils 1 Liter mit dem Messbecher in den Eimer. Ist der Eimer am Ende noch nicht ganz voll, würde aber überlaufen, wenn man einen weiteren Liter hinzugießt, dann wählt man einen kleineren Messbecher, also die nächstkleinere Einheit.

Welche Wissensebenen sind mit dem Messverständnis verknüpft?

Als Lehrkraft ist es wichtig über die oben dargestellten Wissensebenen Bescheid zu wissen, um bei Schwierigkeiten adäquat reagieren zu können. Das folgende Schaubild stellt die drei Wissensebenen dar. Details über die Wissensebenen können Sie bei Ruwisch (2015, S. 2f) nachlesen.

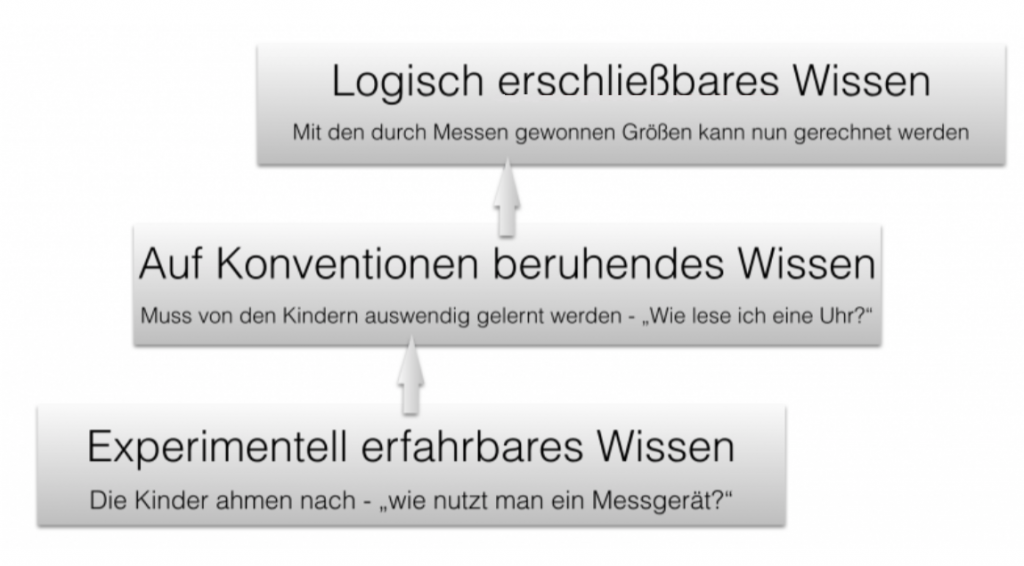
Zu einem umfassenden Messverständnis gehören viele Komponenten, die eng miteinander verknüpft sind. Es wird deutlich, dass diese Komponenten unbedingt im Unterricht thematisiert und systematisiert werden müssen.

Eigenaktivität

Überlegen Sie: "Wie ist die Berliner Uhr von der Einstiegsseite zu lesen? (Hinweis: Die Uhr zeigt gerade 10.31 Uhr an.)

Kommentar zur Eigenaktivität

Die Anzeige der Zeit erfolgt in einem Stellenwertsystem zur Basis 5. Die Stunden und Minuten werden durch leuchtende Segmente in vier waagerecht untereinander angeordneten Streifen dargestellt. In der ersten, zweiten und vierten Zeile sind vier und in der dritten elf Leuchten angebracht. Die ersten beiden Zeilen zeigen mit roten Leuchten die Stunde an, wobei im oberen Streifen ein leuchtendes Segment für fünf Stunden und im unteren für eine Stunde steht. Die aktuelle Stunde ergibt sich aus der Addition der Werte. Entsprechend werden in den beiden unteren Zeilen die Minuten mit gelben Segmenten in Fünfer- und Einerschritten angezeigt. Die Leuchten für 15, 30 und 45 Minuten sind zur besseren Ablesbarkeit rot. Über den Zeilen leuchtet eine runde Leuchte im Zwei-Sekunden-Takt auf.

Die Uhr zeigt also 10.31 Uhr an.

Wie entwickelt sich das Messverständnis?

Mathematisch hängen das Größen- und das Zahlverständnis eng miteinander zusammen. Doch sind die Vorerfahrungen der Kinder zum Messen von Größen deutlich heterogener als in der Arithmetik. Um diese unterschiedlichen Vorerfahrungen besser einordnen zu können, ist es wichtig zu wissen, wie sich das Messverständnis entwickelt.

• Grundlegendes Verständnis von Eigenschaften - Durch das Messen gewinnt man Größen. Und Größen sind, vereinfacht ausgedrückt, Eigenschaften von realen Objekten, die in Zahlen ausgedrückt werden können. Diese zu messenden Eigenschaften müssen dem Kind natürlich bekannt sein. Auch die damit verbundenen Adjektive und deren Steigerungsformen müssen bekannt sein, z. B. "lang, länger, am längsten".

• Invarianz und Transitivität - Eine Größe eines Objekts bleibt erhalten, wenn sich beispielsweise seine Lage im Raum ändert. Ein Wollfaden mit einer Länge von zehn Zentimetern behält seine Länge, auch wenn ich ihn zu einem Kneul forme. Weiterhin ist das Verständnis von Transititvität für das Messverständnis von großer Bedeutung. Ein junges Kindergartenkind ist kleiner als einen Meter und ein Schulkind ist größer als einen Meter. Somit ist das Schulkind größer als das Kindergartenkind.

• Regelmäßiges Untergliedern einer Größe - Ein Kind muss in der Lage sein, einen Gegenstand gedanklich in mehrere gleichgroße Teile zu zerlegen. Und in der Umkehrung muss es sich sicher sein, dass das Zusammensetzen dieser Teilgrößen wieder die Ausgangsgröße ergibt.

• Mehrfaches Verwenden einer Maßeinheit - Beispiel: "Wie viele Eimer Wasser brauche ich um eine Badewanne zu füllen?". In diesem Beispiel wird der Eimer als Maß gewählt. Dieser muss so lange mit Wasser befüllt werden und in die Wanne geleert werden, bis die Wanne voll ist.

• Zahlenmäßiges Erfassen der Messhandlung - Um am Wannenbeispiel anzuknüpfen; um nun herauszufinden, wie viele Eimer Wasser benötigt werden um eine Wanne zu füllen, müssen die Eimer gezählt werden, die in die Wanne geschüttet werden. Die letzte Zählzahl muss dann als Maßzahl verstanden werden.

• Beliebige Skalenpunkte als Ausgangspunkt eines Messprozesses - Beim Messen mit Messgeräten muss man nicht unbedingt bei Null starten. Durch Differenzbildung kann jeder beliebige Punkt der Skalen als Ausgangspunkt genutzt werden. Sehr schön deutlich wird das am Ziffernblatt der Uhr. Die Uhr ist eigentlich nicht dazu da um Zeitspannen zu messen sondern sie gibt Zeitpunkte an. Durch Differenzbildung kann aber eine Zeitspanne zwischen zwei Zeitpunkten berechnet werden.

• Maßzahlen als Beziehung zwischen Einheit und Zahlenwert - Messen ist mehr als Zählen. Maßzahlen sind immer mit Bezug auf eine ausgewählte Einheit zu interpretieren. Dies bedeutet auch, dass die Größe eine Objekts durch verschiedene Zahlen und den dazugehörigen Einheiten bezeichnet werden kann.

Die Komplexität des Messverständnisses macht deutlich, dass Messen auch selbst zum Unterrichtsgegenstand gemacht werden muss. Auf der nächsten Seite werden daher verschiedene unterrichtliche Vorschläge gemacht.