Kinder forschen operativ
In dem folgenden Film sehen Sie, wie zwei Erstklässler mit dem Spiegeltangram (vgl. Knapstein u.a. 2005) arbeiten (das Material wird im Film erklärt). Die Kinder müssen versuchen, zwei Dreiecke passend vor dem Spiegel zu platzieren, sodass das Spiegelbild mit den gelegten Dreieecken einem Bild auf einer Kartendarstellung entspricht.
Aber ich hab ja gar nicht zwei Grüne?!
Der Lehrplan der Grundschule in NRW verlangt, dass das Üben im Mathematikunterricht u.a. operativ strukturiert sein soll (vgl. MSW NRW 2008, S. 55).
Dies meint, dass die Kinder an geeigneten Materialien Handlungen vornehmen, dabei Erkenntnisse gewinnen und diese weiter anwenden. Leider wird diese Forderung häufig vollkommen missverstanden, so dass nahezu jede körperliche Tätigkeit oder Handlung der Kinder als "operativ" bezeichnet wird. Dem ist aber nicht so.
Auch die Kinder im Video gehen operativ vor, d.h. sie erforschen, wie sie die beiden Dreiecke auf unterschiedliche Art und Weise vor dem Spiegel oder vor sich auf dem Tisch platzieren können.
In Kontext des operativen Prinzips muss und sollte man sich nun fragen: Was sind die Objekte, die die Kinder erforschen? Was sind die Operationen, die sie mit den Objekten durchführen? Und was sind die Wirkungen, die sie damit erzielen?
Im Folgenden soll ein wenig Klarheit geschaffen werden, was das operative Prinzip bedeutet und welche Rolle es im Mathematikunterricht einnimmt. Dafür wird auf die folgenden Punkte eingegangen:
Das „operative Prinzip" geht zurück auf die Lerntheorie von Piaget und Aebli. Es wird häufig auch als "verinnerlichtes Handeln" bezeichnet. Piaget und Aebli beschränkten sich aber lediglich auf das Verständnis und die Verinnerlichung von Operationen. So sollen die Kinder beispielsweise durch konkrete Handlungen am Material verstehen, was für eine Vorstellung hinter der Rechenoperation "Plus" steckt: 4+5 bedeutet z.B. man hat vier Plättchen und legt noch fünf dazu. "Dazulegen" ist hier die entsprechende Vorstellung der Operation "Plus". „Manipuliert der Schüler nur sinnlos, versteht er nicht, was er tut, durchschaut er die Struktur der Handlung nicht, so nützt es ihm auch nicht, sich die Manipulationen, die er vollzogen hat, vorzustellen" (Aebli 1976, S. 142). Aebli fordert daher, dass die Kinder z.B. mit den Plättchen nicht einfach irgendwas machen sollen, sondern verstehen sollen, welche Rechnung zu ihrer Handlung gehört (genauso natürlich auch umgekehrt: welche Handlung gehört zur Rechnung?).
Wittmann hat in den 80er Jahren das operative Prinzip auf die Mathematikdidaktik ausgeweitet, indem er es von den dynamischen Operationen auf die vermeintlich statischen Objekte ausdehnte (vgl. Wittmann 1985). Nach Wittmann reicht es nämlich nicht aus, sich im Mathematikunterricht ausschließlich auf die Erforschung und das Verständnis der Operationen an sich zu beschränken, sondern er muss ebenso auf die Objekte eingehen, auf welche die Operationen angewandt werden, um deren Eigenschaften und Beziehungen zueinander zu untersuchen, denn andernfalls kann auch von den Operationen nur ein unvollständiger Begriff aufgebaut werden (vgl. Wittmann 1983, S. 269). Er fordert daher, dass die Schülerinnen und Schüler mit Hilfe von Handlungen an geeigneten Materialien bzw. mit den konkrekten Objekten neue Erkenntnisse gewinnen und bestehende Vorstellungen revidieren, ausbauen oder stützen. „Objekte erfassen bedeutet, zu erforschen, wie sie konstruiert sind und wie sie sich verhalten, wenn auf sie Operationen (Transformationen, Handlungen, ...) ausgeübt werden. Daher muss man im Lern- und Erkenntnisprozess in systematischer Weise:
1. untersuchen, welche Operationen ausführbar und wie sie miteinander verknüpft sind,
2. herausfinden, welche Eigenschaften und Beziehungen den Objekten durch Konstruktion aufgeprägt werden,
3. beobachten, welche Wirkungen Operationen auf Eigenschaften und Beziehungen der Objekte haben (was geschieht mit ..., wenn ...?)" (Wittmann 1985, S. 9)
Die Kinder sollen demnach eine forschende Grundhaltung entwickeln und ihren Blick „auf das Verhalten der Eigenschaften, Beziehungen und Funktionen der Objekte bei den transformierenden Operationen gemäß der Frage „Was geschieht mit…, wenn…?“ [richten] (operatives Prinzip)“ (Wittmann 1981, S. 79). Das kann im Unterricht in sehr vielfältiger Hinsicht passieren, wie die folgenden Beispiele zeigen.
Das so genannte Nim-Spiel, weitere Informationen dazu finden Sie auf unserer Partnerseite KIRA: Nim-Spiel (in Anlehnung an Müller & Wittmann 1985, S. 230), eignet sich sehr gut zur Anleitung des operativen Denkens bei Kindergarten- und Grundschulkindern. Falls Sie das Spiel nicht kennen, sollten Sie sich zunächst den Internetauftritt zum Nim-Spiel ansehen.
In der folgenden Eigenaktivität sollen Sie das Video der Kindergartenkinder Konrad und Sönke betrachten. Zu bemerken ist an dieser Stelle, dass die Kinder bisher keinerlei Erfahrungen damit haben, ihre eigenen Gedankengänge zu verbalisieren. Dennoch können Sie deutlich erkennen, dass die Kinder nicht einfach "irgendwas" machen. Sie spielen durchaus vorausschauend und erlangen aus ihren Handlungen sehr schnell Einsichten in die Gewinnregel des Spiels.
Eigenaktivität
Konrad und Soenke
1. Inwieweit analysieren die Kinder während des Spiels ihre eigenen Handlungen:
-
Wie viele Plättchen sollte der Spielpartner auf das Feld legen, damit man selbst gewinnen kann? („Leg noch ein Plättchen")
-
Was wäre gewesen, wenn der Spielpartner an einer bestimmten Stelle eine andere Anzahl an Plättchen gelegt hätte? Wie wäre das Spiel dann verlaufen?
-
Wie hätte das Spiel verlaufen müssen, damit man selbst und nicht der Spielpartner gewinnt?
-
Welche Felder sollte man erreichen, damit man sicher gewinnt?
2. Wie werden die Entdeckungen auf den Spielplan bis 12 übertragen?
3. Inwieweit wird aus diesem Video ersichtlich, dass sich die Kinder während der gesamten Beschäftigung mit dem Spiel im operativen Denken üben? Was sind die Objekte, die sie erforschen? Was sind die Operationen, die sie ausführen? Was sind die Wirkungen, die sie erkennen?
Es gibt diverse weitere Aufgabenformate, die das operative Denken der Kinder anregt. So z.B. auch das Aufgabenformat "Summen auf der Hundertertafel" (vgl. Floer 2003). Hierbei sollen die Kinder beispielsweise die Summe eines quadratischen Ausschnitts (der Größe 2x2) bestimmen.
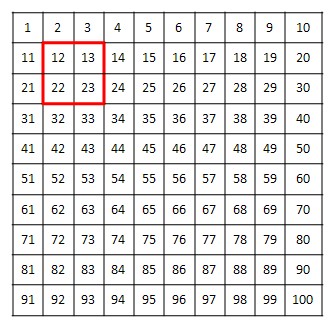
Anschließend wir der Ausschnitt um eine Einheit nach rechts bzw. nach unten oder links verschoben. Die Frage, die die Kinder hierbei beantworten sollen, ist die folgende: "Was passiert mit der Summe, wenn du den Ausschnitt um eine Einheit nach rechts (nach unten, nach links) verschiebst?"
Eigenaktivität
Schauen Sie sich die Videos der beiden Viertklässler Thomas und Timo an.
1. Inwiefern sind bei den beiden Kindern operative Vorgehensweisen beobachtbar?
2. Was sind die Objekte, die sie erforschen? Was sind die Operationen, die sie ausführen? Was sind die Wirkungen, die sie erkennen?
Thomas
Timo
Weiterführende Analysen
Schöne Päckchen
Auch die Schönen Päckchen (vgl. Wittmann & Müller 2004) erfüllen das operative Prinzip, da die Kinder hier aufgefordert werden, in systematischer Weise Rechenoperationen zu untersuchen: Wenn der erste Summand um Eins erhöht wird, dann ... . Wenn der erste Summand um Eins erhöht und der zweite um Eins verringert werden, dann ... .
Bei den Schönen Päckchen passiert es aber häufig, dass die Kinder nur von oben nach unten also spaltenweise und nicht zeilenweise schauen (vgl. nachstehende Abbildung, entnommen von der Seite unseres Partnerprojekts PIKAS, siehe 6. Verwandte Themen: "Entdeckerpäckchen" ).

Die Kinder entdecken nicht zwangsläufig, dass es einen Zusammenhang zwischen der systematischen Veränderung der Summanden und der Veränderung der Summe gibt. Stattdessen beobachten sie nur, dass sich die Summanden verändern und die Summe auch, aber erkennen nicht unbedingt die "Wenn-dann" - Beziehung (Wenn der erste Summand um Eins größer und der zweite um Eins kleiner wird, dann bleibt die Summe gleich.)
Eigenaktivität
Schauen Sie sich auch die Videos auf der Seite unseres Partnerprojekts KIRA: Schöne Päckchen an und analysieren Sie, an welchen Stellen die Kinder anfangen (ggf. auch durch einen Impuls der Interviewerin), den Zusammenhang von Summanden und Summen bzw. Minuend und Subtrahend und Differenz zu erfassen.
Was sind hier im Sinne des operativen Prinzips die Objekte, die Operationen und die Wirkung, die die Kinder untersuchen?
Achsensymmetrie
Wie im obigen Einstiegsbeispiel gezeigt, können bei der Arbeit mit dem Spiegeltangram je nach Strategie verschiedene operative Handlungen beobachtet werden. Mal untersuchen die Kinder was passiert, wenn sie mit einem oder auch mehreren der geometrischen Formen vor dem Spiegel operieren, mal untersuchen sie, was passiert, wenn sie verschiedene geometrische Formen auf unterschiedliche Art und Weise zusammenlegen.
Schauen Sie sich auch die Videos bei unserem Partnerprojekt KIRA: Achsensymmetrie an und analysieren Sie, abhängig von der jeweiligen Strategie des Kindes, welches Objekt bzw. welche Objekte das Kind untersucht, welche Operationen es ausführt und welche Wirkungen es erzielt.
Was kann bei dem jeweiligen Kind die Wenn-dann-Beziehung sein, die es betrachtet? Dabei können Sie sich an dem obigen Einstiegsbeispiel orientieren bzw. die Kommentare im Film als Orientierung nehmen!
Verwandte Themen
Ein Beispiel für den inklusiven Unterricht zum Erforschen operativer Veränderungen an Zahlenmauern auf Grundlage unterstützender und weiterführender Aufgabenstellungen finden Sie auf der Seite unseres Partnerprojekts Mathe inklusiv.