Unterricht

Wie kann man mit Guten Aufgaben Guten Unterricht machen?

Im Hintergrund haben Sie erfahren, welche Kriterien Gute Aufgaben erfüllen sollen. Auch wurde herausgestellt, dass mit Hilfe der Streichholzvierlinge diese Kriterien erfüllt werden können und welche Aufgabenvariationen ergänzend möglich sind, um diese Gute Aufgabe weiter auszureizen.
Im Folgenden wird nun die konkrete Umsetzung dieser Guten Aufgaben vorgestellt. Die Aktivitäten sind für die zweite oder auch dritte Schulstufe angemessen.

Bausteine einer Unterrichtsreihe mit Streichholzvierlingen

Die einzelnen Bausteine der Unterrichtsreihe gliedern sich methodisch-didaktisch jeweils in zyklische Phasen des gemeinsamen Beginns, der individuellen sowie gemeinsamen Erkundung und der gemeinsamen Analyse- und (Zwischen-)Reflexion im Sinne praktizierter Mathekonferenzen und darauf basierter Weiterarbeit.

Sie gliedern sich in folgende Aktivitäten, die auf dieser Seite konkretisiert werden:

1. Vorstellen des Figurentyps und entdecken der Bauregel
2. Finden möglichst vieler Vierlinge durch die Kinder
3. Kennenlernen eines Spiels mit den Vierlingen mit Reflexion von Spielstrategien
4. Bearbeiten von schriftlichen Forscheraufgaben

Vorstellen des Figurentypus und entdecken der Bauregel

Im Sitzkreis wird den Kindern gesagt, dass in den kommenden Unterrichtsstunden mit den Streichholzvierlingen gearbeitet werden soll. Es wird allerdings nicht einfach gesagt, was ein Streichholzvierling ist. Das sollen die Kinder selbst herausfinden.
Anschließend werden mit den Worten „Das sind Streichholzvierlinge.“ einige Vierlinge in die Mitte des Sitzkreises gelegt (dazu z.B. vergrößerte Stäbe bzw. Holzstifte mitbringen).
Dann werden mit den Worten „Das sind keine Streichholzvierlinge.“ unpassende Vierlinge in die Mitte gelegt, z.B. folgende Vierlinge:

Anschließend sollen die Kinder vermuten, wie die Bauregel für Streichholzvierlinge lautet. Eine kurze Murmelphase unter den Kindern kann hilfreich sein, damit auch alle Kinder eine grobe Idee von der Bauregel haben und sich an der anschließenden Sammelphase beteiligen könnten.
In dieser Sammelphase können die Kinder weitere Vierlinge oder auch Nicht-Vierlinge selber legen und daran die Bauregel zeigen. Die Lehrperson hilft, die Entdeckungen der Kinder ggf. fachsprachlich umzuformulieren und gemeinsam mit den Kindern an der Tafel festzugehalten.

Anschließend muss noch geklärt werden, wann Vierlinge als gleich oder verschieden gelten. Dazu werden z.B. folgende drei Vierlinge z.B. auf quadratische Zettel in die Mitte gelegt:

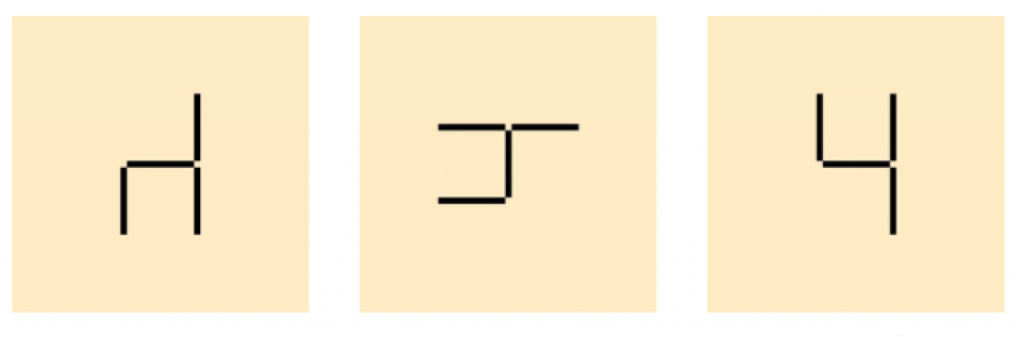
Durch Drehen der quadratischen Zettel können die Kinder erkennen, dass die Vierlinge 2 und 3 identisch sind. Durch Drehung kann man sie so hinlegen, dass sie exakt gleich aussehen. Vierling 1 ist das Spiegelbild der anderen beiden. Da diese verändert werden müssten, um so auszusehen wie Vierling 2 oder 3, gelten sie als verschieden.
An weiteren Beispielen kann überprüft werden, ob die Kinder diese Unterscheidungsidee verstanden haben.

Finden möglichst vieler verschiedener Vierlinge

Die Kinder werden anschließend aufgefordert, möglichst viele Streichholzvierlinge zu finden. Dazu bekommen sie möglichst in Partnerarbeit Hölzer sowie quadratische Zettel. Diese können sie einerseits nutzen, um mögliche Drehungen nicht im Kopf durchführen zu müssen. Dazu legen sie die Hölzer auf das Blatt Papier und drehen es. Andererseits können sie auf diesen Zetteln gefundene Vierling aufzeichnen.
Die Lehrkraft kann unterstützend einwirken und z.B. bei sehr großen Schwierigkeiten von einzelnen Kindern oder Kinderpaaren einen Beraterkreis einberufen: die Kinder, die nicht wissen, wie sie vorgehen können oder z.B. noch sehr große Schwierigkeiten beim Zeichnen haben, treffen sich mit der Lehrperson im Sitzkreis. Dort werden in Unterstützung durch die Lehrperson Vierlinge gefunden und gemeinsam aufgezeichnet.

Schnellere Kinder, die der Meinung sind, alle Vierlinge schon gefunden zu haben, können im Austausch mit weiteren Mitschülerinnen oder Mitschülern herausfinden, ob die anderen Kinder die gleichen Vierlinge gefunden haben, wie sie. Alle gefundenen Vierlinge werden auf einem DinA-3 Zettel gesammelt. Zudem können die Kinder dazu angeregt werden, die Vierling so zu sortieren, dass man erkennt, dass oder ob es wirklich alle sind.

In der anschließenden Reflexionsphase werden sowohl alle Vierlinge an der Tafel gesammelt, Strategien besprochen und geklärt, warum es nur 25 Vierlinge sein können. Werden nicht alle 25 Vierlinge von den Kindern gefunden, werden die letzten noch fehlenden Vierlinge gemeinsam an der Tafel ergänzt.

Das Spiel: Vierlino

In der nächsten Unterrichtsstunde spielen die Kinder mit den Vierlingen ein Spiel:
Die Karten werden gemischt. Jeder Spieler bekommt 5 Karten. Eine Karte wird als Ausgangskarte offen in die Tischmitte gelegt. Der darauf abgebildete Streichvierling wird mit Streichhölzern daneben nachgelegt. Reihum sind die Spieler nun am Zug und versuchen ihre Karten „loszuwerden“. Dazu müssen sie sich vorstellen, ob und wie sie durch das Umlegen von genau einem Streichholz einen Streichholzvierling erzeugen können, den sie auf der Hand halten. Wer als erster seine Karten losgeworden ist, hat gewonnen.
Als Hilfestellung kann das probeweise Versetzen und Drehen des Vierlings erlaubt werden.
Der Lehrkraft kommt hierbei eine stark beobachtende Rolle zu: Welche Spielsituationen waren schwierig? Warum? Welche Kinder erkennen sehr schnell, wie sie umlegen können? Wie schaffen sie das möglicherweise (ggf. müsste man die Kinder hierzu schon befragen)?
Nach einigen Spielrunden wird das Spiel gemeinsam im Sitzkreis gespielt und Spielstrategien besprochen: Wie kann man schnell erkennen, ob ein Vierling sich durch Umlegen eines Holzes aus einem anderen erzeugen lassen kann? Eine mögliche Strategie wäre, zu erkennen, ob zwei Vierlinge bereits in drei Hölzern übereinstimmen. Das folgende Beispiel illustriert diese Idee:

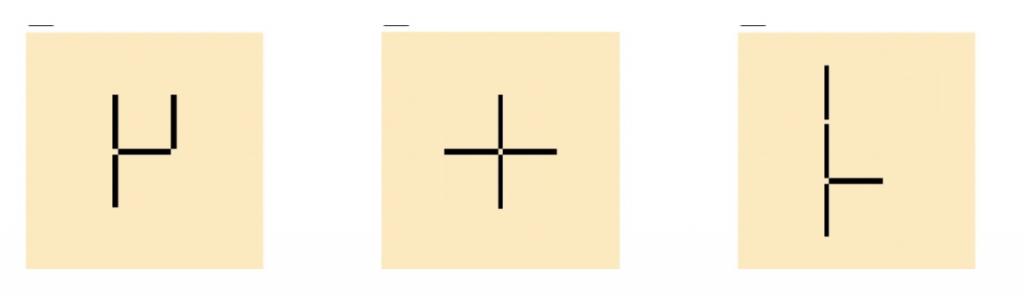
Diese drei Vierlinge können alle ineinander umgebaut werden, da sie in drei Hölzern übereinstimmen. Die jeweiligen drei identischen Hölzer (der jeweilige identisch Drilling) sollte von den Kindern gezeigt werden, damit auch schwächere Kinder die Strategie verstehen.
Zudem kann es in der Spielsituation passiert sein, dass ein Kind den „Strich“ als Vierlinge hatte, und diesen nicht ablegen konnte.

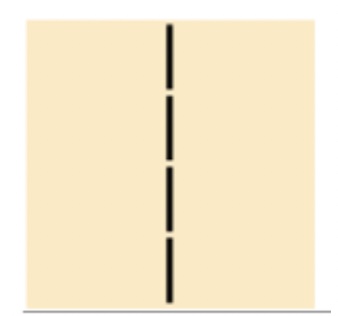
Falls diese Situation vorab zu beobachten war, kann darüber gesprochen werden, warum diese Karte im Spiel nur schwer abzulegen ist. Aus ihr können nur die Vierlinge mit drei Hölzern in einer Reihe gelegt werden. Davon gibt es aber nur sehr wenige.

Forscheraufträge zur Vertiefung

Auf der Website des Partnerprojekte PIKAS finden Sie viele verschiedene Arbeitsblätter zur Vertiefung der Spielstrategien Vierlino. Einige werden hier exemplarisch näher analysiert:

Welche Vierlinge kannst du erzeugen?

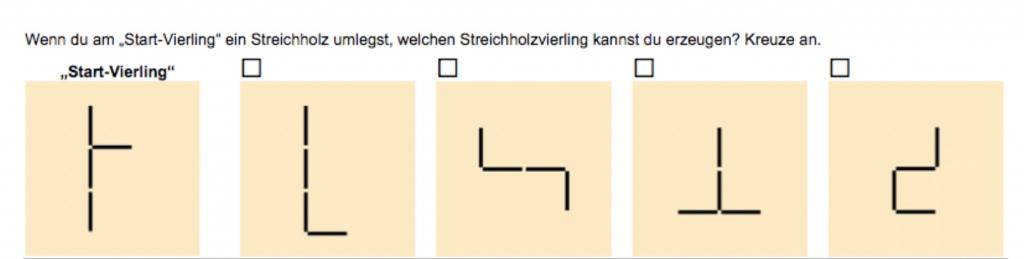
Bei diesem Arbeitsblatt können die Kinder nochmals vertiefend erfahren, dass sich Vierlinge nur ineinander umbauen lassen, wenn sie in genau drei Hölzern übereinstimmen. Die gemeinsamen Hölzer können z.B. farbig markiert werden.

Streichholzvierlinge systematisch untersuchen

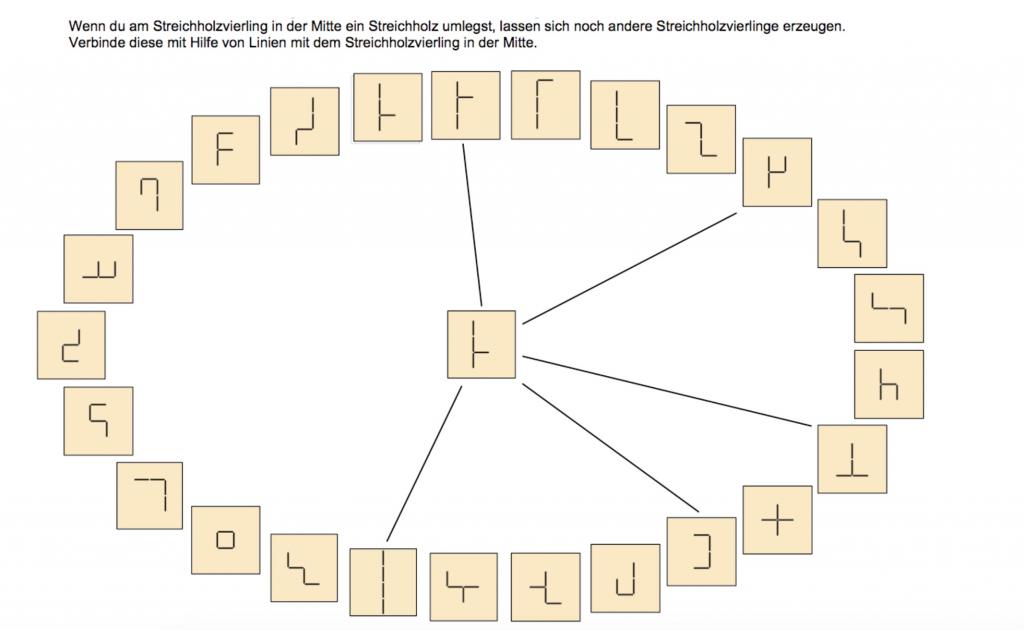
Mit Hilfe eines solchen Arbeitsblattes kann gezielt untersucht werden, ob manche Vierlinge sehr viele oder nur wenige Ablegemöglichkeiten im Spiel haben. Die Kinder können erkennen, dass Vierlinge, die verschiedene Drillinge in sich tragen, auch viele verschiedene Ablegemöglichkeiten haben.

Wie kannst du einen Mitspieler blocken?

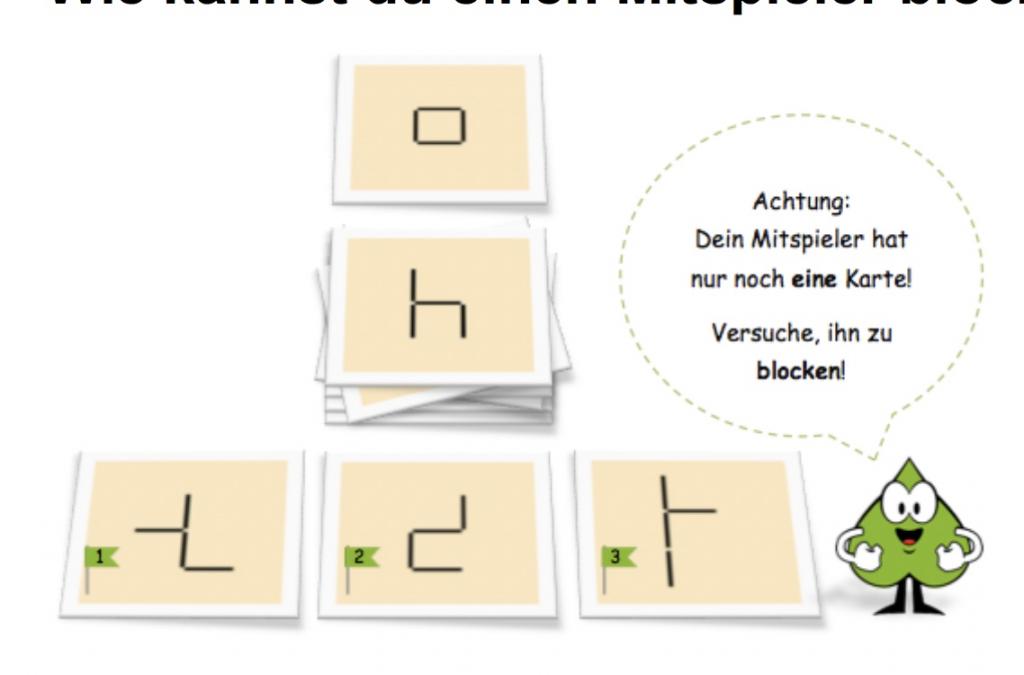
Mit diesem Arbeitsblatt kann das vorausschauende Spielen angeregt werden. Die Kinder müssen mehrere Umlegeschritte mental verarbeiten, um die Frage beantworten zu können.

Diese Seite wurde auf der Grundlage eines Skripts von Tobias Huhmann für das primakom-Team erstellt.