Kinder in Lösungsprozessen unterstützen
Guter Mathematikunterricht ist längst kein reiner Rechenunterricht mehr. Neben bzw. zum Erlernen der rein rechnerischen Fähigkeiten ist das Ziel, dass Kinder Muster und Strukturen in unterschiedlichen mathematischen Kontexten entdecken und dabei Beziehungen und Zusammenhänge nutzen, um arithmetische aber auch geometrische Problemstellungen oder Sachsituationen bearbeiten zu können.
Und genausowie das Rechnen selbst müssen Kinder auch das Problemlösen, oder allgemein das Erkennen und Nutzen von Zusammenhängen und Beziehungen in verschiedenen mathematischen Kontexten, erst erlernen, indem sie sich in vielfältigen Situationen in diesem Versuchen und Üben. Dabei sollten sie unterschiedliche Strukturen und Zusammenhänge zu erkennen und nutzen aber auch, rechnerische Fähigkeiten zu festigen und zu automatisieren.
In Anlehnung an diese Einleitung und die ersten Fragen aus dem Einstieg soll auf dieser Seite folgenden Punkten nachgegangen werden:
Zum Einstieg...
Eigenaktivität
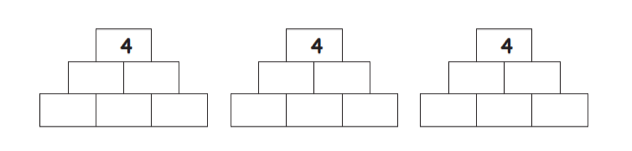
Finden Sie (alle) Zahlenmauern mit der Zielzahl 4.
Überlegen Sie, wie Sie vorgehen können, um eine und dann möglichst alle Lösungen zu finden
Im mathematischen Sinne bezieht sich der Begriff „Lösung“ auf die Bewältigung einer (inner-)mathematischen Aufgabenstellung oder mathematischen Sachsituation. Hinter (Problem-)Lösungsprozessen, egal ob simpel oder komplex, stecken dabei mehrschrittige Prozesse. Mit der folgenden Abbildung kann auch schon Kindern deutlich werden, welche Schritte notwendig sind, um problemhaltige Aufgaben zu lösen bzw. anzugehen.Es wird deutlich, dass das Verstehen der Aufgabe die gar nicht so triviale erste Anforderung darstellt und der Problemlöseprozess mit dem Aufstellen eines Ergebnisses noch nicht abgeschlossen ist.
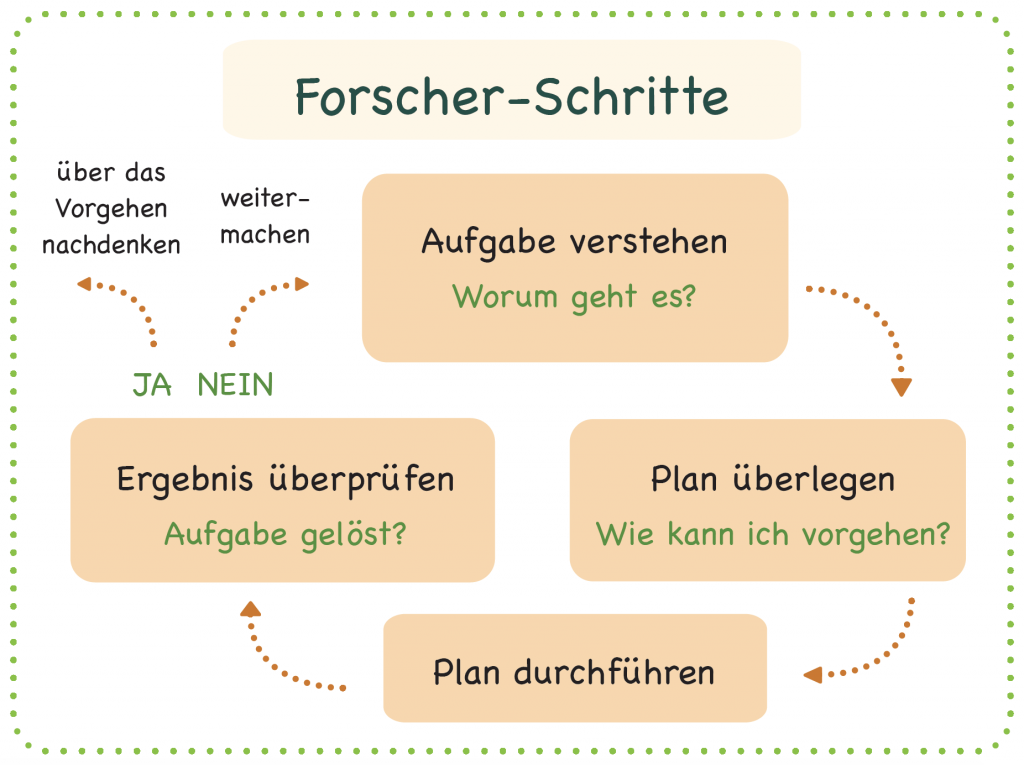 Die Abbildung ist ein Ausschnitt des Plakats „Das nutzen Mathe-Forscher“ von PIKAS (pikas.dzlm.de/node/556).
Die Abbildung ist ein Ausschnitt des Plakats „Das nutzen Mathe-Forscher“ von PIKAS (pikas.dzlm.de/node/556).
Ein Problem liegt dann vor, wenn die vorhandenen bzw. gegenwärtig aktivierbaren Kenntnisse und Fähigkeiten zur Lösung einer Aufgabenstellung noch nicht ausreichen, und dabei eine prinzipiell überwindbare Barriere zum gegenwärtigen Zeitpunkt die Lösung verhindert. Solche Schwierigkeiten können an unterschiedlichen Stellen des Prozesses auftreten.
Dabei entstehende Schwierigkeiten bzw. die Barrieren selbst sind individuumsspezifisch, das bedeutet, sie können von Kind zu Kind unterschiedlich ausfallen (je nach Kentnissen und Fähigkeiten). Das bedeutet, dass nicht jede Aufgabe für jedes Kind zum gleichen Zeitpunkt eine Problemlöseaufgaben darstellt. Aufgaben, die mit vom Kind bereits erarbeiteten Routineverfahren (Schema, Plan, Regel, Formel) gelöst werden können, sind zu ‚leicht’. Aufgaben, für die seine vorhandenen Kenntnisse und Fähigkeiten keinen geeigneten Ausgangspunkt darstellen oder weil die zur Aufgabenlösung benötigten Kenntnisse nicht aktiviert werden können, ‚zu schwer‘. Es hängt also stark von den individuellen Kenntnissen und Fertigkeiten der/des potenziellen Problemlösenden ab, inwiefern sie für das jeweilige Kind eine Problemlöseaufgabe ist, oder nicht. Da Klassen allgemein sehr heterogen sind, gilt es dies bei der Auswahl von (Problemlöse)Aufgaben zu beachten.
In diesem Zusammenhang kommen den substantiellen/guten Aufgaben eine zentrale Rolle zu (vgl. Aufgabenformate). Diese
-
basieren auf mathematisch reichhaltigen Kontexten (mit oder ohne Wirklichkeitsbezug), die es ermöglichen, inhaltsbezogenen und prozessbezogene Kompetenzen zu schulen,
-
bieten unterschiedliche Problemstellungen mit verschiedenen Schwierigkeitsgraden, die – auf dem jeweiligen Niveau – in unterschiedlichen Schuljahren eingesetzt werden können,
-
sind innerhalb eines bestimmten Problemkontextes offen genug, um Bearbeitungen einzelner Schüler auf unterschiedlichem Niveau zu ermöglichen.
Auch Problemlöseaufgaben sollten diese Kriterien erfüllen, um der Heterogenität der Kinder gerecht zu werden.
Eigenaktivität
Erinnern Sie sich an die Aufgabe aus dem Einstieg:

Warum handelt es sich bei der Ausgangsaufgaben zur Zielzahl 4 um eine „gute Problemlöseaufgabe“? Welche Kriterien werden erfüllt?
Problemhaltige Aufgaben sollten sich dabei, wie oben angedeutet, nicht auf den Bereich der Arithmetik beschränken. Auch in den anderen Inhaltsbereichen ergeben sich immer wieder Möglichkeiten, das Problemlösen und Argumentieren zu fordern und zu fördern. Alle Inhaltsbereiche müssen auch im Hinblick auf das Problemlösen angesprochen werden, da sich nur so ein differenziertes Bild von und Verständnis für Mathematik entwickeln kann. Hier finden Sie zu jedem Aufgabenbereich eine mögliche Aufgabenstellung .
Lösungsprozesse systematisieren lernen
Was sind mögliche Problemfelder?
Doch nicht allen Kindern gelingt es ohne Unterstützung, Problemlöseaufgaben zu bearbeiten. Dabei können sie, wie oben erwähnt, an ganz unterschiedlichen Stellen Schwierigkeiten haben, die in der nachfolgenden Darstellung aufgezeigt werden:

Ein zentrales Problemfeld ergibt sich oft schon daraus, das Problem überhaupt zu erfassen. Denn: Probleme, die nicht gesehen oder verstanden werden, können auch nicht gelöst werden. Die Fragen „Worum geht es in der Aufgabe eigentlich?“ und „Was will/ soll ich herausfinden?“ müssen Kinder sich stellen und beantworten können und sollte somit immer mit allen Kindern geklärt werden, bevor sie in den Bearbeitungsprozess starten können.
Vielen Kindern fällt es dann schwer, die gegebenen Informationen zu nutzen bzw. die passenden ausfindig zu machen. Zudem müssen sie Vorgehensweise entwickeln, Zusammenhänge entdecken und eventuell auch auf bereits Be- oder Erkanntes zurückgreifen und mit diesen in Beziehung setzen.
Um das Problem dann zu lösen kann ihnen ebenso der mathematische Zugang fehlen. Vorwissen kann nicht aktiviert, genutzt bzw. der neuen Situation angepasst werden.
Und selbst wenn die Kinder eine Lösung ermittelt haben, ist es notwendig, diese dann auch mit der Aufgabenstellung in Verbindung bringen zu können. Dabei fällt es den Kindern manchmal schwer, unrealistische Ergebnisse als solche zu erkennen. Fehlen zentrale Vorstellung zu Größenbereichen oder der Problemstellung an sich, bleiben Ergebnisse oft unreflektiert stehen.
Von Anfang an sollten unterschiedliche Unterstützungsmöglichkeiten als Strukturierungshilfen in diesem Prozess mit den Kindern erarbeitet bzw. von ihnen genutzt werden. Wichtig zu sagen ist, dass sich der Einsatz nicht auf die Kinder beschränken darf, die die aufgezeigten Schwierigkeiten zeigen. Vielmehr sollen alle Kinder davon profitieren, um ihre Problemlöseprozesse (weiter) zu systematisieren und auch im Verlauf diese für andere nachvollziehbar zu begründen und darzustellen. Somit sollen sie als zentraler Bestandteil des ganz normalen Unterrichtsstoffes angesehen werden.
!!!Wichtig zu sagen ist, dass Kinder nicht nur im Kontext von Problemlöseaufgaben, sondern immer wenn das entdecken, beschreiben und begründen gefordert wird, unterstützt werden sollten. Denn auch die Kompetenz des Argumentierens ist abhängig davon, inwiefern die Kinder Beziehungen und Strukturen entdecken und für Begründungen heranziehen!!!
Im Folgenden werden Unterstützungsmöglichkeiten dargestellt und erläutert. Dabei unterscheiden wir zwischen sogenannten ‚Forscher-Mitteln‘, ‚Forscher-Strategien‘ und ‚Forscher-Fragen‘, die eng miteinander verknüpft sind und sich gegenseitig im Lösungsprozess bedingen und stützen können.
Forschermittel
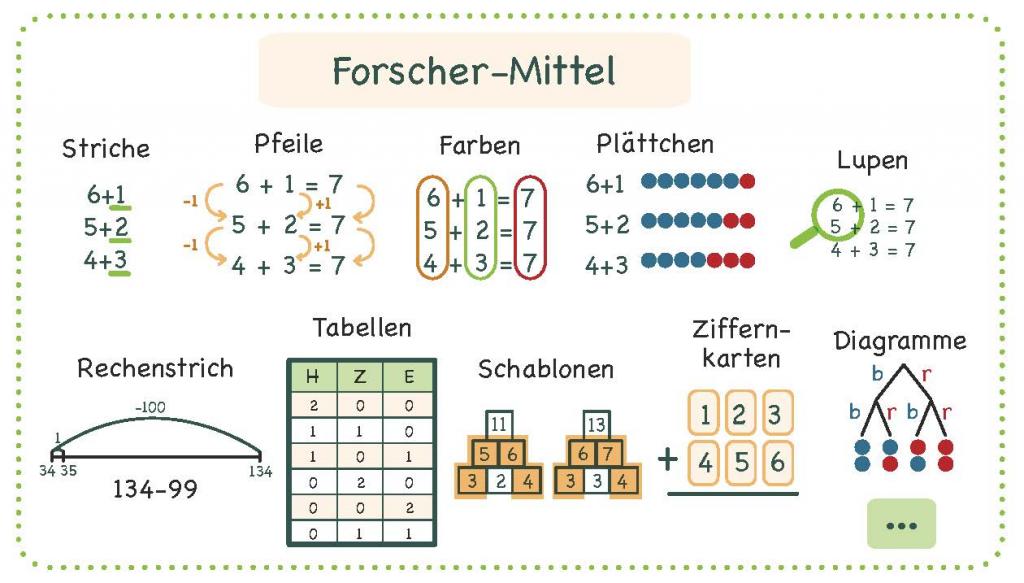 Die Abbildung ist ein Ausschnitt des Plakats „Das nutzen Mathe-Forscher“ von PIKAS (pikas.dzlm.de/node/556)
Die Abbildung ist ein Ausschnitt des Plakats „Das nutzen Mathe-Forscher“ von PIKAS (pikas.dzlm.de/node/556)
Forschermittel können helfen, eine Aufgabe so zu bearbeiten, dass sie leichter gelöst werden kann. Durch sie können relevante Zahlen o.ä. fokussiert in den Blick genommen oder in Beziehung gesetzt werden. Sie tragen dazu bei, das Problem zu verstehen aber auch zu strukturieren, seine Bearbeitung so zu unterstützen und die Ergebnisse auszudrücken.
Dabei unterscheiden wir u. a. zwischen folgenden „Forschermitteln'':
-
Farben
-
Pfeile
-
Plättchen
-
Lupen und Schblonen
-
Tabellen und Diagramme
-
Rechenstrich
Ihnen kommt dabei aber eine Doppelfunktion zu, denn sie dienen zum einen als Instrument (etwas markieren, um zu entdecken) des Lösungsprozesses, indem durch sie die Aufmerksamkeit zunächst auf Teilbereiche der Aufgabe gelenk werden kann, bis schließlich ein Gesamtzusammenhang erkannt wird. Zum anderen dienen sie als Dokument (markieren, um anderen erklären zu können) des Lösungsprozesses, da sie dort helfen können zu erklären, wo Worte fehlen (für sich und für andere) und bieten allgemein eine visuelle Unterstützung bei Begründungen.
Die wesentlichen Funktionen von Forschermitteln sind somit:
-
entdecken
-
hervorheben
-
strukturieren und ordnen
-
visualisieren
-
zueinander in Beziehung setzen
-
kommunizieren
Im dem Beispiel wird so durch die Umkreisung und Farben die Aufmerksamkeit auf die einzelnen Summanden gelenkt und fokussiert. So können deren Veränderung in den Blick genommen und zueinander in Beziehung gesetzt werden.
Auch andere können so erkennen, welche Entdeckungen gemacht wurden – eine gemeinsame Kommunikationsbasis entsteht.

Zudem muss den Kindern die Relevanz von Forschermitteln deutlich werden, indem im Unterricht über ihre Funktionen reflektiert wird. Eine solche Reflexion kann z.B. dadurch angeregt werden, dass mit den Kindern verschiedene „Forschermittel" auf einem Plakat gesammelt werden.
Forscherstrategien
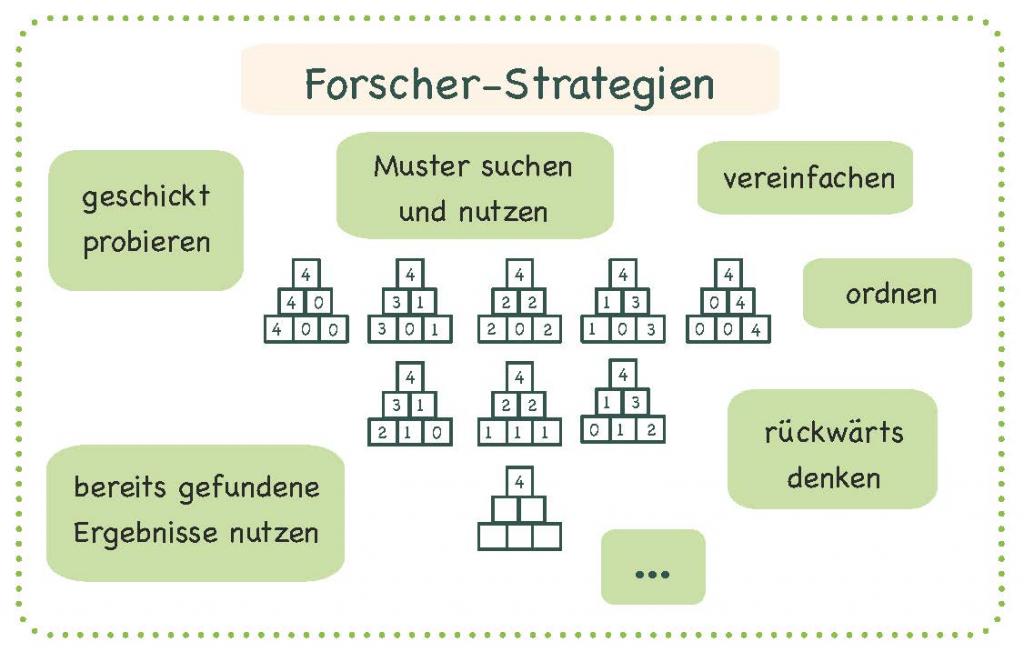
Der Ausgangspunkt vieler Kinder beim Lösen problemhaltiger Aufgaben ist oft ein eher unsystematisches Probieren. Nach dem „Versuch-Irrtum-Prinzip“ finden Kinder durchaus Lösungen für die Aufgaben, diese Vorgehensweise ist jedoch nicht effektiv und langfristig auch nicht erfolgreich. Deshalb sollen Kinder lernen, ihre Lösungsprozesse zunehmend systematischer zu gestalten, indem sie sich erkannte Beziehungen und Strukturen zunutze machen und flexibel denken.
 Die Abbildung ist ein Ausschnitt des Plakats „Das nutzen Mathe-Forscher“ von PIKAS (pikas.dzlm.de/node/556)
Die Abbildung ist ein Ausschnitt des Plakats „Das nutzen Mathe-Forscher“ von PIKAS (pikas.dzlm.de/node/556)
Forscherstrategien sind Tätigkeiten, die in einem Lösungsprozess als Hilfen zum Weiterdenken fungieren können. Der Einsatz von Forscherstrategien kann durch die Verwendung von Forschermitteln unterstützt werden, indem zunächst Auffälligkeiten und Strukturen verdeutlicht werden, um so Beziehungen zu erkennen, die für die Lösungsstrategie genutzt werden können.
Die wesentlichen Forscherstrategien für die Primarstufe sind...
-
geschicktes Probieren,
-
nachdenken und weiterarbeiten,
-
von hinten aus denken,
-
ordnen,
-
Muster suchen und
-
vereinfachen.
Um diese zu initiieren, sollten unterschiedliche Forscherstrategien an geeigneten Beispielen auch von der Lehrkraft vorgemacht werden bzw. darüber reflektiert werden (Was ist das Besondere an dieser Vorgehensweise? Was weiß ich/ muss ich wissen, damit ich so oder so vorgehen kann?). Zwar erfordern neue Aufgabenstellungen in unterschiedlichen Kontexten immer ein Anpassen dieser Strategien an den neuen mathematischen Sachverhalt, jedoch kann an den Beispielen das „Umdenken“ der Kinder angeregt werden.
Wichtig ist, diese Lösungsstrategien nicht als Lösungsrezepte anzusehen. Es muss eine für die Aufgabe passende Strategie ausgewählt bzw. adaptiert werden. Es sind ja keine starren Muster, sondern nur Leitideen, die man aber an die jeweilige Aufgabe anpassen muss.
Forscherfragen
 Die Abbildung ist ein Ausschnitt des Plakats „Das nutzen Mathe-Forscher“ von PIKAS (pikas.dzlm.de/node/556)
Die Abbildung ist ein Ausschnitt des Plakats „Das nutzen Mathe-Forscher“ von PIKAS (pikas.dzlm.de/node/556)
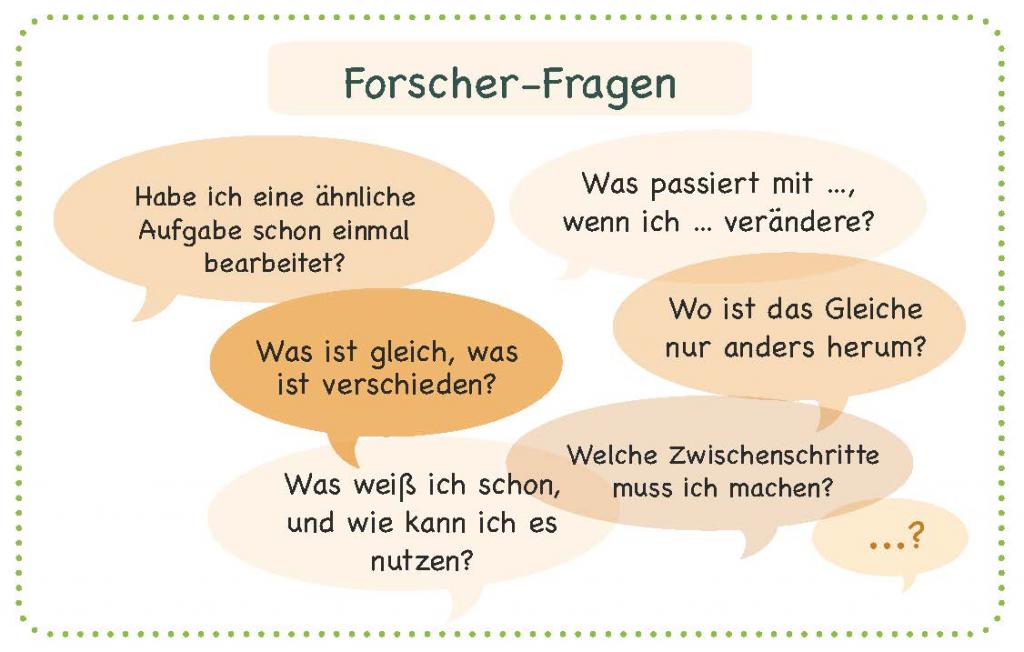
Forscherfragen sind Fragen, die als Hilfen zum Weiterdenken fungieren und die zur unterschiedlichen Forscherstrategien führen sollen. Auch der Einsatz von Forscherfragen kann durch die Verwendung von Forschermitteln unterstützt werden.
Die wesentlichen Forscherfragen für die Primarstufe sind folgende:
-
Habe ich eine ähnliche Aufgabe schon bearbeitet?
-
Wo ist das Gleiche anders herum?
-
Was ist gleich, was ist verschieden?
-
Was passiert mit ..., wenn ... ?
-
Aus welchen Teilen besteht die Aufgabe?
-
Was weiß ich alles schon, und wie kann ich das nutzen?
-
Was ändert sich, wenn ich ... auf ... übertrage?
Forscherfragen fokussieren sich also auf Zusammenhänge in bzw. zwischen Aufgaben (innerhalb der Lernumgebung oder strukturähnlichen Aufgabenstellungen – und nicht nur im arithmetischen Bereich). Durch diese sollen die Kinder sich die Aufgabe in ihren Zusammenhängen erschließen, sie auf Teilprobleme reduzieren oder aber gewisse (operative) Veränderungen zunächst selbst untersuchen.
Kinder sollen sensibel dafür werden, sich in Problemlöseprozessen diese Fragen zunehmend selbst zu stellen, um die daraus zu gewinnenden Erkenntnisse in die Beziehungen und Strukturen zur Ausbildung von Strategien zu nutzen.
Zusammenfassung
(Problem-)Lösen ist ein komplexer Prozess, in dem sich die Kinder zum einen stetig üben müssen und zum anderen Unterstützungsmaßnahmen benötigen, um ihn zu strukturieren und zu systematisieren. Sie sollen unterschiedliche Strategien kennenlernen und diese nutzen, dabei können Forschermittel und Forscherfragen helfen, sich die Aufgaben nicht nur zu erschließen, sondern systematisch Beziehungen und Strukturen zu untersuchen, zu entdecken und deren Nutzen für die Aufgabenlösung zu erkennen.
Das folgende Plakat kann mit allen Kindern gemeinsam besprochen und erarbeitet und dann sichtbar im Klasenraum aufgehängt werden (PIKAS: Unterrichtsmodul: Gute Aufgaben - Forschermittel).
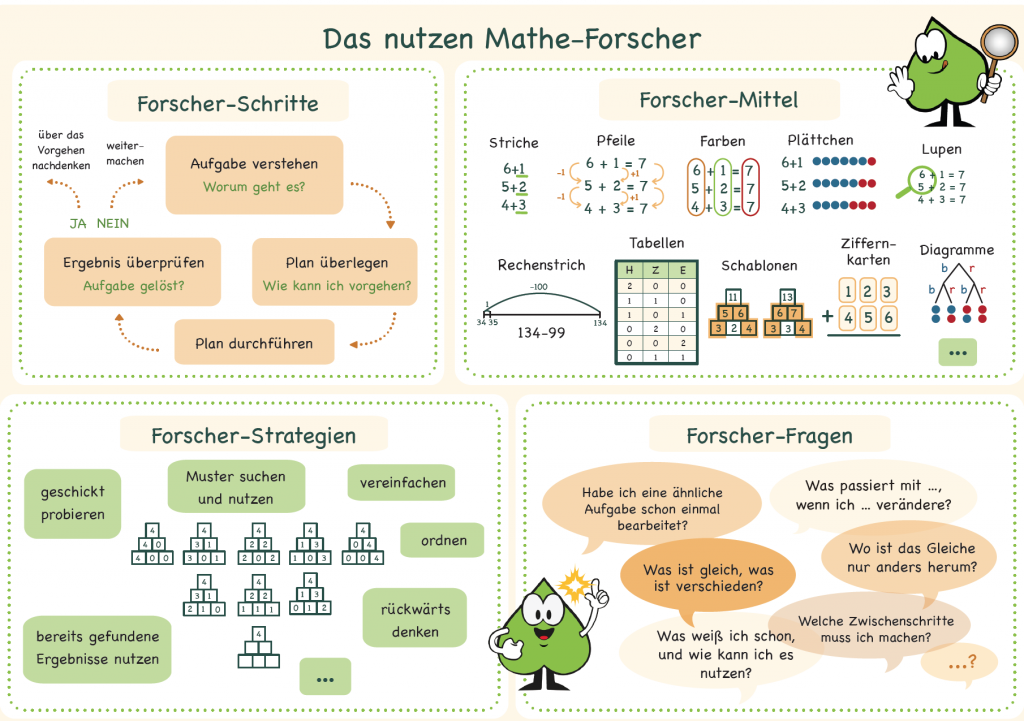 Plakat ,,Das nutzen Mathe-Forscher'' von PIKAS
Plakat ,,Das nutzen Mathe-Forscher'' von PIKAS
 Das entsprechende Informationspapier finden Sie hier (pikas.dzlm.de/node/556)
Das entsprechende Informationspapier finden Sie hier (pikas.dzlm.de/node/556)
Zu beachten ist:
-
Die Auflistung der Forscher-Mittel besitzt wie die der Forscher-Strategien und der der Forscher-Fragen keinen Anspruch auf Vollständigkeit und kann, je nach Aufgabenstellung und möglichem Lösungsweg, ergänzt werden.
-
Forschmittel & Co sind zum einen Lernhilfe, aber gleichzeitig auch Lernstoff, so dass ein zielführender Einsatz „gelernt“ werden muss.
-
Forschmittel & Co sind nicht nur als vorläufig zu verwenden ,Hilfsmittel’ kennenzulernen.
-
Im Unterricht muss angestrebt werden, einen natürlichen Einsatz und Umgang mit ihnen zu realisieren.
-
Vorab müssen Forschermittel & Co inhaltlich geklärt und die Kinder immer wieder dazu angeregt werden, diese zu verwenden, sowie stets über ihre Verwendung mit den Kindern auch zu sprechen.