Auf der folgenden Seite soll am Beispiel des Aufgabenformats „Zahlenmauern“ ganz konkret dargestellt werden, wie Forschermittel & Co die Kinder bei der Bearbeitung von Problemlöseaufgaben unterstützen können und wie sie im Unterricht eingebunden werden können.
Wie Sie der primakom-Seite „Zahlenmauern“ im Bereich „Aufgabenformate“ entnehmen können (Zahlenmauern – Einstieg), gibt es neben der bereits im Einstieg und Hintergrund aufgegriffenen problemorientierten Aufgabestellungen zur Ermittlung von Zahlenmauern zur vorgegebenen Zielzahl 4 vor allem auch operative strukturierte Aufgabenstellungen im Kontext der Zahlenmauern. In deren Auseinandersetzung können die Kinder zunächst vielfältige Entdeckungen machen, die sie darstellen und begründen sollen.
Dabei untersuchen die Kinder die Auswirkungen auf das Zahlgeflecht, wenn sich die Basissteine verändern (z.B. „Erhöhe den linken Basisstein um 1. Was passiert mit der Zielzahl? Warum ist das so?) und werden dabei durch Forscherfragen dazu angeregt, die zugrundeliegenden Strukturen und Zusammenhänge zwischen den Zahlen zu erkennen.
Dieses Wissen können sie dann nutzen, um zur Lösung weiterer (oder z.B. der Zielzahl-)Aufgabe systematische Lösungsstrategien zu entwickeln und dabei mit und durch Forschermittel Entdeckungen und Vorgehensweisen darzustellen.
Im Folgenden wird an ausgewählten Schülerdokumenten verdeutlicht, inwiefern die im Hintergrund dargestellten Unterstützungsmaßnahmen in dieser Lernumgebung eingesetzt und reflektiert werden können.
Forschermittel wie Pfeile, Farben oder Schablonen sollen den Entdeckungsprozess unterstützen, aber auch dazu genutzt werden, Auffälligkeiten darzustellen und zu begründen (Doppelfunktion als Instrument und Dokument, siehe Hintergrund). Das Markieren hilft vor allem in der Phase, in der die Kinder sich einen Plan zur Problemlösung machen, aber auch dann, wenn es darum geht, ihre Entdeckungen und Ergebnisse für andere sichtbar zu machen.
Hervorheben mit Schablonen
„Schau dir die Mauern an. Was fällt dir auf?''
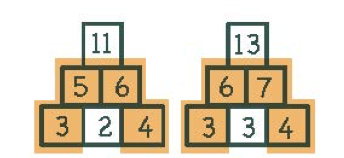
Um zum Beispiel die Auswirkungen operativer Veränderungen zu untersuchen (hier die Erhöhung des Decksteins um +2 bei einer Erhöhung des mittleren Basisstein um +1) können durch den Einsatz einer Schablone die zentral zu betrachtenden Objekten (hier der Basisstein und der Deckstein) fokussiert in den Blick genommen werden. Die Zusammenhänge bzw. die Auswirkung kann so schneller „abgelesen“ werden.
Mit Pfeilen (o.Ä.) Beziehungen darstellen
„Erhöhe den mittleren Basisstein um +2. Was fällt dir auf?“
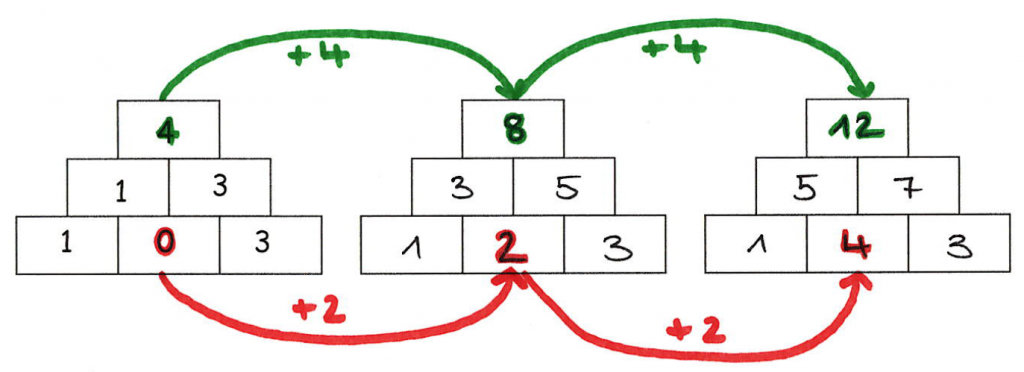
Durch den Einsatz bzw. das Markieren mit Farben und Pfeilen können einzelne Elemente oder Teilaufgaben in Beziehung gesetzt werden, um so Veränderungen zu verdeutlichen und Auswirkungen und Zusammenhänge zu fokussieren.
Im Beispiel kann die Auswirkung der operativen Veränderung des Basissteines (+2) auf den Deckstein (+4) dargestellt werden.
Entdecken
Zusammenhänge oder Muster können auch durch den Einsatz von Plättchen oder Farben gemacht und dargestellt werden.
So wird im Beispiel die Einwirkung der einzelnen Basissteine auf die Zielzahl durch die unterschiedlichen Plättchen veranschaulicht.
Dabei kann deutlich werden, dass die Erhöhung der äußeren Basissteine eine andere Einwirkung auf die Zielzahl hat als die Erhöhung des mittleren Basissteins.
Tipp: Schauen Sie sich zur Veranschaulichung auch den Hintergrund der primakom-Seite „Zahlenmauern“ an (Zahlenmauern – Hintergrund).
Der Einsatz von Forschermitteln sollte den Kindern an solchen geeigneten Beispielen von der Lehrkraft vorgemacht werden. Eine anschließende Reflexion („Wie hilft mir das Markieren?“; “Was kann ich mit den Pfeilen zeigen?“ etc.) soll den Kindern helfen, die Relevanz solcher Forschermittel auch für sich selbst zu entdecken, damit sie diese in Bearbeitungsprozessen nicht nur nach Aufforderung nutzen.
Problemlösen hat eine experimentelle Komponente und erfordert somit auch “Ausprobieren”. Wie im Hintergrund erwähnt, ist dies strategiegeleitet meist eher erfolgreich als nur nach dem „Versuch-Irrtum“ zu arbeiten.
So sollen die Kinder beim Lösen unterschiedlicher Problemstellungen (Untersuchen von operativen Veränderungen, Finden unterschiedlicher Zahlenmauern zu vorgegeben Zielzahlen) zunehmend systematisch vorgehen. Durch konkrete Anregungen und Fragestellungen können sie verschiedene Strategien entwickeln, die an geeigneten Beispielen von den Kindern oder aber auch von der Lehrkraft eingebacht werden sollen.
Geschicktes Probieren
,,Wie musst du den Basisstein verändern, damit der Deckstein um 1 größer wird?''
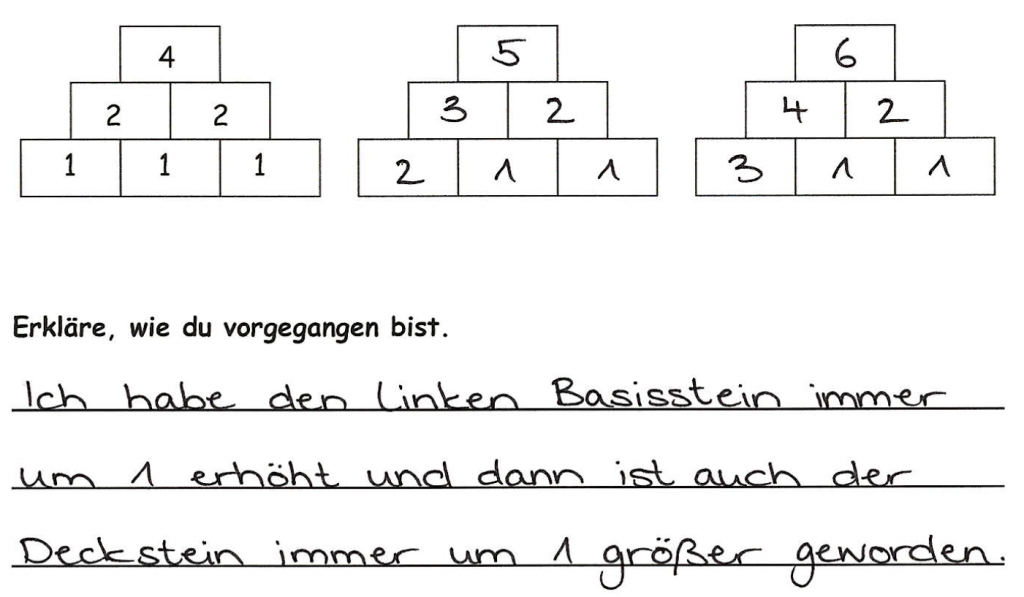
So können ausgehend von dem ersten Beispiel operative Veränderungen untersucht und vorgenommen werden, um Wirkungen hervorzusagen und diese Erkenntnisse dann zunehmend systematisch zu nutzen.
In dem die Kinder durch geschicktes, und somit systematisches probieren Auswirkungen untersuchen und verstehen, können sie sich diese Einsichten in anderen Problemstellungen zunutze machen und zielgerichteter selbst Veränderungen vornehmen, um etwa Zahlenmauern mit anderen Zielzahlen zu finden.
Von hinten aus denken
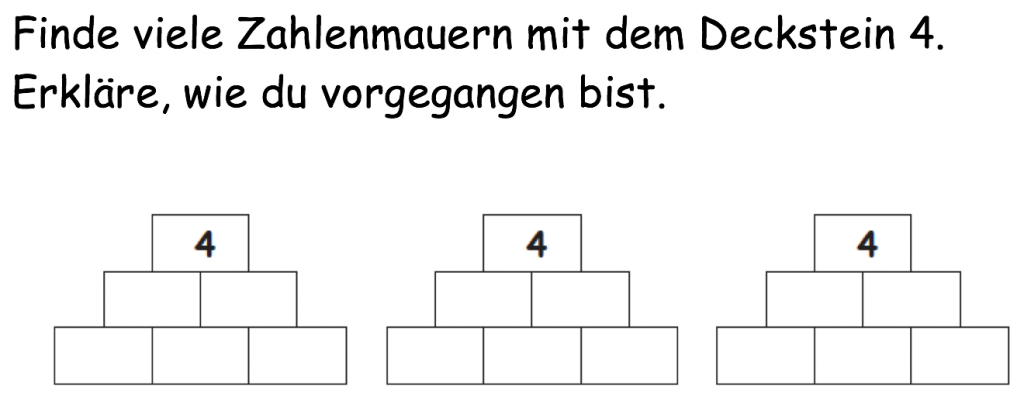
,,Wie kannst du geschickt Zahlenmauern mit der Zielzahl 4 finden?''
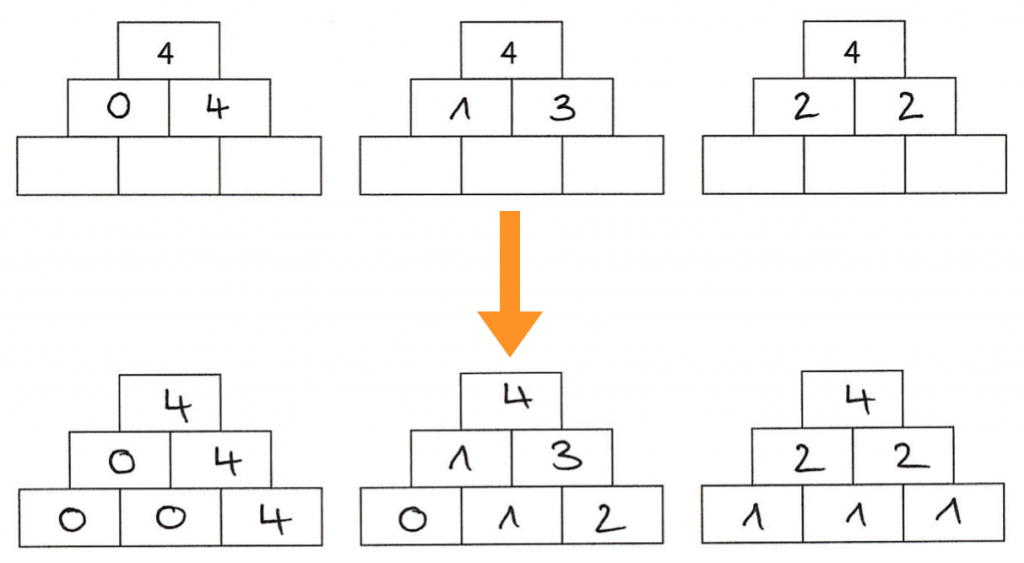
Beim Rückwärtsarbeiten beginnt man am Ende und arbeitet sich ausgehend vom Gesuchten „nach vorne“ – also rückwärts zum Gegebenen bzw. zum Bekannten durch. Man überlegt, wie die gewünschte Situation erreicht werden kann.
Hier wird die Struktur der Zahlenmauer genutzt, dass der Deckstein sich aus der Addition der Mittelsteine ergibt und so auch von oben nach unten gerechnet werden kann.
Vereinfachen
,,Schaue dir zunächst nur den oberen Teil der Zahlenmauer an. Wie viele Möglichkeiten kannst du finden?''
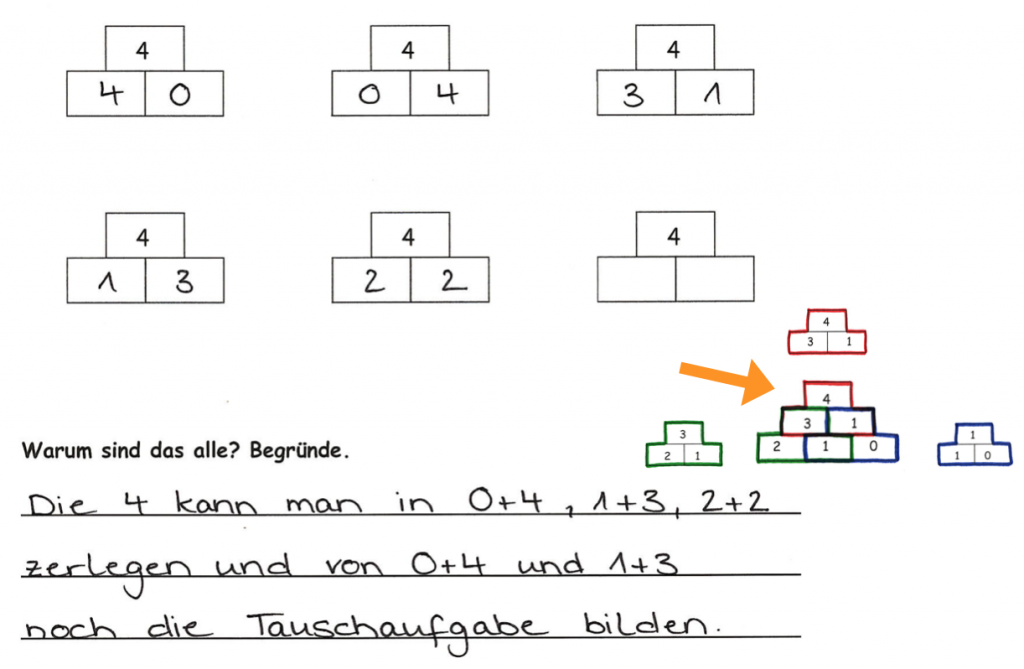
Das Ausgangsproblem kann zunächst auf ein Teilproblem reduziert werden. Dabei muss die Aufgabe sinnvoll zerlegt werden, um so die Problemstellung zunächst auf einer vereinfachten Ebene zu lösen.
In Bezug auf das „Rückwärtsarbeiten“ können die Kinder somit zunächst alle Möglichkeiten finden, den Deckstein mit den beiden Mittelsteinen zu erreichen und dann genau so weiter fortfahren, um die Basissteine zu ermitteln.
Ordnen
,,Welche Lösungen hast du gefunden? Sind das alle? Ordne.''
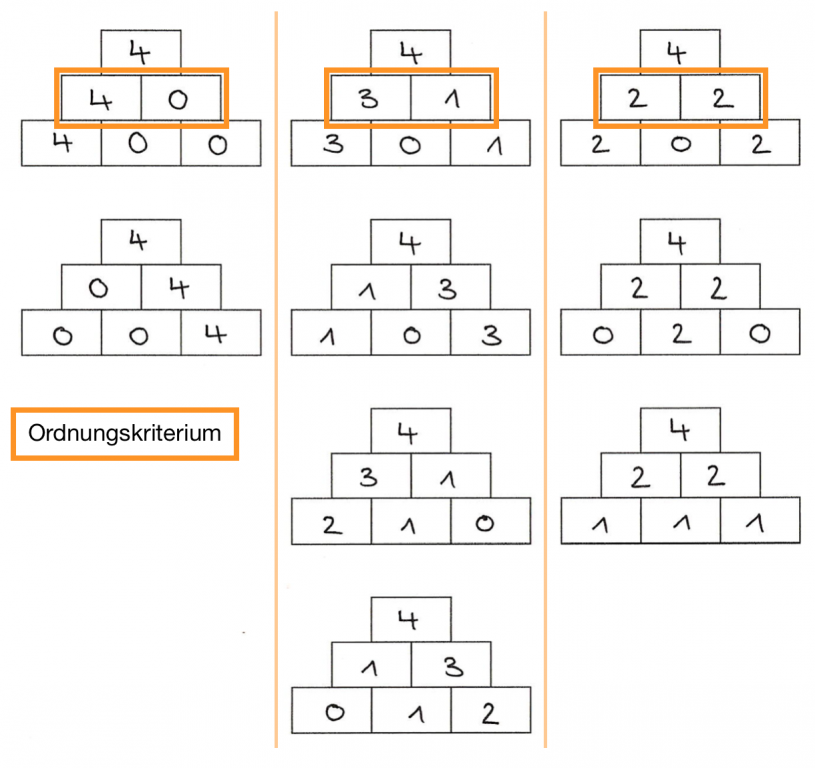
Können in einem Problemkontext viele unterschiedliche Lösungen gefunden werden und sollen die Kinder z.B. Vollständniskeiten begründen, sollten sie lernen, Lösungen zu strukturieren, also nach Kriterien zu ordnen.
So können zum einen Gemeinsamkeiten und Unterschiede zwischen den Lösungen entdeckt werden.
Zum anderen lässt sich eine Vollständigkeit so systemisch prüfen und begründen (Warum kann es keine andere Lösung mit der Zerlegung 4-0/3-1/2-2 als Mittelsteine geben?).
Forscherfragen sind Fragen, die als Hilfen zum Weiterdenken fungieren und damit auch zur Nutzung unterschiedlicher Forscherstrategien führen sollen, indem durch sie Beziehungen und Strukturen erkannt und genutzt werden können, um auch weiterführende Aufgabenstellungen zu lösen.
Analogieprinzip
„Was passiert mit dem Deckstein, wenn du nun den rechten Basisstein um +1 erhöhst?“
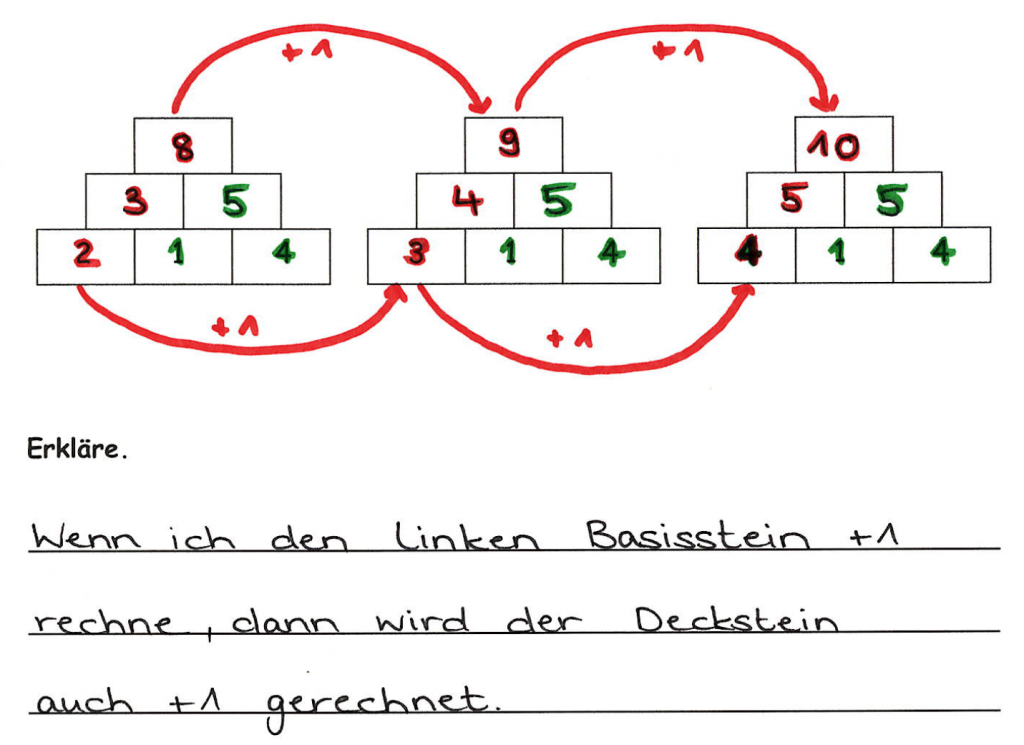
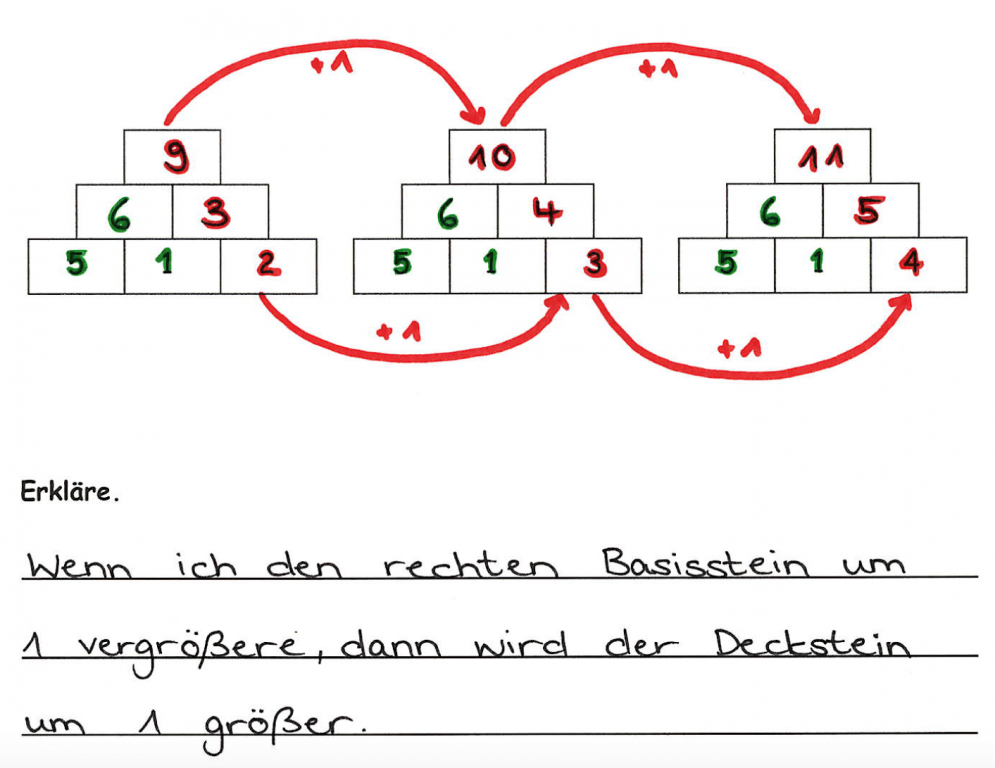
Analogien erlauben oft eine glaubwürdige „Vorhersage“ der Lösung „verwandter“ Aufgaben. Im Beispiel soll die Einsicht der operativen Veränderung des linken Basissteines den Kindern ermöglichen, eine Vorhersage zu treffen, was passiert, wenn nun der rechte Basisstein erhöht wird.
Aber: Manchmal kann die Lösung der analogen Aufgabe nicht sofort für die neue Aufgabe verwendet werden. Sie muss oft erst noch modifiziert und abgeändert werden. So müssen Kinder z.B. selbst entdecken, dass die Erhöhung des mittleren Basissteins die Zielzahl nicht analog verändert, da der Basisstein doppelt in diese eingeht.
Extremalprinzip
„Was passiert mit..., wenn...?“
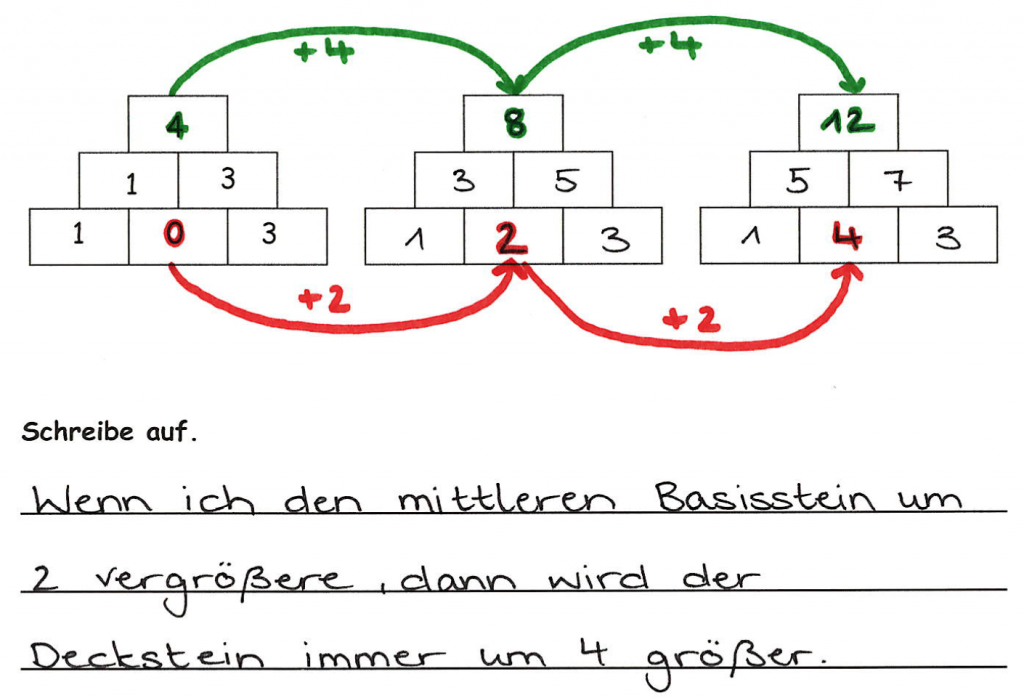
Um den Fokus auf operative Veränderungen und ihre Auswirkungen zu legen, sollen Lernende diese selbst ausführen.
Dabei kann eine konkrete Frage „Was passiert mit dem Deckstein, wenn ich den mittleren Basisstein um 2 vergrößere“ den Fokus auf die zu beobachtende Elemente setzen. Die Erkenntnisse daraus können dann genutzt werden, um weitere Zusammenhänge zu untersuchen oder zu antizipieren.
Transformationsprinzip
„Was ändert sich, wenn ich.... auf .... übertrage?“
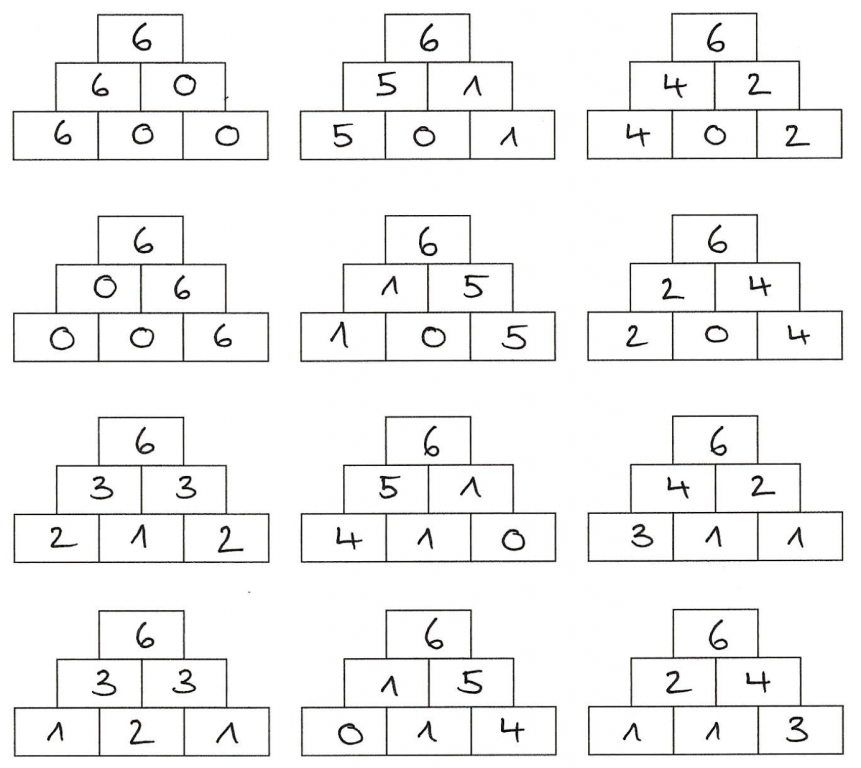
Bereits gewonnen Einsichten in Beziehungen und Strukturen sollen es ermöglichen, Zusammenhänge auch in komplexeren Problemstellungen (wieder) zuerkennen und diese Erkenntnisse zu nutzen und zu variieren.
Im Beispiel links bedeutet dies z.B. auch, Strategien zur Lösungsfindung der Zielzahlaufgabe 4 auf die neue Problemstellung zu übertragen, indem nun alle möglichen Zahlzerlegungen der 6 ermittelt werden. Auch kann hier „von hinten aus gedacht“ und das Problem zunächst zerlegt werden.
So kann die komplexere Problemstellung (mehr Lösungen) systematisch angegangen werden.
Neben diesen Unterstützungsmöglichkeiten sollen immer auch Sprachliche Hilfen (Sprachmittel) es den Schülerinnen und Schülern ermöglichen, Problemstellungen zu verstehen, zu bearbeiten und über das Denken und Vorgehen zu kommunizieren. Sprachbildung umfasst dabei sowohl die sprachsensible Unterrichtsgestaltung (Mikro-Scaffolding) als auch die gezielte Sprachförderung (Makro-Scaffolding) (siehe auch Vielfalt – Sprachförderung – Unterricht).
Die wesentlichen Sprachmittel sind:
