Hintergrund

Überschlagsrechnen - mehr als Rechnen mit gerundeten Zahlen

Was ist Überschlagsrechnen und warum ist es wichtig?

Insbesondere im Alltag ist genaues Rechnen nicht immer möglich, nötig oder sinnvoll. Wenn es schnell gehen muss (z.B. im Supermarkt an der Kassenschlange) oder eine genaue Rechnung im Kopf zu kompliziert wird, reicht eine ungefähre Rechnung meist aus. Gerade im Zeitalter der neuen Medien ist es außerdem wichtig, mit dem Taschenrechner oder Handy gewonnene Rechenergebnisse auf ihre Richtigkeit hin zu überprüfen, da sich hier leicht Tippfehler einschleichen können.

Da das Überschlagsrechnen im Unterricht aber häufig als reines Rechenverfahren eingeführt wird, ist Kindern die Bedeutung und die Alltagsrelevanz jedoch selten bewusst. Aussagen wie die von Tim im Eingangsbeispiel deuten darauf hin, dass er das Überschlagsrechnen nur als ein Rechenverfahren kennengelernt hat, dass er dann anwendet, wenn es von ihm (in der Schule) verlangt wird.

Das obige Beispiel gibt eine erste Antwort auf die Ausgangsfrage, warum das Überschlagsrechnen wichtig ist. So ist die Berechnung von Rabatten eine typische Alltagssituation, in der wir bewusst oder auch unbewusst Überschlagsrechnungen durchführen. Im Folgenden soll dies weiter ausgeschärft und die Bedeutung des Überschlagsrechnens geklärt werden.

Zunächst wird dazu das Überschlagsrechnen vom sogenannten Schätzen abgegrenzt. Auch wenn diese Begriffe häufig synonym gebraucht werden, so wird hier übereinstimmend mit Lorenz (2005) das Überschlagsrechnen als eine Rechnung verstanden, bei der es gilt, „das Ergebnis einer arithmetischen Operation ungefähr, das heißt, mit einer gewissen Näherung, aber damit durchaus auch mit einem einkalkulierten Fehler zu bestimmen“ (Lorenz 2005, S. 44).

Im Gegensatz zum Schätzen sind dabei alle notwendigen Zahlen bekannt und es wird bewusst oder unbewusst auf eine genaue Rechnung verzichtet – wie im obigen Beispiel der Rabattaktion. Ziel des Überschlagsrechnens ist daher die Vereinfachung einer Aufgabe, damit die Rechnung schnell und einfach im Kopf zu lösen ist.

Das Schätzen zeichnet sich hingegen dadurch aus, dass bestimmte Zahlenwerte unbekannt und daher abgeschätzt werden muss: Wie viele Minuten brauche ich ungefähr für eine Strecke von 2 km? Wie viel Liter Milch trinkt eine fünfköpfige Familie pro Tag? Zur Beantwortung solcher Schätzfragen, muss für einzelne Werte erst eine Annahme getroffen werden, bevor gerechnet werden kann, wie es z.B. bei den sogenannten Fermi-Aufgaben häufig der Fall ist (KIRA: Größen und Messen – Bauernhofaufgaben).

Welche Möglichkeiten gibt es einen Überschlag sinnvoll und nicht nach einer vorgegebenen Regel durchzuführen?

In der Tat ist die Anwendung der konventionellen Rundungsregeln (ab 5 aufrunden bis 4 abrunden) eine mögliche Strategie, einen Überschlag durchzuführen. Daneben gibt es jedoch viele weitere Strategien, die im Mathematikunterricht alle als korrekt angesehen werden müssen und die je nach Aufgabe gewisse Vorteile gegenüber dem Runden haben. Wichtig ist es, dass die Kinder kernen, dass es nicht DEN Überschlag und auch nicht DIE Notationsweise für den Überschlag gibt. Im Folgenden werden die Hauptstrategien aufgeführt:

regelkonformes Runden

298 + 341 ≈

300 + 300 = 600
300 + 340 = 640

16,49 + 15,49

16,50 + 15,50 = 32
16 + 15 = 31

Kommentar

Runden mit den Rundungsregeln

geschicktes Runden

298 + 341 ≈

300 + 340 = 640
300 + 350 = 650
300 + 341 = 641

16,49 + 15,49

16 + 16 = 32 (hier: gegensinniges Verändern)

Kommentar

Es wird so gerundet, dass Rechenvorteile entstehen: Welche ähnliche Aufgabe kann ich leichter lösen als die Ursprungsaufgabe? (Beispiel 298 + 341).
Wie kann ich die Zahlen verändern, ohne dass ich zu weit vom genauen Ergebnis abweiche? (Beispiel 16,49 + 15,49)

Abbruchsverfahren

298 + 311

290 + 310 = 600

16,49 + 15,49

16 + 15 = 31

Kommentar

Rechnen nur mit den führenden Ziffern, kleinere Einheiten werden vernachlässigt („abgebrochen“) – z.B. abgedeckt oder durchgestrichen. 

Kompensation

298 + 341 ≈

300 + 350 = 650
Es wurde zweimal aufgerundet, somit muss das genaue Ergebnis unter 650 liegen, also ungefähr 640.

16,49 + 15,49 

16 + 15 = 31
Es wurde zweimal abgerundet, also liegt das genaue Ergebnis darüber, ungefähr bei 32.

Kommentar

Nach dem eigentlichen Überschlag wird die Abweichung zum genauen Ergebnis ausgeglichen, das Ergebnis somit „verfeinert“.

Weitere Beispiele und illustrierende Videos zu den Überschlagsstrategien finden Sie bei KIRA: Arithmetik – Überschlagsrechnen.

Darüber hinaus verwenden Kinder häufig auch individuelle Überschlagsstrategien, wie das folgende Beispiel von Jonas zeigt.

Eigenaktivität

Schauen Sie das Video und finden Sie heraus, wie Jonas diese Aufgabe überschlägt.

 

Kommentar zur Eigenaktivität

Jonas scheint das Ergebnis ab einer bestimmten Stelle im Lösungsprozess zu „sehen“. Er beginnt wie bei einer genauen Rechnung zu rechnen, bricht diese aber ab, denn „man kann das auch sehen“.

Andere Kinder mit ähnlichen Vorgehensweisen bringen Ausdrücke wie „und dann noch das Kleingedruckte“ oder „und noch ein bisschen mehr“ in ihre Argumentation mit ein. Damit haben diese Kinder bereits einen wichtigen Aspekt des Überschlagsrechnens verstanden: Bewusst oder unbewusst auf ein genaues Ergebnis zu verzichten. Eine Erkenntnis, die Kinder, die die Rundungsregeln perfekt anwenden können, nicht immer haben.

Vorgehensweisen wie die von Jonas, nennt man auch „informelle Überschlagsstrategien“. Sie sind besonders für sogenannte indirekte Überschlagsfragen wie „Reicht das Geld?“ oder „Ist das Ergebnis größer oder kleiner als...?“ geeignet, weil hier keine Zahl als Ergebnis benötigt wird.

Welche Aufgabentypen zum Überschlagsrechnung gibt es?

Beim Überschlagsrechnen gibt es verschiedene Aufgaben- bzw. Fragentypen. Häufig werden diese unsystematisch im Unterricht eingesetzt, es lohnt sich jedoch, sich der Unterschiede bewusst zu werden und diese im Unterricht aufzugreifen. In der nachstehenden Übersicht befinden sich vier verschiedene Aufgaben zum Überschlagsrechnen. Allen vier Aufgaben liegen die gleichen Zahlenwerte zugrunde. Dennoch ist die Zielsetzung jeweils eine andere und es ist von Vorteil diese Aufgaben mit unterschiedlichen Überschlagsstrategien zu lösen.

A
Mache den Überschlag:
276 + 68 ≈ 

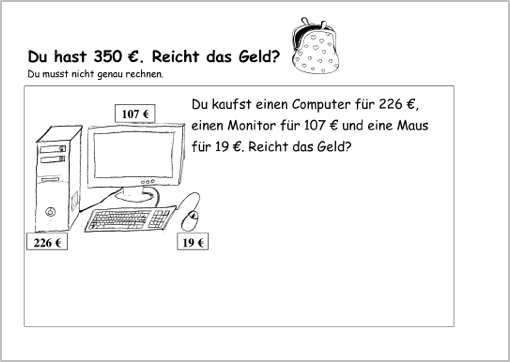
B
Du hast 350€. Du kaufst ein Fahrrad 276€ und einen Fahrradhelm für 68€.

• Das Geld reicht.
• Das Geld reicht nicht.

C
Du kaufst einen Computer für 276 € und ein Computerspiel für 68 €. Wie viel musst du ungefähr bezahlen?

D

Ist das Ergebnis größer oder kleiner als 350? Kreuze an, ohne genau zu rechnen:

• 276 + 68 < 350
• 276 + 68 > 350

Die Aufgaben A und C sind sogenannte direkte Überschlagsfragen (vgl. van den Heuvel-Panhuizen 2001) – hier ist jeweils eine Zahl als Ergebnis gefordert, so dass es zwingend notwendig ist, eine Überschlagsrechnung durchzuführen, z.B. durch Runden. Vielleicht haben Sie dazu 280 + 70 ≈ 350 gerechnet oder auch 300 + 70 = 370.

Besonders geschickt ist es bei diesem Beispiel gegensinnig zu runden: 280 + 60 = 340. Obwohl damit entgegen der Regeln gerundet wird, liegt der Überschlag näher am genauen Ergebnis (344) als die beiden anderen Rechenwege. Letztlich sind alle Rechenwege mit ihren jeweiligen Lösungen legitim, weil der jeweilige Kontext nicht weiter vorgibt, wie genau das Überschlagsergebnis sein muss.

Doch wie verhält es sich mit diesen Rechenwegen bei den Aufgaben B und D?
Bei diesen Aufgaben handelt es sich um sogenannte indirekte Überschlagsfragen (vgl. van den Heuvel-Panhuizen 2001) – dort ist keine Zahl als Ergebnis, sondern eine mathematisch begründete Entscheidung nötig. Löst man die Aufgabe durch Runden, so ist es besonders sinnvoll, beide Zahlen (unabhängig von den Rundungsregeln) aufzurunden. Denn so ist das Überschlagsergebnis in jedem Fall größer als das genaue Ergebnis.

Bei der Überschlagsrechnung 280 + 70 ≈ 350 kann man somit sicher sein, dass das Geld reichen muss bzw. dass das genaue Ergebnis < 350 ist. Hat man etwas großzügiger aufgerundet (300 + 70 = 370), muss man das Überschlagsergebnis noch „verfeinern“.

Besonders im Vergleich zu den Aufgaben A und C ist, dass man sich in beiden Fällen Gedanken zu den Auswirkungen der Vereinfachung, genauer des Rundens, machen muss. Hätte man einen Summanden auf- und den anderen Summanden abgerundet, wäre es recht knifflig, diese Auswirkungen rechnerisch zu bestimmen.

Unabhängig davon, wie Sie nun gerundet oder die Rechnung anderweitig vereinfacht haben – wichtig ist bei den indirekten Überschlagsfragen B und C zu erkennen, dass das Überschlagsergebnis hier nicht per se die Antwort auf die Fragestellung liefert, sondern noch interpretiert werden muss.