Stellenwerte: So funktionieren sie - manchmal aber auch nicht ...
Um die spezifischen Probleme und Hürden der Kinder bei der Entwicklung des Stellenwertverständnisses nachvollziehen zu können, ist es wichtig sich genau zu vergegenwärtigen, wie das Stellenwertsystem aufgebaut ist.
Wie ist unser Stellenwertsystem aufgebaut?
Fortgesetzte Bündelung
Das grundlegende Prinzip, das dem Stellenwertsystem zugrunde liegt, ist das Prinzip der fortgesetzten Bündelung (vgl. Padberg & Benz 2011). Dabei kann jede Menge durch fortgesetztes Bündeln eindeutig und schnell erkennbar dargestellt werden (vgl. Padberg & Benz 2011).
Dieses Prinzip bezieht sich auf die Bündelung einer realen Menge. Es werden immer Zehner-Bündel zusammengefasst, wobei a) solange weitergemacht wird, bis kein neues Bündel mehr voll wird, und b) werden fertige Bündel ihrerseits auch wieder zusammengefasst, wenn es mehr als zehn ihrer Sorte gibt. Aus Zehner-Bündeln entstehen auf diese Weise Hunderter-Bündel, aus diesen können Tausender-Bündel entstehen etc.
Diesem "Berg" Streichhölzer ist nicht auf den ersten Blick anzusehen, wie viele Streichhölzer es sind.
Ein erster Schritt diese unübersichtliche Menge zu strukturieren, ist das Zusammenfassen zu Zehnerbündeln (hier immer als Doppel-Fünf) - der erste Schritt zur fortgesetzten Bündelung. Bei einer so großen Anzahl von Streichhölzern bleibt jedoch die Zehnerbündelung immer noch unübersichtlich (hier ist nur ein kleiner Ausschnitt zu sehen). Daher kann weiter gebündelt werden.

Wenn, wie in diesem Beispiel, mehr als zehn Zehnerbündel entstehen, können diese wiederum zusammengefasst werden (der nächste Schritt der fortgesetzten Bündelung): In den Streichholzschachteln liegen jeweils zehn Zündhölzer; in den größeren Schachteln immer jeweils hundert (zehn Zehner) und im großen Würfel liegen tausend Zündhölzer (zehn Hunderter). Übrig bleiben zwei einzelne Zündhölzer: Das sind die Einer.
Jetzt kann man "sehen" wie viele Streichhölzer es sind: 40 + 300 + 1000 + 2.
Durch die fortgesetzte Bündelung entstehen auf diese Weise die Stellenwerte: 100, 101, 102, 103, ...
Die Gesamtanzahl der Objekte kann auf diese Weise nun sogar schon benannt werden. Entweder mit der konventionellen Sprechweise der Zahlen (Eintausend-dreihundert-zwei-und-vierzig) oder eher unkonventionell, jedoch genauso richtig: Ein Tausender und drei Hunderter und vier Zehner und zwei Einer oder Dreihundert-und-vierzig-und-zwei-und-tausend.
Notation von Zahlen
Nachdem die betreffende Menge durch Bündeln strukturiert wurde, kann man schnell erkennen um wie viele Streichhölzer es sich handelt. Will man jetzt schnell, eindeutig und ökonomisch (das meint vor allem: platzsparend zu schreiben und schnell zu lesen) aufschreiben, wie viele es sind, gelten zwei weitere Prinzipien: Das des Stellenwertes und das des Zahlenwertes (vgl. Padberg & Benz 2011).
Das Prinzip des Stellenwertes gibt vor, in welcher Reihenfolge die einzelnen Bündel angeordnet werden, nämlich indem rechts beginnend die Bündelungseinheiten nach links ansteigen.

Die Bündel werden zum eindeutigen Aufschreiben und Lesen immer in einer bestimmten Reihenfolge angeordnet: Die Einer werden ganz rechts hingelegt bzw. notiert, dann kommen links daneben die Zehnerbündel, links daneben die Hunderterbündel usw. Dies ist die Reihenfolge der Stellenwerte.
Das Prinzip des Zahlenwertes regelt, dass an der entsprechenden Stelle (also beim passenden Stellenwert) die Anzahl der jeweiligen Bündel notiert wird.
Jetzt kann die Zahl eindeutig aufgeschrieben werden: Die Anzahl der jeweiligen Bündel wird an der passenden Stelle notiert. Die passende Stelle ist durch die Reihenfolge der Stellenwerte festgelegt.
Diesen Übungen zum Sortieren der Bündel sollte genügend Zeit eingeräumt und sie sollten nicht zu früh abgesetzt werden, da sich durch diese Übungen ein "Bild" der Reihenfolge der Größe der Bündel bei den Kinder entwickeln kann.
An dieser Stelle empfiehlt es sich, bereits vorgefertigte Repräsentanten für Tausender, Hunderter, Zehner und Einer zur Verfügung zu stellen, die immer wieder genutzt und schnell bereit gestellt werden können - z. B. die Zehnersystemblöcke (vgl. Unterricht und Material →
Kartensatz 1 dient exemplarisch als Anregung zum Basteln eigener Übungskärtchen) (Bilder und Umsetzungsvorschläge aus Schulz 2015).
Was ist dann Stellenwertverständnis? Wie entwickelt sich das Stellenwertverständnis?
Stellenwerte "verstehen"
Von einer guten "Zahlvorstellung" können wir dann sprechen, wenn ein Kind (oder Erwachsener) in der Lage ist, sicher zwischen dem notierten Zahlzeichen einer Zahl, dem dazugehörigen Zahlwort und der entsprechenden (vorgestellten) Menge hin und her zu übersetzen.
Ein tragfähiges Stellenwertverständnis zeichnet sich insbesondere dadurch aus, dass das Kind weiß und erklären kann, wie die einzelnen Ziffern des Zahlzeichens, die Bestandteile des Zahlwortes und die Anzahlen der einzelnen Bündelungseinheiten zusammenhängen:
Die Vier steht links von der Drei, weil das die vier Zehner sind. Und die Zahl heißt Dreiundvierzig, weil sie aus drei Einern und vier Zehnern (also vierzig) zusammengesetzt ist (Abb. 7; vgl. auch Schulz 2014, S. 150).
 (in Anlehnung an Wartha & Schulz 2012)
(in Anlehnung an Wartha & Schulz 2012)
Welche typischen Probleme gibt es bei dieser Entwicklung
Mögliche Hürden und Anzeichen für Schwierigkeiten
Die Zahlwortbildung der zwei- (und mehrstelligen) Zahlen hat großen Einfluss auf die Entwicklung des Stellenwertverständnisses. Je regelmäßiger die Zahlwortbildung ist, desto unkomplizierter können Kinder (und Erwachsene) das System dahinter entdecken und verstehen. Die Zahlwortbildung im deutschen Sprachraum ist leider ziemlich unregelmäßig (vgl. Wartha & Schulz 2012).
Eine der auffälligsten Besonderheiten der Zahlwortbildung im Deutschen ist die sogenannte inverse Zahlwortbildung. Das heißt: Die Einer einer zweistelligen Zahl werden vor den Zehnern genannt. Das ist weltweit eine Ausnahme, die das Deutsche nur mit wenigen anderen Sprachen gemeinsam hat (z. B.: arabisch, niederländisch, madagassisch, flämisch) (vgl. Vannebo 2008).
Problematisch wird diese inverse Sprechweise vor allem beim Schreiben von Zahlen, weil die Anzahl der Stellenwerte in anderer Reihenfolge gesprochen als geschrieben werden (Beispiel: Vier-und-fünf-zig, aber 54). Dieses Problem vervielfacht sich bei mehrstelligen Zahlen (Beispiel: Drei-und-vier-zig-tausend-fünf-hundert-sieben-und-neun-zig, aber 43597).
Einige Kinder versuchen dieser "Gegenläufigkeit" zu entgehen, indem sie zweistellige Zahlen invers notieren; das heißt, sie notieren zuerst die Einer und dann die Anzahl der Zehner links davor - auf diese Weise wird zwar die "richtige" Zahl notiert, die inverse Schreibweise hat aber vor allem ein praktisches Problem, nämlich beim Eingeben von Zahlen in den Taschenrechner.
Hier müssen erst die Zehner und danach die Einer eingetippt werden, sonst erhält man einen Zahlendreher.
Eigenaktivität
Eine erste Hürde beim Lesen und Schreiben von mehrstelligen Zahlen ergibt sich, wenn der Schritt vom konkreten Material hin zur symbolischen Notation (1342) zu schnell erfolgt (vgl. das Beispiel mit den Zündhölzern). Das liegt am Abstraktionsgrad der geschriebenen Zahl und den strengen Konventionen, die hier eingehalten werden müssen, aber auch an den Regeln der Zahlwortbildung, die auch nicht "selbsterklärend" sind (vgl. Schulz 2014):
So wurden Kindern unterschiedliche Zahlen mündlich, also als Zahlwort, diktiert. Ihre Aufgabe war es, die diktierte Zahl in Ziffern zu notieren.
Welche Überlegungen führen wohl zu den von den Kindern aufgeschriebenen Zahlen?

Das letzte Beispiel im Kasten illustriert eines der wichtigsten Anzeichen für ein noch unsicheres Stellenwertverständnis: Zahlendreher (vgl. Warhta & Schulz 2012). Zahlendreher können bei allen "Übersetzungen" des oben vorgestellten Modells vorkommen - aufgedeckt werden können sie meist nur, wenn am Material geklärt wird, welche Anzahl überhaupt gemeint ist (vgl. Wartha & Schulz 2012).
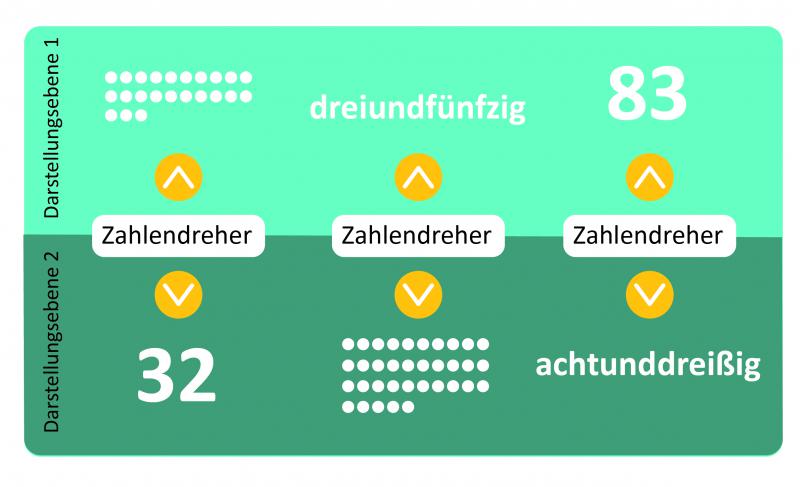
Die rein sprachliche Klärung, ob es sich bei der 43 um eine Dreiundvierzig oder eine Vierunddreißig handelt, oder ob Zweiundfünfzig nun so "25" oder so "52" geschrieben wird, bleibt in den meisten Fällen erfolglos. Das liegt vor allem daran, dass es sich ja auch bei den gesprochenen Zahlwörtern um "symbolische" Darstellungen handelt. Erst die Bezugnahme zur entsprechenden Menge kann eine Vorstellung zum Zahlwort, dem Zahlzeichen und den beteiligten Stellenwerten unterstützen.
Wie nun genau ein tragfähiges Stellenwertverständnis erarbeitet und gefestigt werden kann, wird auf der Unterseite "Unterricht" näher erläutert.
Diese Seite wurde erstellt von Axel Schulz für das primakom-Team.