Stellenwerte lesen, schreiben, verstehen
Im Hintergrund wurde skizziert, wie ein erster Zugang zum Stellenwertverständnis gestaltet werden kann - nämlich über die fortgesetzte Bündelung einer unübersichtlichen Menge gleichförmiger Objekte.
Im Folgenden soll geklärt werden, welche weiteren Aktivitäten zur Festigung des Stellenwertverständnisses und Reflexion des Stellenwertsystems erfolgen können. Dabei wird diesen eingangs gestellten Fragen nachgegangen:
Welche didaktischen Materialien sind zu diesem Zweck besonders geeignet?
Welches Material hilft mir und den Kindern? Und welches vielleicht nicht...
Wie immer bei der Auswahl eines "angemessenen" Arbeitsmittels für den Mathematikunterricht muss auch hier die Frage gestellt werden: Mit welchem Material kann der mathematische Inhalt gut "sicht- und handhabbar" gemacht werden? In diesem Fall also: Mit welchem Material können die grundlegenden Ideen des Stellenwertsystems "sicht- und handhabbar" gemacht werden?
Sowohl das Prinzip der fortgesetzten Bündelung als auch das Prinzip der stellengerechten Anordnung der Stellenwerte kann gut mit den Zehnersystemblöcken veranschaulicht, thematisiert und reflektiert werden (vgl. Scherer & Moser Opitz 2010; Wartha & Schulz 2012).

-
Die einzelnen Elemente des Materials sind bereits in Zehnerpotenzen strukturiert: Einerwürfel, Zehnerstangen, Hunderterplatten, Tausenderwürfel (analog ist auch das goldene Perlenmaterial von Montessori strukturiert).
-
Die Bündelungseinheiten können in ihrer stellengerechten Anordnung sortiert werden: Einer ganz rechts, Zehner links daneben, links daneben die Hunderter, etc.
Die erste Erarbeitung der Bündelungsidee sollte jedoch explizit nicht mit diesem vorstrukturierten Material erfolgen: Die Bündelungsidee und ihre Vorteile können mit diesem Material nur schwer selbstständig entdeckt und erarbeitet werden, weil sie ja bereits vorgegeben ist (stattdessen empfiehlt sich die Entdeckung der Bündelungsidee wie im
Hintergrund beschrieben).
Auch die zu schnelle Thematisierung der konventionellen Anordnung der Stellenwerte kann kontraproduktiv sein:
Die Notwendigkeit einer einheitlichen Sortierung würde auf diese Weise zu wenig reflektiert (vgl. Gaidoschik 2003, 2008; Schulz 2014). Stattdessen können Mengen auch immer mal wieder "unkonventionell" angeordnet dargestellt werden.

Eigenaktivität
Überlegen Sie selbst, warum der Zahlenstrahl, die Hundertertafel oder der Hunderterrechenrahmen sich zur Thematisierung der Stellenwerte nicht gut eignen würden.
Welche Unterstützungsmaßnahmen können wann im Unterricht eingesetzt werden?
Und nun...? Übungsformen und Reflexionsanlässe
Die Unterrichtsaktivitäten, Übungen und Reflexionsanlässe sollten einerseits das Verständnis der grundlegenden Prinzipien des Stellenwertsystems fördern und fordern, andererseits sollten sie mögliche "Stolpersteine" beim Verstehen der Stellenwerte besonders berücksichtigen.
Reflexionsanlass zu nicht vollständig gebündelten Mengen
Eine gute Möglichkeit die fortgesetzte Bündelung und deren Nutzen für die schnelle und konventionelle Notation von Zahlen zu festigen und zu reflektieren, bieten Gesprächsanlässe über nicht vollständig gebündelte Mengen - denn erst diese machen ein Nachdenken über den Sinn der Bündelung und das Schreiben von Zahlen notwendig. Wenn immer schon alles "schön" gebündelt ist, würde dieser wichtige Reflexionsanlass sich gar nicht ergeben.


Ungebündelte Anzahl an Einern - Wie soll das jetzt aufgeschrieben werden?
Eigenaktivität

Peter hat seine Streichhölzer gebündelt und sagt dir: "Ich habe zwei Hunderter, dreizehn Zehner und elf Einer. Wie wird die Zahl denn jetzt aufgeschrieben?"
Kannst du die Zahl jetzt gut aufschreiben? Kannst du Peter einen Tipp geben, der ihm hilft, die Zahl aufzuschreiben?
Überlegen Sie erst selbst, welche Tipps mit den Kindern gemeinsam erarbeitet werden können, wie man mit nicht vollständig gebündelten Mengen umgehen kann.
Die Thematisierung der Bestandteile der Zahlwörter
In regelmäßigen Abständen und kontinuierlich sollten im Unterricht die Bestandteile der Zahlwörter mehrstelliger Zahlen thematisiert werden.
Zahlendreher können auf diese Weise verhindert werden, wenn die Kinder bei der Zahl Dreiundvierzig nicht nur eine "Drei" und eine "Vier" hören (also den Klang des Zahlwortes nicht nur auf diese beiden beteiligten "Ziffern" reduzieren), sondern wenn sie die Bestandteile "Drei" und "Vierzig" hören und in ihrer Bedeutung für die Größe der Zahl einordnen können.
Hilfreich können hier Übungen sein, bei denen die Kinder zunächst einer gebündelten Menge (z. B. als Abbildung auf einer Karteikarte oder auch mit den Zehnersystemblöcken) die beteiligten Zahlwörter zuordnen - egal in welcher Reihenfolge und danach das "konventionelle" Zahlwort zuordnen: Zweitausenddreihundertfünfundvierzig.
Das Sortieren von Stellenwerten
Übungen zum Sortieren der Bündel (siehe Hintergrund) sollte genügend Zeit eingeräumt und sie sollten nicht zu früh abgesetzt werden, da die Kinder durch diese Übungen ein inneres Bild der Reihenfolge der Größe der Bündel entwickeln können. An dieser Stelle empfiehlt es sich, bereits vorgefertigte Repräsentanten für Tausender, Hunderter, Zehner und Einer zur Verfügung zu stellen, die immer wieder genutzt und schnell bereit gestellt werden können – z. B. die Zehnersystemblöcke.
Diese Übungen können mit Karteikarten in Partner- oder Gruppenarbeit gestaltet werden (vgl.
Material). Dabei kann auf eine stetige (und nicht zu schnelle Ablösung vom Material) geachtet werden (vgl. Schulz 2015).
"Holt euch die Zehnersystemblöcke und die Karteikarten: Ziehe eine Karte und ...
-
... sortiere selbst in der richtigen Reihenfolge und beschreibe deinem Partner, was du machst, um die Zehnersystemblöcke zu ordnen. Begründe auch wie du sortiert hast.
-
... beschreibe deinem Partner, wie er die Zehnersystemblöcke sortieren soll. Überlegt gemeinsam, ob die Sortierung passt.
-
... stellt einen Sichtschirm zwischen euch auf. Beschreibe deinem Partner, wie er die Zehnersystemblöcke sortieren soll, ohne dass du sehen kannst was er macht. Entfernt den Sichtschirm und überlegt gemeinsam, ob die Sortierung passt."
In jeder einzelnen Phase kann dann angegeben werden, wie viele Tausender, Hunderter, Zehner und Einer jeweils vorhanden sind: "Wir haben einen Tausender, drei Hunderter, vier Zehner und zwei Einer."

Das Sortieren von Stellenwerten und Schreiben von Zahlen
Zur Thematisierung unbesetzter Stellen und der Rolle der Null beim Schreiben von Zahlen eignet sich der Einsatz einer Stellenwerttafel. Diese ist deshalb so sinnvoll (und auch notwendig) da ein reines Sortieren der Bündel nur der Größe nach z. B. auch bei fehlenden Zehnern kein Problem wäre.
Erst das Sortieren der Bündel in eine Stellenwerttafel kann die Frage aufwerfen:
"Ich hab’ aber gar keine Zehner, was soll ich denn jetzt da hinlegen/hinschreiben?"
Die "Regel" zum Notieren von Zahlen lautet nun:
Wie viele Tausender, Hunderter, Zehner und Einer liegen jetzt dort in der richtigen Reihenfolge? Schreibe jeweils auf. Für fehlende Bündel, also eine leere Spalte der Stellenwerttafel, wird die Null notiert.
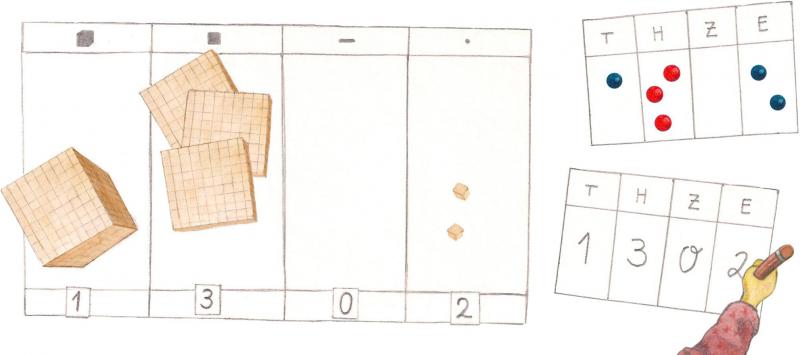
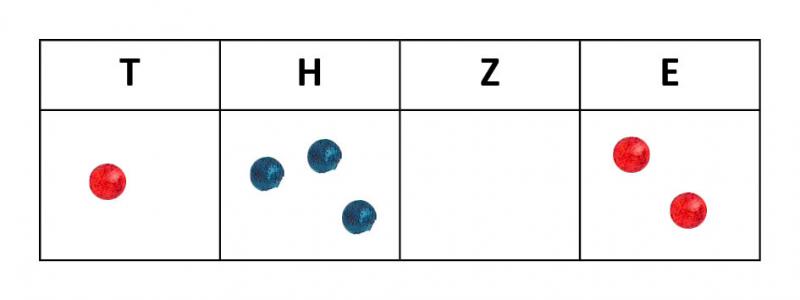
Wichtig dabei ist es zu wissen, dass die konventionelle Nutzung einer Stellenwerttafel nicht mit der Notation der Bündelgröße funktioniert (denn sonst würde die oben dargestellte Menge ja wie folgt notiert: 100030002, weil 1000 Tausender, 300 Hunderter, 0 Zehner und 2 Einer). Bei der konventionellen Nutzung der Stellenwerttafel wird die Anzahl der jeweiligen Bündel nur mit Plättchen (oder Punkten) repräsentiert.
In dem hier vorgestellten Beispiel jedoch soll zunächst noch die Nähe zur kardinalen Menge betont werden - die Kinder sollen noch "sehen können" wie viele es sind. Die vorgeschlagene Nutzung einer Stellenwerttafel bietet die didaktische Möglichkeit mit den Kindern über die Anzahl der jeweiligen Bündel zu sprechen: "Damit wir die Zahl gut aufschreiben können, müssen wir wissen, wie viele Bündel in den jeweiligen Spalten liegen - in unserem Beispiel also drei Hunderter und nicht dreihundert Hunderter. Wie viele Tausenderwürfel haben wir?" - "Einen."
Auch hier bieten sich Übungen in Partnerarbeit zur Verinnerlichung von Handlungen und zum Aufbau von Grundvorstellungen an. Der Fokus liegt nun auf dem Umgang mit unbesetzten Stellen und auf der Notation der Zahlen (Kartensatz 2 dient exemplarisch als Anregung zum Basteln eigener Übungskärtchen mit dem Fokus auf unbesetzten Stellen → Material).
"Holt euch die Zehnersystemblöcke und den Kartensatz 2: Ziehe eine Karte und ...
-
... sortiere selbst und beschreibe deinem Partner, was du machst, um die Zehnersystemblöcke zu ordnen. Notiert die Zahl. Begründe auch wie du sortiert und notiert Zahl hast.
-
... beschreibe deinem Partner, wie er die Zehnersystemblöcke ordnen und legen soll. Diktiere ihm die zu notierende Zahl. Überlegt gemeinsam, ob die Sortierung und Notation passt.
-
... stellt einen Sichtschirm zwischen euch auf. Beschreibe deinem Partner, wie er die Zehnersystemblöcke legen soll, ohne dass du sehen kannst was er macht. Diktiere ihm auch die zu notierende Zahl. Entfernt den Sichtschirm und überlegt gemeinsam, ob die Sortierung und Notation passt."
Die verständnisbasierte Notation von Zahlen ist der anspruchsvollste Schritt auf dem Weg zu einem guten Stellenwertverständnis. Bei der Notation von Zahlen steigt der Abstraktionsgrad enorm: Die Größe der jeweiligen Bündelungseinheit ist nicht mehr "sichtbar", sondern nur noch an der Position der Ziffer erkennbar. Bei der notierten Zahl 1342 weist allein die Position der 3 darauf hin, dass es sich hierbei um Hunderter handelt; stünde sie an anderer Stelle, würde sie etwas anderes bedeuten (vgl. Schulz 2015).
Die oben erwähnten Karteikarten sind im Bereich Material hinterlegt. Hier finden Sie zudem weiterführende praxisnahe Literatur und einen Link zu ausführlichen Fortbildungsfolien zum Thema "Stellenwertverständnis".
Diese Seite wurde erstellt von Axel Schulz für das primakom-Team.