Von der Hunderterkette zum leeren Zahlenstrahl
Der Übergang von der Hunderterkette zum Zahlenstrahl macht den Zusammenhang von Kardinalzahlen und Ordinalzahlen sichtbar. Auf dieser Basis können sich Lernende die dekadische Struktur des Zahlenstrahls, Beziehungen von Nachbarzahlen und somit Grundlagen des Rundens erwerben, z. B. welches ist der nächste Zehner zur 37? (vgl. Höhtker & Selter 1995).
Bei geeignetem Einsatz kann die Hunderterkette zudem ein passendes Arbeitsmittel zur Erweiterung des Zahlenraums bis 100 sein. Im Folgenden stellt sie als Perlenkette den Ausgangspunkt für die Unterrichtseinheit Von der Hunderterkette zum leeren Zahlenstrahl dar und dient somit als Basis für die Arbeit am Zahlenstrahl. Die Unterrichtseinheit beschreibt den Prozess vom konkreten Material zur abstrakten Vorstellung.
Die Perlenkette ist ein Material, das konkrete Handlungen zulässt. Sie eignet sich vor allem als zweifarbige Perlenkette. Alle Perlen sind nebeneinander auf eine Schnur aufgefädelt. Die Perlen sind als einzlene Elemente gut sichtbar und können leicht abgezählt werden. Somit kann an die bereits vorhandenen Kompetenzen der Kinder gut angeknüpft werden. Außerdem repräsentieren sie die Kardinalität der Zahlen. Einer einseitig ordinalen Zahlauffassung kann demnach vorgebeugt werden.
Später kann der Zahlenstrahl dann als Kette ohne Perlen leicht eingeführt werden.
Der Übergang von der Hunderterkette zum Zahlenstrahl ist in der vorliegenden Unterrichtseinheit in mehrere Schritte gegliedert.
1. Eigene Hunderterkette herstellen
Die Unterrichtsreihe beginnt mit der Herstellung eigener Hunderterketten. So stehen allen Kindern eigene Perlenketten zur Verfügung. Das Herstellen eigener Perlenketten ist nicht nur motivierend, sondern unterstützt außerdem durch die farbliche Trennung von je 10 Perlen die Verinnerlichung der dekadischen Struktur, die unserem Zahlsystem zugrunde liegt.
Hunderterkette:
Bei der Herstellung der Hunderterketten ist es wesentlich, mit den Kindern die zugrundeliegende Struktur zu erarbeiten. Dazu sollte eine große Hunderterkette als Demo-Material zur Verfügung stehen.
2. Orte finden
Die Einteilung an der Hunderterkette sollte mit den Kindern thematisiert werden. Für die Arbeit an der konkreten Hunderterkette sollte genügend Zeit eingeräumt werden. Wichtig ist, dass die Kinder den Aufbau der Kette verinnerlichen. Dabei sollte darauf geachtet werden, nicht zu früh zum nächstem Schritt überzugehen.
Eine Schwierigkeit ist die Tatsache, dass auf der Suche nach den Zahlen 41 - 49 im fünften Abschnitt gesucht werden muss. Dies widerspricht der Intuition und führt daher immer wieder zu Fehlern.
Folgende Zuordnungsübungen mit den Hunderterketten (konkret) können die Orientierung erleichtern:
-
Zahl finden: Orte an der Kette vorgegeben, Zahl muss benannt werden
-
Ort finden: Zahl wird vorgegeben, Ort an der Kette muss gefunden werden
Unterrichtspraktischer Hinweis
Aus der Unterrichtserfahrung heraus scheint es den Kindern leichter zu fallen, zu vorgegebenen Orten die entsprechenden Zahlen zuzuordnen. Daher sollten diese Aktivitäten zuerst durchgeführt werden.
Die Kinder können leere Kärtchen beschriften, die mit Wäscheklammern an der Hunderterkette befestigt wurden.
Umgekehrt können die Kinder selbst Karten beschriften und an die Kette hängen. Dabei können die Kinder den Schwierigkeitsgrad selbst wählen und variieren. Somit erhalten Sie ganz nebenbei einen Überblick über den Lernstand Ihrer Klasse.
Die Arbeit an der Hunderterkette ist grundlegend für die Erarbeitung der ikonischen Darstellung (nächster Unterrichtsschritt). Geben Sie den Kindern genügend Zeit sich im neuen aber noch konkreten Zahlenraum zu orientieren
Knackpunkt
Auf der Suche nach der 31. bis 39. Kugel muss im vierten Abschnitt nachgesehen werden. Häufig suchen die Kinder im dritten Abschnitt; da liegen aber die Zahlen 21 bis 29.
Da der Zehner der Zahlen von 31 bis 39 mit der Zahl 3 beginnt, sehen sich die Kinder dadruch veranlast, im dritten Abschnitt zu suchen.
3. Hunderterkette (ikonische Darstellung)
Analog zu der Arbeit an der konkreten Hunderterkette werden die Zuordnungsübungen ebenfalls an der ikonischen Repräsentation (Abb. 2) fortgesetzt. Dabei unterscheiden sich die Aufgaben von denen an der realen Hunderterkette nicht.
Folgende Schülerbeispiele aus einer Arbeitsphase zeigen die Kompetenzen der Kinder aber auch ihre Schwierigkeiten.
Eigenaktivität
Die Kinder wurden gebeten, selbst Orte an der ikonisch repräsentierten Kette zu suchen, die entsprechende Zahl zu identifizieren und dieses "Pärchen" darzustellen.
Welche Kompetenzen zeigen die Kinder bereits? Wo haben sie noch Schwierigkeiten?
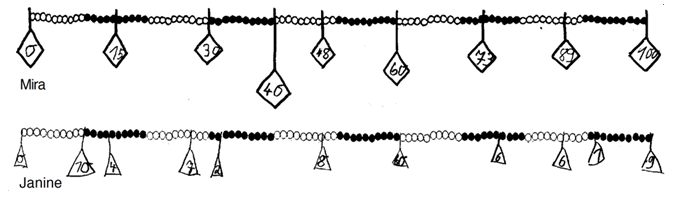(Höhtker & Selter 1995)
Die Schülerbeispiele zeigen wie wichtig das längere Verweilen in einzelnen Phasen ist, um sicher zu stellen, dass die Kinder tragfähige Vorstellungen aufbauen. Dabei ist es hilfreich über unterschiedliche Vorgehensweisen zu sprechen und diese zu thematisieren.
Fragen wie "Woher weißt du, dass dein Ergebnis richtig ist?" oder "Wie bist du auf dein Ergebnis gekommen?" helfen Kindern über ihre Vorgehensweisen nachzudenken und sich so auch dieser bewusst zu werden.
Orientierungshilfen besprechen
Ohne Orientierungshilfen, wie z. B. das Ausnutzen von Stützpunkten (glatte Zehner), ist es mühsam die Zahlen einzutragen, weil man auf das vollständige Auszählen angewiesen wäre.
Probieren Sie die Zahlen 12, 28, 34 auf folgender Kette einzutragen:
Fragen wie "Wie kannst du das herausfinden, wo eine Zahl liegt, ohne dabei zu zählen?" können den Kindern helfen, passende Strategien zu entwickeln. An dieser Stelle werden also schon Strategien vorbereitet, die für die Orientierung am leeren Zahlenstrahl hilfreich sein können.
Das Anordnen von Zahlenfolgen (z. B. 16, 26, 36, 46, ...) vertiefen die Einsicht in die Strukturgleichheit einzelner Zehner. Diese Übungen leisten einen wichtigen Beitrag zum tieferen Verständnis unseres dekadischen Zahlensystems.
Sie werden merken, dass die Kinder die reale Hunderterkette immer seltener benötigen, da sie im zunehmendem Maße mit der bildlich repräsentierten Hunderterkette und in der Vorstellung operieren.
Dazu passt:
Blitzrechenübungen an der Hunderterreihe (Zählen, Ergänzen zum Zehner).
4. Übergang von der Hunderterkette zum leeren Zahlenstrahl
Der Übergang in die nächste Phase darf nicht zu früh erfolgen, die Kinder sollten in der Lage sein, die Zuordungsübungen "Orte finden" und "Zahlen finden" an der ikonischen Hundekette ohne zur Hilfenahme der realen Kette zu lösen.
Als weitere Abstraktionsstufen wird der leere Zahlenstrahl eingeführt. Eine Kette ohne Perlen kann dabei als Anschauungshilfen dienen.
Die Übungen bleiben auch beim Zahlenstrahl wieder gleich: Orte finden und Zahlen finden.
Sinnvoll ist es, zunächst an beiden Anschauungsmitteln parallel zu arbeiten. Zum Einstieg sollten die Kinder z. B. vorgegebenen Orten der Hunderterkette die fehlenden Zahlen zuordnen und im zweiten Schritt auf den leeren Zahlenstrahl übertragen.
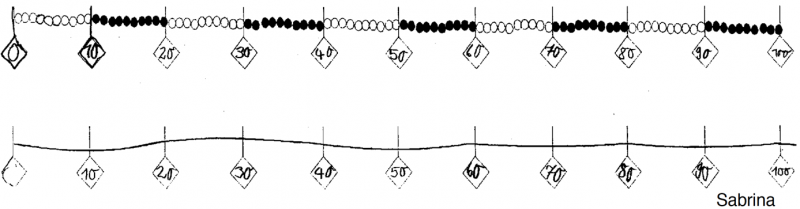
Knackpunkt beim Übergang zum Zahlenstrahl
Die erste Kugel ist die Eins. Der erste Strich auf dem Zahlenstrahl ist jedoch die Null. Wichtig ist, diesen Unterschied zwischen den Darstellungsmitteln zu thematisieren. Mit einem Forscherauftrag (Was ist gleich? Was ist verschieden?) lässt sich unter anderem dieser Knackpunkt herausarbeiten. Um den Brückenschlag von der Hunderterkette zum Zahlenstrahl zu machen, ist es wichtig, die Gemeinsamkeiten herauszustellen; gleichsam ist es notwendig die Unterschiede zu kennen, um möglichen Fehlerquellen vorzubeugen.
5. Zahlenstrahl ohne Hunderterkette mit Hilfszahlen
In der folgenden Phase kann der reale Zahlenstrahl ebenfalls eine Hilfe darstellen. Für diese Unterrichtphase gilt es, den Abstraktionsgrad sukzessive zu erhöhen. Dabei können folgende Aufgabenvariationen eine Orientierung geben:
a) Hilfszahlen vorgeben
b) weniger Hilfszahlen z. B. (0; 10; 50; 100) → (0; 50; 100) → (0; 100)
c) leerer Zahlenstrahl
Dabei können die reale Schnur (ohne Perlen) und die ikonische Repräsentation gegenübergestellt werden.
Die Strategien aus der dritten Unterrichtsphase können wieder aufgegriffen werden (z. B. Strategie: Mitte finden).
Knackpunkt:
Wichtig an dieser Stelle ist, dass alle Zahlen den gleichen Abstand haben. Zwischen zwei 10er-Zahlen liegen immer gleich viele Perlen. Das gleiche gilt für verschiedene 1x1-Reihen. Durch immer gleiche Aufgabenstellungen an der Hunderterkette zu Beginn der Reihe und am Zahlenstrahl können die Kinder die gelernten Strategien übertagen und somit zunehmend Sicherheit im Umgang mit dem Zahlenstrahl gewinnen.
Dabei ist es notwendig diesen Rückgriff auf vorherige Unterrichtsphasen zu thematisieren und den Kindern bewusst zu machen.
Wie hast du die Zahlen an der 100er Kette gefunden? Wie kannst du die Zahlen am Zahlenstrahl finden?
6. Zahlenstrahlintervalle
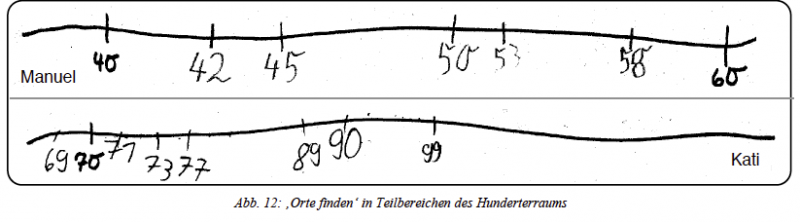
Hinweis: Dieses Anschauungsmaterial soll dazu auffordern, die ungefähren Orte für die entsprechenden Zahlen zu finden. Wichtig hierbei ist, die Relationen (ungefähr) darzustellen; eine exakte Positionierung der Zahlen ist nicht zentral.
Hinweis:
Nicht alle Kinder sind gleich, daher gilt es flexible Arbeitsphasen einzurichten. Auch, wenn die Unterrichseinheit wie eine Abarbeitung/ein Gleichschritt vorkommen mag. Je nachdem wie schnell sich Kinder von der realen, ikonischen Darstellung lösen können, ist die reale Hunderterkette als Stütze immer wieder denkbar; dies gilt auch für leistungsstarke Kinder.
Ein Strich zum Rechnen - Ein Ausschnitt aus dem Zahlenstrahl
Wie bereits im
Hintergrund erläutert, soll der Zahlenstrahl nicht zum Rechnen verwendet werden, da er zum Zählen in Einerschritten verleitet. Als Ausschnitt aus dem Zahlenstrahl kann der Rechenstrich jedoch eine geeignete Stütze, z. B. bei der Erarbeitung von Rechenstrategien, sein.
Der Rechenstrich ist ein ordnungstreues, aber nicht maßstabstreues Abbild des Zahlenstrahls. Der Übersichtlichkeit halber werden auf dem Rechenstrich nur Zahlen eingetragen, die zur Rechnung benötigt werden. Außerdem soll der Rechenstrich zum Rechnen verwendet werden, daher würde das Eintragen der genauen Abstände nur eine unnötige Belastung darstellen. Dabei reicht es aus, die Lage der Zahlen auf dem Rechenstrich nur ungefähr zu bestimmen (vgl. Müller & Wittmann 1994).
Zum Umgang mit dem Rechenstrich
