Der Zahlenstrahl - ein lineares Anschauungsmaterial
Ordinales Zahlverständnis beschränkt sich nicht nur auf das Kennen der Zahlwortreihe und dem Vorwärts- und Rückwärtszählen. Anschauungsmittel spielen eine bedeutende Rolle beim Mathematiklernen. Sie stellen eine Hilfe beim Vorstellungsaufbau der recht abstrakten Inhalte dar. Dabei sind sie ebenfalls Lerninhalte mit Knackpunkten und Stolpersteinen. Auf der folgenden Seite wird exemplarisch der Zahlenstrahl als lineares Anschauungsmaterial vorgestellt, mit dessen Hilfe ordinales Zahlverständnis aufgebaut werden kann.
Die Informationen sind wie folgt gegliedert:
Welche mathematische Idee steckt hinter dem Zahlenstrahl?
Der Zahlenstrahl gehört als zentrale mathematische Veranschaulichung zum Basisstoff der Grundschule. Als Anschauungsmittel verkörpert er besonders gut die fundamentale Idee der Zahlenreihe.
Mit der Idee des "immer eins weiter" repräsentiert der Zahlenstrahl die Unendlichkeit der natürlichen Zahlen (vgl. Klewitz et. al 2008, S. 24). Nachbarschaftsbeziehungen, insbesondere die Nachfolger- und Vorgängerrelation, werden besonders gut deutlich.
Der Zahlenstrahl ist, wie sein Name ausdrückt, ein Strahl mit einem Anfangspunkt und manchmal ohne Endpunkt, um zu verdeutlichen, dass die angeordnete Zahlenfolge prinzipiell fortgesetzt werden kann. Auf dem Strahl werden in normierten Abständen die Zahlen angeordnet. Die Fünfer- und Zehnerbündelung wird häufig mit dickeren Strichen optisch hervorgehoben. Maßstäbliche Verkleinerungen erlauben problemlos eine Erweiterung eines Zahlenstrahls auf alle Zahlenräume. Daber bleiben alle wesentlichen Strukturen erhalten (vgl. Käpnick 2014).
 Abb. 1
Abb. 1
Für Erwachsene mag diese Beschreibung einfach oder gar selbstverständliche klingen. Darin stecken aber eine Menge Details, auf die es ankommt und die von den Kindern verstanden werden müssen. Ein wichtiger Punkt dabei sind die normierten Abstände zwischen den Zahlen.
Lea wurde die Aufgabe gestellt, die Zahlen auf einem Zahlenstrahl einzutragen (Abb. 2). Auf den ersten Blick ist zu erkennen, dass ihr dies noch nicht gelingt. Sie zeigt noch große Schwierigkeiten beim Eintragen der Zahlen im Zahlenraum bis Zehn. Lea macht zwar schon viel richtig, trotzdem scheint sie die Relationen auf dem Zahlenstrahl noch nicht in den Blick zu nehmen. Sie hält die Reihenfolge der Zahlen korrekt ein und auch die Abstände zwischen den Zahlen sind (fast) gleich groß. Lediglich der Abstand zwischen der 9 und 10 ist zu groß.
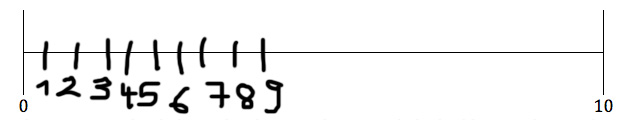 Abb. 2
Abb. 2
Bevor wir Lea helfen können, ihre Schwierigkeiten zu überwinden, sollten wir überlegen, welche Kompetenzen Lea benötigt, um die Aufgabe korrekt zu lösen. Mit der folgenden Eigenaktivität versetzen wir Sie für ein paar Minuten in die Lage eines Schulanfängers:
Eigenaktivität
Tragen Sie bitte folgende Zahlen am Zahlenstrahl ein:
3/4; 1/8

Traditionell werden Zahlenräume in der Grundschule sukzessive vom Zahlenraum bis 20 (1. Schuljahr), bis 100 (2. Schuljahr), bis 1000 (3. Schuljahr) und bis 1 Million (4. Schuljahr) erweitert. Als strenge Grenze sollten diese Zahlenräume jedoch nicht verstanden werden. Sie dienen als Orientierung und geben an, welche Zahlen im Schuljahr jeweils genau unter die Lupe geommen werden.
Wo immer sinnvoll und möglich, sollte der Zahlenraum nach oben (und unten) offen bleiben. Krauthausen und Scherer (2004) fordern, die Möglichkeiten der Erweiterbarkeit ausdrücklich in den Blick zu nehmen, „z. B. bei der Wahl von Arbeitsmitteln und Veranschaulichungen zur Zahldarstellung" (S. 6).
Diese prinzipielle Erweiterbarkeit denken wir jeweils mit, indem wir die erste höherstelligere Zahl als Orientierungsgrenze in den Zahlenraum einbeziehen, z. B. im Zahlenraum bis 100 mit 100 als einzige dreistellige Zahl. Damit ist der erste Schritt des "immer eins weiter" schon getan.
Welche Kompetenzen sind erforderlich, um sich auf dem Zahlenstrahl zu orientieren?
Die intuitiven Zahlvorstellungen der Kinder sind häufig durch lineare Vorstellungen beeinflusst. Man denke nur daran, dass Kinder bereits früh zu zählen beginnen und dabei den Mengenaspekt der Zahlen erst im Laufe der Zeit mit dem Zählprozess in Verbindung bringen (vgl. Zählprinzipien der Seite Zahlvorstellung erwerben).
Ordinale Zahlvorstellungen beinhalten die Vorstellungen einer Zahl als
-
Zählzahl (Folge der natürlichen Zahlen, die beim Zählen durchlaufen werden)
-
Ordnungszahl (Rangplatz in einer geordneten Reihe)
Die lineare Repräsentation der Zahlen am leeren Zahlenstrahl greift zwei Zahlaspekte auf. Zum einen geht es in einer ordinalen Vorstellung um den Ort und die Position einer Zahl in einer Reihe von Zahlen. Zum anderen können die Zahlen in Abstandsbeziehung zu anderen Zahlen vorgestellt werden. (Häsel-Weide & Nührenbörger 2012, S. 32)
Ordinales Zahlverständnis zeichnet sich also dadurch aus, dass die Kinder die Zahlwortreihe aufsagen können, dabei haben die Zahlen einen festen Rangplatz in einer Reihe. Obwohl der erste Zugang der Kinder zu Zahlen ordinal geprägt ist, fällt vielen Kindern die Orientierung auf dem Zahlenstrahl sehr schwer.
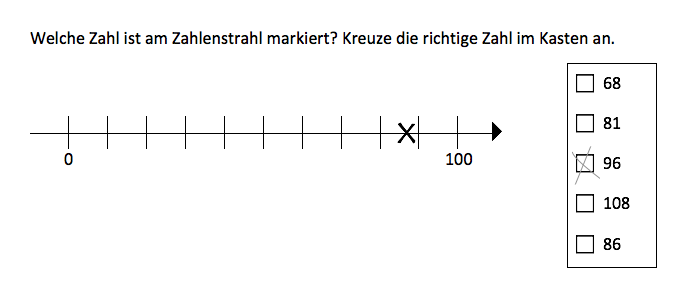
Denken Sie noch einmal an das Eingangsbeispiel. Sarah hat bereits ordinale Zahlvorstellungen erworben und kann sich grob auf dem Zahlenstrahl orientieren. Trotzdem gelingt ihr die korrekte Zuordnung nicht. Aus den vorgegebenen Zahlen hat Sarah die 96 der Markierung zugewiesen.
Um herauszufinden, welche Schwierigkeiten sie hat, ist es sinnvoll, sich zu überlegen, wie sie vorgegangen sein könnte.
Sarah weiß vermutlich, dass 96 nah bei 100 liegt. Vielleicht hat sie daher von 100 aus angefangen zu zählen.
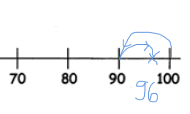
Das heißt natürlich nicht, dass die Kinder auf der Suche nach der 96 vorne zu zählen beginnen müssen, denn Abzählstrategien sind langwierig und fehleranfällig. Kinder sollten verschiedene Strategien anwenden können, um die Zahlen auf dem Zahlenstrahl zu finden (z. B. 96 ist um 4 weniger als 100; 90 ist um 10 weniger als 100, 90 + 6 ist 96). Bei der zweiten Strategie muss bei der Orientierung die Richtung gewechselt werden.
An dem Beispiel wird deultich, dass bei der Orientierung auf dem Zahlenstrahl das Wissen um erstens die Kardinalität der Zahlen und zweitens das Dezimalsystem notwendig ist. Ohne eine Vorstellung von weinger als und mehr als zu haben, fällt es schwer Positionen auf dem Zahlenstrahl zu verorten. Daher sollte die lineare Orientierung im Zahlenraum bis 100 erst dann erarbeitet werden, „wenn die Kinder bereits über ein grundlegendes Verständnis von Bündelungs- und Positionsprinzip verfügen" (Gaidoschik 2015, S. 168). (Siehe dazu Stellenwertverständnis)
Eigenaktivität
Jeweils vor und nach der Thematisierung des Zahlenstrahls hat die Lehrerin eine Standortbestimmung mit ihren Kindern durchgeführt.
Vergleichen Sie die beiden Standortbestimmungen.
Welche Kompetenzen hatte Frieda jeweils vor und nach der Behandlung im Unterricht? Welchen Lernfortschritt können Sie feststellen?
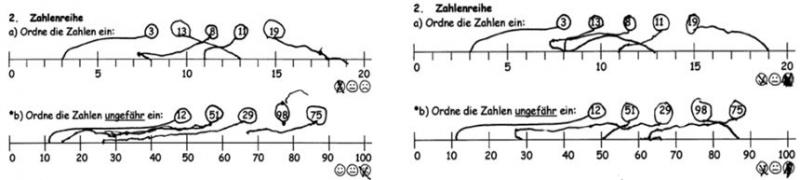
Auch in der Abschluss-Standortbestimmung hat Frieda noch Schwierigkeiten, alle Zahlen richtig zuzuordnen. Woran könnte das liegen?
Einseitig ordinale Zahlvorstellung?
Kinder mit einem einseitig ordinalen Zahlverständnis verstehen Zahlen vornehmlich als Rangplätze. Nach Gaidoschik (2003, S. 28f.) sei es ihnen nicht (oder nur schwerlich) möglich, die Relationen zwischen verschiedenen Zahlen zu erkennen, so z.B. die Relation zwischen Fünf und Acht (Fünf sind drei weniger als Acht, Acht sind drei mehr als Fünf).
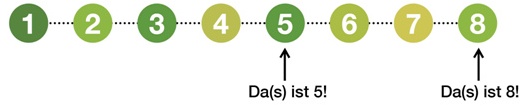
In der Regel beherrschen alle Kinder in der Schule die Zahlwortreihe bis Zehn. Darüber hinaus haben sie gelernt auf die Frage "Wie viele?" zählend zu antworten und tippen dabei i. d. R. jeden einzelnen Gegenstand an; parallel dazu wird die Zahlwortreihe aufgesagt (vgl. Zählprinzipien). Jedoch verbinden nicht alle Kinder mit der Zahlwortreihe auch die Gedanken an eine um eins wachsende Anzahl. Wenn ein Kind beim Zählen bis z. B. Fünf nicht nur diesen einen Gegenstand mit Fünf bezeichnet, sondern alle bisher gezählten (angetippten) Gegenstände mitdenkt. Manche Kinder denken bei Fünf nur an den zuletzt angetippten Gegenstand, als Name für einen bestimmten Platz in einer Reihe (vgl. Gaidoschik 2003).
Nach Gaidoschik (2003) kann dieser fehlerhafte Gedanke ein typisches Anzeichen für eine beginnende Rechenstörung sein.
Wie können diese Kompetenzen aufgebaut werden? Welche Rolle spielt dabei das Material?
Materialien und Anschauungsmittel sollen helfen, mathematische Sachverhalte zu verstehen. Trotzdem sind Anschauungsmittel ebenso Lernhilfe als auch Lerninhalt, zumal sie nicht selbsterklärend sind und Kinder auf sehr unterschiedliche Weise mit ihnen umgehen.
Damit ist gemeint, dass die mathematische Struktur hineingelesen werden muss. Kinder und auch Erwachsene deuten Anschauungsmittel häufig nicht in der intendierten Weise (KIRA o. J.b). Erwachsene haben gelernt, wie Darstellungen zu deuten sind. Oft beruhen diese Deutungen auf Konventionen.
Kinder müssen diese Deutungen erst lernen. Folgendes Beispiel illustriert, wie die - für uns doch eindeutige - Darstellung einer Addition auf dem Zahlenstrahl von Kinder interpretiert werden kann.
Eigenaktivität
Kindern wurde folgende Aufgabe gestellt:
Finde eine passende Aufgabe zu diesem Bild.
 (vgl. KIRA o. J.b)
(vgl. KIRA o. J.b)
Folgendes Gespräch ergibt sich daraufhin zwischen der Lehrerin und Maren:
M: Ich kann das nicht mehr so richtig. Ich konnte das mal ... vor den Ferien.
L: Welche Rechenaufgabe könnte denn zu diesem Bild passen?
M: Mmh, 9 + 13?
L: Warum passt das gut?
M: Weil hier ist ne 9 und hier 13 (zeigt auf die beiden Zahlen)... und von dort (zeigt auf die 9) tut man 13 dazu.
L: Ein anderes Kind meinte, 9 + 4 würde gut passen. Was meinst du dazu?
M: Nee, also die 4 ist ja hier (zeigt auf die 4) und die 9 da (zeigt auf die 9).
Wie kommt Maren zu ihrer Annahme? Es liegt doch auf der Hand, dass der Pfeil von der 9 zur 13 die Rechnung 9 + 4 = 13 veranschaulichen soll. Oder?
"Anschauungsmittel bzw. Arbeitsmaterialien sollen nicht ein Schulleben lang benutzt werden müssen, sondern situationsbedingt und individuell eingesetzt werden und schließlich von sich aus zur (partiellen oder vollständigen) Lösung ermuntern. Damit dies möglich ist, muss das mentale Operieren angeregt und angeleitet werden". (Schmassmann & Moser-Opitz 2008, S.41, Hervorhebung im Original)
Nun stellen sich weiterführende Fragen:
-
Wie kann das mentale Operieren angeregt und angeleitet werden. Im Unterricht wird dieser Aspekt hinsichtlich der passenden Verwendung des Zahlenstrahls konkretisiert.
-
Welches Material ist für welchen Lerninhalt besonders gut geeignet und welche Materialien erscheinen sogar weniger gut geeignet, bestimmte Inhalte in Mathematik zu erlernen? Auf unserer Seite zum Materialeinsatz finden Sie allgemeine Kriterien, die Ihre Entscheidung für das geeignete Material unterstützen können.
Der Zahlenstrahl als ein lineares Anschauungsmittel erfüllt dabei folgende Kriterien für gutes Material:
-
Mit der Zahlenreihe verkörpert er eine fundamentale Idee der Arithmetik (Zahlenreihe).
-
Er ist über die Schuljahre hinweg fortsetzbar und kann für die Orientierung sowie die Rechenoperationen in größeren Zahlräumen sowie anderen Zahlbereichen herangezogen werden.
-
Er ist von den Kindern vergleichsweise problemlos zu zeichnen, handlungsmäßig grundgelegt und im Kopf vorstellbar.
-
Er ermöglicht es den Kindern, eigene dem jeweiligen Wissensstand angepasste Vorgehensweisen zu entwickeln (durch Auswahl der Stützen, der Hilfszahlen, der Zahlen, der Orte, usw.), deren Verschiedenartigkeit den Lernprozess des einzelnen Kindes wie auch der Lerngruppe anregt.
-
Er zeichnet sich durch Übersichtlichkeit und leichte Handhabbarkeit aus und verursacht geringe (bzw. keine) Kosten.
Knackpunkt:
So wichtig der Zahlenstrahl für die Orientierung in neuen Zahlenräumen ist: Beim Rechnen sollte er nicht verwendet werden, da er zum Zählen in Einerschritten verleitet. Für das Rechnen sollte nur auf den leeren Zahlenstrahl - also den Rechenstrich - zurückgegriffen werden.
Obwohl der Zahlenstrahl viele positive Eigenschaften eines guten Materials aufweist, erscheint der Einsatz nicht für jeden Kontext gleichermaßen geeignet. Der Zahlenstrahl enthält vielzählige Konventionen, die erlernt und verstanden werden müssen.
Nachteile:
-
Er lässt sich kaum mit konkreten lebensweltlichen Vorstellungen verbinden.
-
Er ist schwer mit Handlungserfahrungen in Verbindung zu bringen (Wegnehmen und Hinzufügen von Objekten).
-
Der erste Strich ist die Null und nicht die Eins, daraus folgt, dass z. B. die 5 durch den sechsten Strich repräsentiert wird (vgl. Lorenz 1992, S. 151; Steinbring 1994, S. 190).
Anschauungsmittel oder Materialien sollten daher nicht nur in Einführungsphasen, sondern über den gesamten Lernprozess hinweg herangezogen werden. Da Anschauungsmittel nicht automatisch für sich selbst sprechen, sollte den Kindern genügend Zeit und Gelegenheit gegeben werden, um sich mit den jeweils intendierten Bedeutungen und Formen des Gebrauchs vertraut zu machen (vgl. Höhtker & Selter, 1995).
Die Konsequenz für den Unterricht lautet daher, dem gestützten Üben genügend Raum zu geben und den Ablösungsprozess vom Material zu begleiten.
Der leere Zahlenstrahl oder Rechenstrich
Der leere Zahlenstrahl oder Rechenstrich ist eine Linie, an der Zahlen und Rechenoperationen eingetragen werden.
"Der Rechenstrich greift die ordinale Vorstellung von Zahlen auf, wobei ein besonderer Schwerpunkt auf die Beziehungen zwischen den Zahlen gelegt wird. Im Gegensatz zum klassischen Zahlenstrahl, an dem jede Zahl ihre feste Position hat, ist diese Position am Rechenstrich flexibel. Dabei können am Rechenstrich unterschiedliche zentrale Vorstellungen entwickelt und dargestellt werden." (Häsel-Weide, Bartnitzky, Hecker, Lassek & Nührenbörger 2012, S. 18)
Dabei kann er als Arbeitsmittel genutzt werden, an dem die Beziehungen zwischen Zahlen dargestellt werden. Als zentrale Bezugspunkte bei der Orientierung im Hunderterraum dienen Nachbarzehner. Denn diese dienen unter anderem zum überschlagenden Rechnen. Die Zahl in Beziehung zu anderen Zahlen zu sehen, ist für das Rechnen bedeutsam. Z. B. können die Abstände der benachbarten Zehner- und später Hunderterzahlen beim halbschriftlichen Rechnen zum Vereinfachen genutzt werden. Es kann beispielsweise die Hilfsaufgabe berechnet oder schrittweise zum Zehner gerechnet werden (vgl. Häsel-Weide & Nührenbörger 2012).
Eine Unterrichtseinheit, die den Prozess vom konkreten Material zur abstrakten Vorstellung beschreibt, finden Sie im
Unterrichtsteil.