Wie kann das Spiralprinzip im Unterrichtsalltag berücksichtigt werden?
Das Spiralprinzip kann und sollte im Unterrichtsalltag auf der Ebene der Inhalte und der Darstellungsmittel konsequent umgesetzt werden. Aber auch bezogen auf die Auswahl von Aufgabenformaten kann das Spiralprinzip eine wichtige Grundlage bieten.
Am Beispiel des Aufgabenformats „Plusaufgaben mit Reihenfolgezahlen“ (vgl. PIKAS: Modul 2.5) soll im Folgenden gezeigt werden, wie „über mehrere Schulstufen hinweg immer weitere produktive Übungen generiert werden, wobei die Schüler die zugrunde liegenden Strukturen von immer höheren Standpunkten aus überblicken, vertiefen, erweitern und verallgemeinern lernen"(Wittmann 1995, S. 528).Es wird veranschaulicht, wie verschiedene Aufgaben immer wieder über die Jahrgangsstufen hinweg (Wiederholen) mit steigendem Niveau (Vertiefen) im Unterricht eingesetzt werden können, worin sich das Spiralprinzip zeigt und was dabei zu bedenken ist.
Diese Punkte werden genauer betrachtet:
Das Aufgabenformat
Es geht bei dem Aufgabenformat darum, unterschiedlich anspruchsvolle Probleme zu lösen, die sich im Umkreis von Summen aufeinanderfolgender natürlicher Zahlen ergeben. Diese aufeinander folgenden, natürlichen Zahlen (z.B. 1,2,3,..) werden als sogenannte "Reihenfolgezahlen" bezeichnet, die in diesem Aufgabenformat addiert (z.B. 1+2+3+..) werden. Dabei ist die 0 als Summand nicht zugelassen und die Zahlen sind immer der Größe nach geordnet. (vgl. Westermann 2014, S.10)
Die Beispiele in der Tabelle sollen exemplarisch zeigen, welches Summen von Reihenfolgezahlen sind und welche keine Reihenfolgezahlen darstellen:
Summen von Reihenfolgezahlen
2+3+4+5+6
111+112+113
21+22+23+24
68+69
Keine Reihenfolgezahlen
2+3+4+5+4+3
100+200+300
21+23+25+26
90+95
Es lassen sich alle Zahlen – mit Ausnahme der Zweierpotenzen – als Reihenfolgezahlen schreiben. Dabei können ungerade Zahlen immer mindestens als Summe von zwei Reihenfolgezahlen notiert werden. (vgl. Westermann 2014, S.10)
Im Laufe der Schuljahre können die Kinder im Mathematikunterricht kontinuierlich am selben mathematischen Inhalt auf unterschiedlichem Niveau arbeiten, wodurch sich dieses Aufgabenformat gut für einen jahrgangsübergreifenden Unterricht eignet. Dabei ist es grundsätzlich wichtig, dass sich die Kinder regelmäßig über ihre Ergebnisse austauschen, indem sie sich z.B. zu Mathekonferenzen zusammenfinden. Mehr dazu finden Sie auf unserer Partnerseite PIKAS: Infopapier Mathekonferenzen.
Wie das Aufgabenformat in den verschiedenen Schuljahren nun konkret eingesetzt werden könnte wird im nächsten Abschnitt erläutert.
Ziele und Aufgaben in den verschiedenen Klassenstufen
Das Aufgabenformat kann im Kontext der ‚operativen Päckchen’ nach Einführung der Addition im Unterricht eingesetzt werden.
Zur Planung eines spiralig aufgebauten Unterrichts sollten folgende Fragen leitend sein:
-
Welche Ziele werden in den jeweiligen Schuljahren verfolgt?
-
Welche Aufgabenstellungen lassen sich zu den unterschiedlichen Schuljahren entwickeln?
-
Was ist zu bedenken bei der Unterrichtsplanung um den spiraligen Aufbau auch für Kinder erfahrbar zu machen?
Bevor Sie weiterlesen, versuchen Sie doch einmal selbst folgende Aufgabe zu lösen um herauszufinden, vor welcher Herausforderung Kinder stehen.
Eigenaktivität
Wenn man 3 aufeinanderfolgende Zahlen addiert, kann man das Ergebnis immer durch 3 teilen. Warum ist das so?
1./2. Schuljahr
Ziele
-
Anzahlbestimmung von Plättchenmengen
-
Darstellungswechsel fördern
-
Zweiersummen und Verlängern von Reihenfolgezahlen
-
Üben der Addition im Zahlenraum bis 20 unter Nutzung von Beziehungen
-
Beschreiben von Entdeckungen
Aufgabenstellung
-
Wie viele Plättchen sind es? Was fällt dir auf?
-
Schreibe die Plusaufgabe zu den Punktbildern.
-
Wie geht es weiter? Male noch weitere Punktbilder und schreibe die passende Plusaufgabe.
Darum geht es
Zu Beginn sollten Kinder die strukturierte Plättchendarstellung kennen lernen, indem sie die Anzahl von Plättchenmengen bestimmen, benennen und notieren. Inhaltlich geht es um das Üben der Addition im Zahlenraum bis 20 sowie das Erkennen und Ausnutzen von Beziehungen innerhalb aber auch zwischen Aufgaben.
Im Vordergrund steht die Zerlegung von Zahlen in Zweier- und später auch in Dreiersummanden oder mehrere Summanden, wie auch im Schülerdokument beispielhaft zu sehen ist. Die Kinder machen erste grundlegende Entdeckungen, die sie beschreiben können sollten, wie z.B. das Verlängern von Reihenfolgezahlen oder die gleichmäßige Erhöhung zur Ermittlung neuer Zweiersummen: Die erste Zahl wird immer um 1 größer, die zweite Zahl wird ebenfalls immer um 1 größer. Deshalb wird das Ergebnis immer um 2 größer. (Westermann 2014, S.10)
Diese Möglichkeit einer Verlängerung benötigen die Kinder in späteren Sequenzen als "Findungsstrategie" neuer Reihenfolgezahlen. An dieser Stelle könnten Sie nun gemeinsam mit den Kindern ein Strategie-/Entdeckerplakat (siehe Abbildung) erstellen, auf das im späteren Verlauf zurückgegriffen werden kann um die spiralige Entwicklung für die Kinder transparent zu machen.

Mögliche Satzphrasen auf dem Strategie-/Entdeckerplakat:
„Wenn die erste Zahl um 1 größer wird und die zweite Zahl auch, dann wird das Ergebnis um 2 größer.“
„Wenn ich noch eine weitere Zahl dazu plus rechne, erhöht sich das Ergebnis um diese Zahl.“
Ziele
-
Dreiersummen berechnen und Verknüpfung zur Multiplikation
-
Begründung des Zusammenhangs der Dreiersummen und der Multiplikation (in der Abbildung am Beispiel der Mittelzahl mit 3)
-
Geschicktes Zusammenfassen von Summanden
Aufgabenstellung
-
Berechne die Summe von drei Reihenfolgezahlen. Beschreibe oder markiere, was dir auffällt! Kannst du deine Entdeckungen begründen?
-
Finde weitere Zahlen, die du als Summe von drei Reihenfolgezahlen darstellen kannst. Wie findest du schnell heraus, ob sich eine Zahl schreiben lässt? Gibt es einen Trick?
Darum geht es
Nach Einführung der Multiplikation können als
Anknüpfungspunkt zunächst jeweils drei Reihenfolgezahlen addiert werden (z. B.: 2+3+4 oder 7+8+9 oder ...). Anschließend können Aufgabenstellungen gestellt werden die sich ergebende Auffälligkeiten zu erkennen, zu beschreiben und zu begründen.
Dabei wird der Zusammenhang zwischen Dreiersummen und der Multiplikation der Mittelzahl mit 3 (die Strukturierung von Punktbildern dient als Grundlage sowie die Verknüpfung zum Einmaleins) herausgestellt und kann beispielsweise mit Hilfe der Punktedarstellung begründet werden (vgl. Abb.). Die Muster in den strukturierten Punktdarstellungen und das Verschieben der Plättchen stellen bereits erste „Plättchenbeweise“ dar, auf die in der Schullaufbahn immer wieder zurückgegriffen wird. Und auch das geschickte Zusammenfassen der drei Reihenfolgezahlen kann später bei der Zerlegung gerade Anzahlen erneut aufgegriffen werden. Auch erste Überlegungen zum Finden von Aufgaben zu vorgegeben Ergebnisse sind möglich (vgl. Westermann 2014, S. 14).
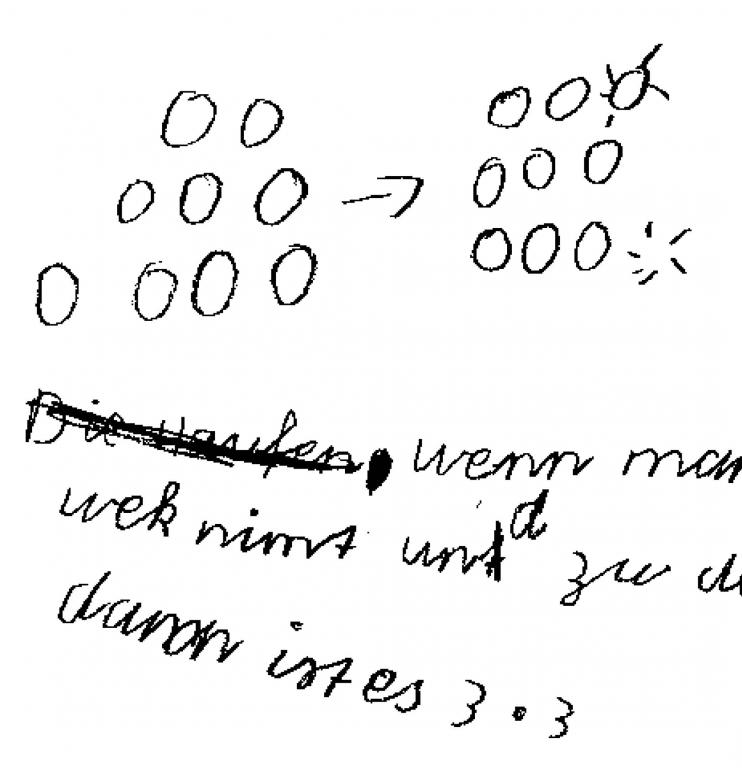
Mögliche Satzphrasen auf dem Strategie-/Entdeckerplakat:
„Wenn die erste Zahl um 1 größer wird und die zweite Zahl auch, dann wird das Ergebnis um 2 größer.“
„Wenn ich noch eine weitere Zahl dazu plus rechne, erhöht sich das Ergebnis um diese Zahl.“
„Das Ergebnis von zwei Zweiersummen erhöht sich um 2.“
„Die Ergebnisse von Zweiersummen sind immer ungerade.“
„Ein Summand ist ungerade und der andere ist gerade, dann ist das Ergebnis ungerade.“
Möglicher Knackpunkt:
Kinder machen nicht von sich aus Entdeckungen bei operativen Päckchen. Dies bedarf Impulsen von Seiten der Lehrperson wie zum Beispiel das Setzen von einem Fokus: „Vergleiche die Ergebnisse, was fällt dir auf?“ oder „Schau dir immer nur die erste Zahl an, erkennst du ein Muster?“. Dabei stehen zunächst reine Beschreibungen der Zusammenhänge im Vordergrund und noch nicht Begründungen. Jedoch sollten diese im perspektivisch angestrebt werden. Es ist aber völlig okay, wenn Kinder nicht alles entdecken und beschreiben und dies auf ihre Art und Weise tun – wie auch in der Abbildung deutlich wird:
 in Anlehnung an: Westermann 2014, S. 10
in Anlehnung an: Westermann 2014, S. 10
Karin entdeckt die Erhöhung der Summanden und kennzeichnet dies mit Pfeilen. Leon erkennt den Zusammenhang zwischen der Summen-Mittelzahl und dem 2. Multiplikator. Sabine vergleicht die Ergebnisse und sieht darin das kleine Einmaleins mit 3.
Wichtig ist es nun, die Entdeckungen der Kinder in den Gesamtzusammenhang einzubetten und die zugrundeliegenden Strukturen gemeinsam zu erarbeiten. Jedes Kind wird auf einer anderen Ebene etwas entdecken und damit schließlich ein Erfolgserlebnis haben können. Weitere Informationen zum Einsatz von Entdeckerpäckchen im Unterricht finden Sie im Selbstlernmodul Üben.
3./4. Schuljahr
Ziele
-
Dreier- und Fünfersummen berechnen und Teilbarkeit erklären
-
Förderung der Argumenationsfähigkeit
Aufgabenstellung
-
Forscherauftrag: Wenn man 3 aufeinanderfolgende Zahlen addiert, kann man das Ergebnis immer durch 3 teilen. Warum ist das so?
-
Addiere immer 5 aufeinander folgende Zahlen. Finde mehrere Aufgaben. Was fällt dir an den Ergebnissen auf? Kannst du das erkären?
-
Untersuche auch Plusaufgaben mit 7 oder 9 aufeinander folgenden Zahlen.
Darum geht es
In dieser Unterrichtssequenz geht es darum, dass die Kinder das Aufgabenformat der „Plusaufgaben mit Reihenfolgezahlen“ vertiefend kennen lernen. Als Einstieg bietet sich zur Anknüpfung an das Vorwissen an, dass die Kinder zunächst aus 5 Beispielen richtige und falsche Aufgaben mit Reihenfolgezahlen identifizieren und ihr Verständnis der Aufgabenstellung durch Notation einiger „Plusaufgaben mit Reihenfolgezahlen“ auf einem Blatt auffrischen.
Anschließend geht es darum, Dreier-und Fünfersummen geschickt zu berechnen, Entdeckungen festzuhalten und die Teilbarkeit zu erklären. Auch ein Transfer auf Siebener und Neunersummen ist denkbar sowie die Gauss-Aufgabe (Wie konnte Carl Gauß ganz schnell die Summe aller Zahlen von 1 bis 100 herausfinden?) bereits an dieser Stelle zu thematisieren.

Ausblickend auf die „nächste Entwicklungszone“ könnte hier bereits die Zahl 15 in unterschiedlichen Summen herausgearbeitet werden.
Bild vom Strategie/Entdeckerplakat:
„Wenn die erste Zahl um 1 größer wird und die zweite Zahl auch, dann wird das Ergebnis um 2 größer.“
„Wenn ich noch eine weitere Zahl dazu plus rechne, erhöht sich das Ergebnis um diese Zahl.“
„Das Ergebnis von zwei Zweiersummen erhöht sich um 2.“
„Die Ergebnisse von Zweiersummen sind immer ungerade.“
„Ein Summand ist ungerade und der andere ist gerade, dann ist das Ergebnis ungerade.“
„Die Summen wachsen um die Anzahl an Summanden.“
Verlängerungsstrategie: Hinten verlängern z.B. 2+3 à 2+3+4 à 2+3+4+5
Möglicher Knackpunkt:
Schwierigkeiten bestehen häufig im Verstehen, bei der Produktion der Lösung und dem anschließenden Begründen der Vorgehensweise.
Deswegen sollten die Kinder zunächst sämtliche Summen niederschreiben, die sie finden. Dadurch wird auch gleichzeitig an das Vorwissen angeknüpft. Am Ende dieser Phase sollten die Kinder in „Rechenkonferenzen“ an Gruppentischen mit zur gleichen Zeit fertig werdenden anderen Zweiergruppen ihre Ergebnisse abgleichen bzw. ergänzen und dabei möglicherweise schon erste Diskussionen über Findungsstrategien führen, wie alle Zahlen gleichmäßig erhöhen oder vermindern, beim Nachfolger - der letzten Zahl oder dem Ergebnis beginnen.
4.-6. Schuljahr
Ziele
-
Vierersummen
-
Finden aller Summen mit Reihenfolgezahlen, deren Ergebnis nicht größer als 25 ist
-
Verallgemeinerungen
-
Förderung der Problemlöse- und Argumentationsfähigkeit
Aufgabenstellung
-
Finde möglichst viele Plusaufgaben mit Reihenfolgezahlen. Das Ergebnis soll nicht größer als 25 sein. Wie bist du vorgegangen? Was ist dir aufgefallen? Wie kannst du überprüfen, ob du alle gefunden hast?
-
Berechne die Summe von vier Reihenfolgezahlen. Beschreibe oder markiere, was dir auffällt. Wie kannst du schnell Vierersummen ausrechnen?
-
Finde weitere Zahlen, die sich als Summe von vier Reihenfolgezahlen darstellen lassen. Wie findest du schnell heraus, ob sich eine Zahl schreiben lässt? Gibt es einen Trick?
Darum geht es
Als Anker könnten die Kinder zunächst einige Reihenfolgezahlen aufschreiben und dann dazu aufgefordert werden, nur die zu behalten, bei denen das Ergebnis nicht größer als 25 ist. Die Aufgabenstellung ab Ende des 4. Schuljahrs und der weiterführenden Schuljahre besteht darin, alle Summen aufeinanderfolgender natürlicher Zahlen zu finden, deren Resultat nicht größer ist als 25. Sie können es gerne einmal selbst ausprobieren. Insgesamt gibt es 27 verschiedene Lösungen. Dabei können erste Verallgemeinerungen formuliert werden: Welche Zahlen lassen sich als Fünfer- oder Siebenersummen schreiben? Es ergeben sich viele Fragestellungen und immer mehr rückt die Schulung der Argumentationsfähigkeit in den Fokus.
Außerdem können an dieser Stelle die Vierersummen ausgehend von den Zweiersummen genauer erörtert auf "geschickte" Berechnungen sowie ein Transfer auf Sechsersummen und auch hier erste Verallgemeinerungen formuliert werden. Falls noch nicht zuvor thematisiert, kann dabei ebenfalls die Gauß-Aufgabe angesprochen werden.
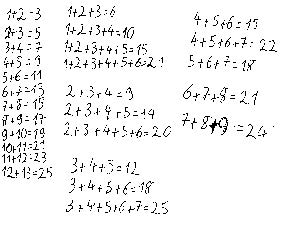
Bild vom Strategie/Entdeckerplakat:
„Wenn die erste Zahl um 1 größer wird und die zweite Zahl auch, dann wird das Ergebnis um 2 größer.“
„Wenn ich noch eine weitere Zahl dazu plus rechne, erhöht sich das Ergebnis um diese Zahl.“
„Das Ergebnis von zwei Zweiersummen erhöht sich um 2.“
„Die Ergebnisse von Zweiersummen sind immer ungerade.“
„Ein Summand ist ungerade und der andere ist gerade, dann ist das Ergebnis ungerade.“
„Die Summen wachsen um die Anzahl an Summanden.“
Verlängerungsstrategie: Hinten verlängern z.B. 2+3 à 2+3+4 à 2+3+4+5
Vorne verlängern z.B. 4+5+6 à 3+4+5+6 à 2+3+4+5+6
Verkürzen z.B. 3+4+5+6 à 4+5+6 oder 3+4+5
Alle Summanden um 1 erhöhen: 2+3+4 à 3+4+5
Bei der nächsten Zahl beginnen: 2+3+4 à 3+4+5 à 4+5+6
Möglicher Knackpunkt
Das Finden und anschließende Erklären wird den Kindern nicht leicht fallen. Zu Beginn werden die Kinder vermutlich zunächst einmal ausprobieren bzw. diejenigen Möglichkeiten nennen, die ihnen spontan einfallen. Nach einer gewissen Anlaufzeit lassen sich dann systematischere Findestrategien beobachten, die die Kinder bereits bei anderen Aktivitäten zu diesem Aufgabenformat aufgestellt haben könnten, so dass an dieser Stelle ein Anker in Form eines "Stratgieplakats" denkbar wäre, welches nun an dieser Stelle wieder genutzt werden sollte. Die Kinder können so besser an ihr Vorwissen anknüpfen. Zu diesen Findestrategien zählen u.a. das Hinten oder Vorne Verlängern, Hinten oder Vorne verkürzen, alle erhöhen oder vermindern, Nachfolger – letzter Zahl oder beim Ergebnis beginnen. Das Hinten verlängern könnten die Kinder bereits in der Schuleingangsphase kennengelernt haben oder aber bereits in einer anderen Aktivität zum Aufgabenformat, so dass auch dieses Vorwissen verknüpft werden kann und sollte.
Nach der Einzelphase ist es wichtig, dass sich die Kinder in Rechenkonferenzen zusammenfinden und sich über ihre gefundenen Reihenfolgezahlen austauschen.
Am Ende dieser Sequenz sollten die Gruppen anhand ihres gemeinsam erstellten Dokuments die anderen Kinder von der Richtigkeit ihrer Überlegungen überzeugen. Hierzu ist es am sinnvollsten das erstellte Gruppendokument rasch auf eine Tageslichtschreiberfolie zu kopieren. Dann können die Kinder argumentierten, warum sie der Auffassung seien, dass die Anzahl ihrer gefundenen Lösungen die richtige sei.
Für eine Rückschau des Gelernten ist es sinnvoll, die Kinder individuell nach ihrem Lernprozess zu befragen mit Fragen wie beispielsweise: „Was hast du über Reihenfolgezahlen gelernt?“ – denn schriftliche Rückmeldungen sind sehr anspruchsvoll!
Wie im Eingangsbeispiel der Satz des Mädchens deutlich gemacht hat „Genau, das kennen wir ja aus dem letzten Schuljahr“ sollten natürlich bei jeder erneuten Begegnung mit dem Thema die Aufgabenstellungen wieder aufgegriffen werden, die die notwendige Basis zur Bearbeitung weiterer Aufgaben darstellen und an die Lernvoraussetzungen der Kinder angepasst sind. Denn Kinder sollen an ihre vorhandenen Vorstellungen und Kompetenzen anknüpfen können. Doch damit dies gelingen kann, müssen die inhaltlichen Themenstränge, anhand derer sich der Unterricht spiralförmig entwickelt, sichtbar gemacht und an zentralen Stellen sogenannte "Anker" gesetzt werden. (vgl. Büchter 2014, S.7) Eine Möglichkeit solch einen Anker zu setzen besteht in der Verwendung von Wortspeichern und Strategieplakaten – wie am Beispiel aufgezeigt, die kontinuierlich gemeinsam mit den Kindern zu den verschiedenen Themenbereichen weiterentwickelt und passend zum Thema wieder eingebracht werden können.
Ausführliche Hinweise zur Unterrichtsdurchführung und ausgearbeitete Materialien für die Kinder befinden sich im Materialteil und auf unserer Partnerprojektseite PIKAS: Langfristige Lernprozesse .
Es lohnt sich die Zeit in die Vorbereitung des Unterrichts zu investieren und Kindern die Möglichkeit zu geben, fachlichen Gegenständen frühzeitig zu begegnen, sie wieder aufzugreifen und zu vertiefen.
Weitere Anregungen für den Unterricht und auch andere Themen finden Sie im Materialteil.