Unterrichtsideen zur Ablösung vom zählenden Rechnen
Im Hintergrund konnten Sie lesen, dass die Voraussetzungen für das (flexible) Rechnen sehr vielfältig sind. Diese Vielfalt an notwendigem mentalen Werkzeug macht deutlich, dass die Ablösung vom zählenden Rechnen weder mit einer „Unterrichtseinheit“ gelingen, noch mit einigen wenigen Übungsformaten vorbereitet werden kann. Vielmehr müssen diese Werkzeuge im Unterricht immer wieder gemeinsam in den Blick genommen werden und sich langsam zu einem mentalen „Werkzeugkoffer“ etablieren. Dafür finden sie auf dieser Seite folgende Aspekte:
-
Nicht-zählendes Vorgehen unterstützen
-
Das Format Schnelles Sehen
... gemeinsam mit allen Kindern
... in Partner- oder Kleingruppenarbeit
... in Einzelarbeit
-
Viele weitere Unterrichtsideen zur Ablösung vom zählenden Rechnen
Nicht-zählendes Vorgehen unterstützen
Im Einstiegsbeispiel konnten Sie sich mit Stefanies Vorgehen beim Lösen der Aufgabe 6+8 beschäftigt. Zur Erinnerung: Sie ist zählend vorgegangen und auf diese Weise zu einem richtigen Ergebnis gekommen.
Wie viel „wert“ ist das richtige Ergebnis, wenn Stefanie Erstklässlerin ist? Wie viel ist es „wert“, wenn sie Viertklässlerin ist? Wie viel, wenn Sie in der achten Klasse ist? Diese Überlegungen machen vielleicht deutlich, dass richtige Ergebnisse im Mathematikunterricht möglicherweise wünschenswert sind und sicherlich manchmal auch Indikator für erfolgreiches Lernen sein können, aber mit Sicherheit nicht das einzige, worauf Lehrkräfte, Schüler und Schülerinnen sich konzentrieren sollten.
Im Beispiel wird nämlich auch deutlich, dass Stefanie bereits viele sehr gute und tragfähige Lösungsschritte nutzt und bereits über viele Kompetenzen verfügt: Stefanie weiß, dass sie die Tauschaufgabe nutzen darf und nutzt sie auch, weil sie schon weiß, dass diese Strategie ihr Arbeit abnimmt; sie weiß, dass acht größer ist als sechs; sie kann Sechs mit den Fingern zeigen, ohne zu zählen; ...
All diese Kompetenzen sind für ein erfolgreiches Weiterlernen sehr viel wichtiger, als das richtige Ergebnis 14. Daher sollten diese Kompetenzen mit Stefanie weiter gefestigt werden und können Ausgangspunkt sein für erfolgreiches Weiterlernen.
Am Beispiel der Unterrichtsidee „Schnelles Sehen“ wird im Folgenden gezeigt, wie gemeinsam nicht-zählende Prozesse in den Blick genommen werden können, und dass richtige Ergebnisse sogar nebensächlich werden können.
Das Format ,,Schnelles Sehen''
Die Frage Wie viele sind das? wird Kindern bereits vor Schuleintritt häufig gestellt (und nicht selten stellen sie sie selbst), doch spätestens in der ersten Klasse und mit der Erarbeitung der Zahlen, ihrer Beziehungen und des Zahlenraums ist diese Frage ein fester Bestandteil des Mathematikunterrichts.
Sie kann auch mit dem Ziel gestellt werden, die Ablösung vom zählenden Rechnen zu unterstützen und Kinder anzuregen Zahlbeziehungen und -zusammenhänge zu sehen und zu nutzen. Dabei sollte jedoch der Fokus vor allem auf der nicht-zählenden Anzahlermittlung liegen.
Das Format Schnelles Sehen ist dabei eine gute Möglichkeit, die gemeinsame Aufmerksamkeit auf die Zahlbeziehungen und das Nutzen von Strukturen zu richten. Die viel wichtigere Frage lautet in diesem Kontext jedoch: Woher weißt du das?
Das Schnelle Sehen (oder auch quasi-simultane Zahlauffassung, oder Blitz-Blick-Übungen)
bietet nicht nur für den Anfangsunterricht erstaunlich viele Lernmöglichkeiten für Schülerinnen und Schüler. Diese Lernmöglichkeiten sind sowohl prozess- als auch inhaltsbezogen und zwar auf sehr verschiedenen Leistungsniveaus. Zu den wichtigsten inhaltsbezogenen Lernzielen gehören
-
die Entwicklung und Nutzung eines Teil-Ganzes-Verständnisses,
-
das Erkennen, Deuten und Nutzen von arithmetischen Strukturen und
-
das Sehen und Nutzen von Zusammenhänge zwischen Zahlen und Operationen
Das Schnelle Sehen zielt unter anderem auf die gedankliche Rekonstruktion von etwas Gesehenem, weil auf diese Weise mentale Vorstellungsbilder entstehen können.
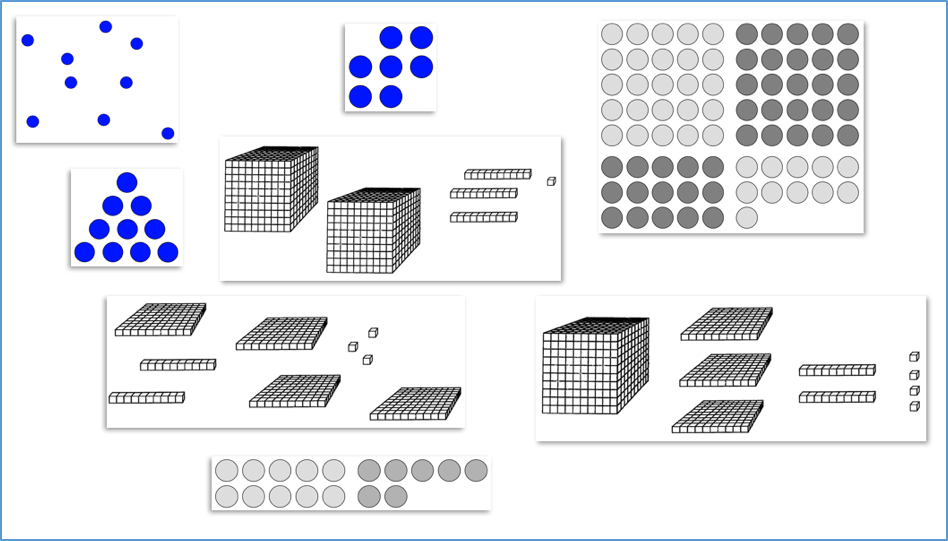 Abbildung 1: Verschiedene Mengendarstellung in verschiedenen Zahlenräumen zum „schnell Sehen“
Abbildung 1: Verschiedene Mengendarstellung in verschiedenen Zahlenräumen zum „schnell Sehen“
Beim Schnellen Sehen wird den Kindern eine Menge gezeigt – jedoch nur kurz. Aufgabe der Kinder ist es dann zu erklären, wie sie die entsprechende Menge gesehen haben – die korrekte Anzahl ist dabei nachrangig.
Schnelles Sehen mit allen Kindern - Das Format vorstellen
Bereits früh im ersten Schuljahr kann das Schnelle Sehen (vor allem mit kleinen Mengen) mit den Schülerinnen und Schülern als wiederkehrendes Format genutzt werden.
Es hat sich gezeigt, dass eine Durchführung des Formats mit vielen Kindern gemeinsam nicht nur unterrichtspraktisch von Vorteil ist (weil man es dann nicht immer neu erklären muss), sondern auch von der Sache her: Je mehr Kinder beim Schnellen Sehen mitmachen, desto reichhaltiger sind die Beiträge zu den Impulsfragen und Anregungen: Was genau hast du gesehen? Beschreib mal. Woher weißt du, wie viele es sind?
Mögliche Impulsfragen und -anregungen beim Schnellen Sehen
-
Woher weißt du, wie viele es sind?
-
Wer hat das noch anders gesehen?
-
Beschreibe noch einmal, wie Peter das gesehen hat.
-
Du kannst es nicht genau sagen? Gibt es Ausschnitte bei denen du dir sicher bist? Wie sahen die aus?
-
Wie viele Punkte waren es höchstens? Wie viele mindestens?
-
Waren das mehr (oder weniger) als 5, 10, 20, 50, 100, 500, 1000, ...?
-
Schreib mal eine passende Aufgabe (passende Zahlen) dazu auf, was du gesehen hast.
-
Zeig nochmal am Material, was du gesehen hast.
Für die Vorstellung des Formats mit vielen Kindern empfiehlt sich die Verwendung eines Overhead-Projektors oder eines Whiteboards, weil hier für alle Kinder sichtbar auf einer großen Fläche die Mengen für kurze Zeit gezeigt werden können. Beim OHP können die Mengen mit Plättchen oder vorbereiteten Folien (siehe Material) kurz gezeigt werden (durch Abdecken oder An- und Ausschalten); beim Whiteboard durch eine entsprechende Präsentation.
Die Aufgabe der Lehrkraft ist es nun, durch geschickte Impulsfragen (siehe oben) die Aufmerksamkeit der Schülerinnen und Schüler auf die Zahlbeziehungen und Strukturen der gesehenen Menge zu richten.
Worauf kann ich als Lehrkraft achten?
-
Wert legen auf das Beschreiben des Gesehenen:
Gute, das heißt nachvollziehbare Beschreibungen und Begründungen werden verstärkt (und nicht ausschließlich das Nennen der richtigen Anzahl). Dadurch erleben die Schülerinnen und Schüler die Kommunikation über mathematische Sachverhalte als festen Bestandteil des Mathematiklernens.
So kann so eine konstruktive Fehler- und Gesprächskultur etabliert werden: Ergebnisse sind nachrangig, wenn die Begründung nachvollziehbar ist („Sehr gut, du hast also acht gesehen, weil du drei und fünf gesehen hast.“). Hinzu kommt, dass gut nachvollziehbaren Beschreibungen im Nachhinein nicht geschmälert werden, wenn die beschriebene Menge nicht mit dem Gezeigten übereinstimmt.
-
Die korrekte Anzahl wird am Ende der Diskussion nicht gezeigt oder genannt...:
... auf jeden Fall nicht immer. Viele Unterrichtsversuche haben gezeigt, dass es Schülerinnen und Schülern nichts ausmacht, wenn das Schnelle Sehen nicht „aufgelöst“ wird – aber nur dann nicht, wenn im Vorfeld gute Erklärungen gefordert, thematisiert und somit verstärkt wurden.
-
Verknüpfen verschiedener Darstellungsebenen:
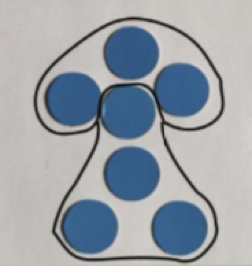
Um tragfähige Grundvorstellungen zu Zahlen und ihren Beziehungen zu entwickeln, ist es wichtig, verschiedene Darstellungsebenen immer wieder zu verknüpfen. Dies kann auf verschiedenen Wegen Geschehen. Zum Beispiel kann das Gesehene während der Beschreibung nachgezeichnet oder nachgelegt werden, und ebenso kann es parallel auch symbolisch dokumentiert werden.
 Bildrecht C. Schülke
Bildrecht C. Schülke
 Bildrecht A. Schulz
Bildrecht A. Schulz
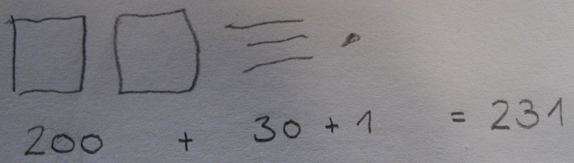 Bildrecht A. Schulz
Bildrecht A. Schulz
-
Verknüpfen verschiedener Schülerantworten und Heterogenität nutzen:Wenn das Schnelle Sehen mit mehreren Kindern durchgeführt wird, dann werden automatisch verschiedene gesehene Anzahlen genannt („Ich habe acht gesehen, da waren viermal jeweils zwei“ – „Nein, das waren sieben, weil da waren drei und drei und noch einer, ganz am Rand.“). Aufgabe der Lehrkraft ist es nun, diese verschiedenen Aussagen zu vernetzen und zu bündeln.
Schnelles Sehen zu zweit oder in kleinen Gruppen
Wenn alle Schülerinnen und Schüler das Format Schnelles Sehen kennen und auch vertraut sind mit möglichen Kommunikationsmustern bei diesem Format (siehe Impulsfragen), dann kann das Schnelle Sehen auch in Partnerarbeit oder in Kleingruppen gelingen.
Als Partner- oder Gruppenformat bekommt das Schnelle Sehen einige zusätzliche spannende Aspekte:
-
Es kann sinnvoll sein, dass die Schülerinnen und Schüler sich vorher auf einen Zahlenraum einigen, oder auf eine bestimmte Art der Anordnung („Aber nicht alles einfach nur in eine Reihe.“), oder auf ein bestimmtes Arbeitsmittel („Zuerst am Rechenrahmen und nachher wieder mit dem Dienes-Material.“)
-
Fast automatisch versuchen die Kinder nun, besonders „leichte“ oder „schwere“ Anordnungen zu legen.
-
Diese erklärte Absicht kann im Folgenden dazu führen, dass sich die Kinder darüber austauschen, ob und warum bestimmte Anordnungen leicht und schnell zu sehen waren (oder nicht).
-
Im Anschluss daran können ggf. Umstrukturierungen vorgenommen werden, um die Anordnung (subjektiv) noch besser erkennbar zu machen.
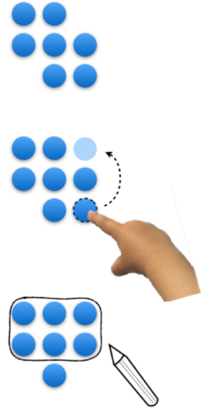
Und alleine...? – Schnelles Sehen in Einzelarbeit
Eigenaktivität
Welches der folgenden Bilder ist wohl besonders „leicht“ oder „schwer“ zu deuten und zu beschreiben, wenn man es nur kurz sieht? Warum?

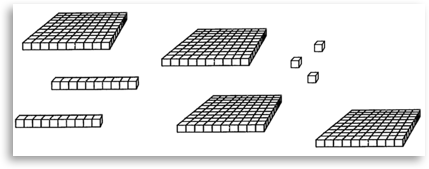 Bildunterschrift
Bildunterschrift


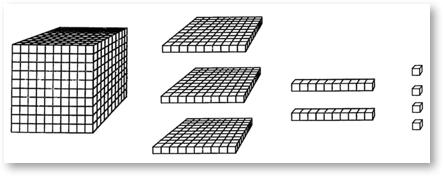

Sortieren und Markieren
Genau das, was Sie gerade in der Eigenaktivität gemacht haben, können Schülerinnen und Schüler im Mathematikunterricht machen: Vorgegebenen Anordnungen sortieren nach den Merkmalen „Das kann ich schnell sehen“ und „Das kann ich nicht schnell sehen“.


Wie in Abbildung 2.1 und 2.2 zu sehen ist, gibt es dabei keine „richtige“ oder „falsche“ Sortierung, sondern diese können individuell sehr verschieden sein. Wichtig ist dann, dass die Schülerinnen und Schüler begründen, warum sie die einzelnen Bilder in dieser Weise einsortiert haben. Eine gute Möglichkeit bietet hier das Markieren der Vorlagen, bei dem die Kinder „ihre“ Strukturierungen einzeichnen können.
Natürlich ist auch der Austausch über verschiedene Zuordnungen durch verschiedene Kinder zum Beispiel im Rahmen eines Museumsgangs möglich. Dabei können die Kinder an (für sie) spannenden, fraglichen, gut nachvollziehbaren, ... Sortierungen stehen bleiben und sich austauschen.
Weitere Unterrichtsideen für die Ablösung vom Zählenden Rechnen
Viele weitere Unterrichtsideen, die ihren Teil zur Ablösung vom zählenden Rechnen beitragen, finden Sie zum Beispiel auf der Primakom-Seite und auf der Seite „Mathe inklusiv mit PIKAS“:
Diese Seite wurde erstellt von Axel Schulz für das primakom-Team.