Gestaltung und Einsatz informativer Aufgaben zur Leistungsfeststellung
Die Grundschule ist „einem pädagogischen Leistungsverständnis verpflichtet, das Leistungsanforderungen mit individueller Förderung verbindet“ (MSW NRW 2008, S. 16). Mathematikbezogene Leistungen von Schülerinnen und Schüler wahrzunehmen, stellt eine bedeutsame und anspruchsvolle Aufgabe für Lehrende dar.
Im Folgenden wird dazu auf nachfolgende Fragen eingegangen:
Welche Anforderungen sind an Leistungsfeststellungen im Mathematikunterricht zu stellen?
Eine wesentliche Aufgabe der Schule besteht in einer Leistungsfeststellung, die Leistungen einzelner Schülerinnen und Schüler nicht nur abzuprüfen, sondern insbesondere, um Lernentwicklungen und -ergebnisse der Kinder zu dokumentieren, um die Grundlagen für eine individuelle Förderung zu schaffen. Neben den Erläuterungen auf dieser Seite finden Sie Hinweise dazu ebenfalls unter Standortbestimmungen.
Einwicklungsfunktion statt Auslesefunktion
Die Entwicklungsfunktion von Leistungsfeststellung zielt auf die bestmögliche Bildungsentwicklung der Kinder und beinhaltet
-
die Berücksichtigung individueller Entwicklungsmöglichkeiten
-
das Anstreben erreichbarer Ziele für das einzelne Kind
-
Ermutigung zur Anstrengung
-
Stärkung des eigenständigen Lernens
-
Förderung persönlicher, sachbezogener und sozialer Kompetenzen
-
Würdigung individueller Fortschritte.
Die Auslesefunktion dagegen zielt auf die innerschulische und nachschulische Auslese der Kinder und trifft Entscheidungen über:
-
Versetzungen und Nichtversetzungen
-
Schullaufbahnen
-
Abschlussniveaus.
Die Auslesefunktion hat folglich ihre Berechtigung. Sie wird in der Wahrnehmung der Eltern und der Kinder immer dann deutlich, wenn Noten vergeben und Leistungsspiegel veröffentlicht werden.
„Schule kann dieses Spannungsverhältnis von Entwicklungsfunktion und Auslesefunktion schlichtweg nicht beseitigen. Aber sie kann trotz dieses Dilemmas versuchen, mit den Leistungen der Kinder verantwortlich umzugehen, also durch individuelle Förderung die Lernfreude der Kinder zu erhalten und deren Leistungsfähigkeit zu entwickeln. Das ist das Konzept der pädagogischen Leistungsschule" (Selter 2006, S. 8).
Leistungen sollten fachbezogen festgestellt werden, daher wird im folgenden Abschnitt aufgezeigt, welche Voraussetzungen und Bedingungen Leistungsfeststellungen in der Schule, speziell im Mathematikunterricht erfüllen sollten. Die folgende Tabelle liefert eine Beschreibung von sieben Leitideen zur Leistungsfeststellung (nach Selter, 2006).
kompetenzorientiert
Äußerungen und Handlungen von Kindern sind oft vernünftiger und organisierter, als es aus der Erwachsenensicht scheint. Lehrerinnen und Lehrer sollten ihre Wahrnehmung auf die Kompetenzen der einzelnen Kinder und dessen Denkwege richten, und weniger auf Fehler oder Defizite.
kontinuierlich
Leistungsfeststellung sollte nicht auf einen besonderen Zeitpunkt bzw. ein Ereignis beschränkt sein (z.B. Klassenarbeit). In allen Phasen des Unterrichts sollten Leistungsbewertung und Reflexion über Leistungen ihren Platz finden.
prozessorientiert
Leistungsfeststellung sollte sich nicht einseitig auf die Produkte des Lernens richten, sondern sich ebenso den Lernprozess berücksichtigen.
transparent
Schülerinnen und Schüler sollen ihre eigene Arbeit sowie ihre Lernerfolge reflektieren und selbst steuern können. Daher sollte den Kindern ein altersangemessenes Maß an Transparenz ermöglicht werden, da sich dies förderlich auf das Gelingen von Lernprozessen und die Qualität auswirkt.
informativ
Damit die Leistungsfeststellung Ausgangspunkt für die individuelle Förderung der Schülerinnen und Schüler sein kann, muss sie auch informativ sein. Hierfür ist neben den alternativen und kontinuierlichen Formen der Leistungsfeststellung auch die Wahl der Aufgaben ausschlaggebend.
differenziert
differenziertLeistungsfeststellungen sollen aufgrund individueller Unterschiede differenziert und ggf. mit unterschiedlichen Leistungsanforderungen erfolgen. Beispielsweise kann das Aufgabenangebot nach Grundanforderungen und weiterführenden Anforderungen differenziert werden.
umfassend
Klassenarbeiten und Tests allein sind weniger geeignet, ein authentisches Bild dessen, was Kinder leisten können zu erhalten. Daher sollte ein breites Spektrum an Instrumenten zum Einsatz kommen:
-
beiläufige und systematische Beobachtungen
-
Standortbestimmungen
-
Arbeitsprodukte, Sammelmappen, Präsentationen, Forscherhefte
-
usw.
Eine wesentliche Aufgabe der Grundschule ist es, „Kinder an schulische Leistungsanforderungen und den produktiven Umgang mit der eigenen Leistungsfähigkeit heranzuführen ... Für den Unterricht bedeutet dies, Leistungen nicht nur zu fordern, sondern sie auch zu ermöglichen, wahrzunehmen und zu fördern“ (MSW NRW 2008, S. 16). Wie im Einstiegsbeispiel angedeutet, steht Leistungsfeststellung und -bewertung in der Schule häufig im Zusammenhang mit Klassenarbeiten, in denen vornehmlich inhaltsbezogene Kompetenzen abgeprüft werden.
Zeitgemäßer Mathematikunterricht berücksichtigt neben den inhaltsbezogenen Kompetenzen ebenso die prozessbezogenen Kompetenzen. Auf vielen unserer Seiten haben wie kennengelernt, wie Sie die Förderung diese in den Unterricht sinnvoll integrieren können. Wenn die prozessbezogenen Kompetenzen einen großen Teil des Mathematikunterrichts ausmachen, dann sollten sie ebenso in die Leistungsfeststellung und -bewertung einfließen. Dies kann beispielsweise durch sogenannte informative Aufgaben geschehen.
Wodurch zeichnen sich informative Aufgaben aus?
Um die Lernstände der Kinder wahrnehmen zu können, bedarf es diagnostischer Methoden. Beim Einsatz dieser Methoden ist eine sorgfältige Aufgabenauswahl wichtig, denn erst durch geeignete Aufgaben können Informationen über die Kompetenzen und Lösungswege der Kinder gewonnen werden. Doch welche Art von Aufgaben eignet sich für die Erhebung von Denkwegen?
Rein produktorientierte Aufgaben, bei denen es nur um richtig oder falsch geht, ermöglichen dem Lehrer nur selten Einblicke in Denkwege der Kinder. Es ist kaum möglich, bei falschen oder fehlerhaften Lösungen festzustellen, ob diese etwa auf mangelnder Konzentration, Rechenfehlern oder auf Fehlvorstellungen beruhen.
Gut eignen sich hingegen sogenannte informative Aufgaben, bei denen man, wie es der Name schon sagt, mehr und detailliertere Informationen über Denkwege der Kinder erhält (vgl. KIRA: Informative Aufgaben).
Ein Beispiel:
Kinder in der 2. Klasse wurden vor die Aufgabe gestellt, möglichst genau eine analoge Uhr zu zeichnen.
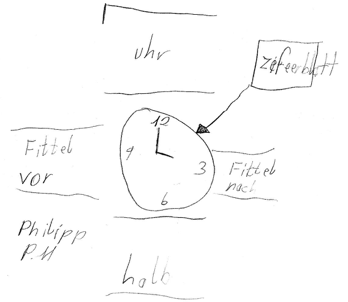
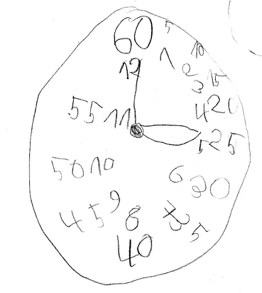
Die beiden Uhrenbilder unterscheiden sich deutlich voneinander:
Beide Zeichnungen lassen sich eindeutig als Uhr identifizieren, jedoch können unterschiedliche Informationen über die Vorerfahrungen der Kinder aus den Zeichnungen entnommen werden.
Anhand folgender oder ähnlicher Fragen lassen sich Vorerfahrungen der Kinder strukturieren:
-
Welche Vorstellungen haben sie über den Aufbau einer Uhr entwickelt? Wie sehen die Kinder die Uhr?
-
Was ist ihnen besonders wichtig?
-
Wie differenziert kennen die Kinder Merkmale normierter Messgeräte? Welche Teile der Uhr nehmen sie in die Zeichnung auf?
Werfen wir nun einen Blick auf die beiden Schülerdokumente:
Philipp trägt in seine Uhr (Abb. 1) die Zahlen 3, 6, 9 und 12 und zwei unterscheidbare Zeiger ein.
Zusätzlich beschriftet er seine Zeichnung und benennt verschiedene Teile (Uhr, Ziffernblatt).
Außerdem gibt er Hinweise zum Ablesen der Uhrzeit (viertel nach, halb, viertel vor).
Aus Noras Zeichnung (Abb. 2)
erhalten wir andere Informationen. Sie zeichnet ebenfalls zwei unterscheidbare Zeiger, trägt jedoch alle Zahlen von 1 bis 12 auf ihr Ziffernblatt ein. Zusätzlich beschriftet sie das Ziffernblatt mit Minutenangaben von 5 bis 60 in Fünferschritten, die jeweils neben den Zahlen 1 bis 12 stehen.
Merkmale informativer Aufgaben
Es stellt sich die Frage, durch welche Kriterien sich eine informative von einer sogenannten geschlossenen Aufgabe unterscheidet? Der Unterschied zwischen geschlossenen und informativen Aufgaben wird hier an einem Beispiel verdeutlicht.
Grundsätzlich sind informative Aufgaben offen gestaltet, d.h. den Schülerinnen und Schülern wird viel Freiraum zur Bearbeitung gegeben. Lösungswege sind nicht vorgeschrieben, sondern im Gegenteil sollten mehrere plausible Lösungen möglich sein. Durch die Möglichkeit die Aufgabe dem individuellen Vermögen zu bearbeiten, erhält man aufschlussreiche Informationen über das Denken der Kinder und deswegen sind sie informativ.
Eigenaktivität
Schauen Sie sich dazu bitte die beiden folgenden Abbildungen unter der genannten Fragestellung an. Welche Informationen erhalten sie über den Lernstand des Kindes?
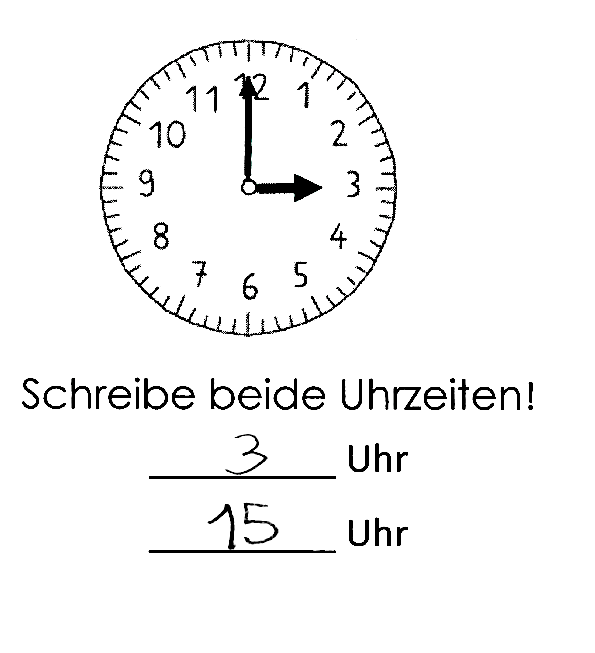 Aufgabenstellung: Schreibe beide Uhrzeiten
Aufgabenstellung: Schreibe beide Uhrzeiten
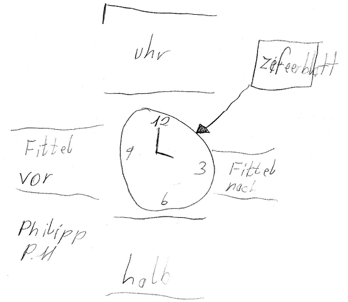 Aufgabenstellung: Zeichne eine Uhr, auf der es drei Uhr ist.
Aufgabenstellung: Zeichne eine Uhr, auf der es drei Uhr ist.
Offene Aufgabenstellungen, bei denen die Kinder nicht nur Ergebnisse aufschreiben, sondern auch erklären sollen, wie bzw. warum sie so gerechnet haben, haben einen Mehrwert. Denn erst durch die Begründung des Kindes (vgl. Eigenaktivität) wird deutlich, dass es die Aufgaben nicht losgelöst voneinander ausrechnet, sondern die Zusammenhänge zwischen den Aufgaben entdeckt und ausnutzt - was nicht selbstverständlich ist. Diese wichtige Information hätte man jedoch ohne die Erklärung des Kindes nicht erfahren.
Ein zweites Beispiel verdeutlicht den Mehrwert einer offen gestellten Aufgabe im Hinblick auf die Kompetenz Uhrzeiten kennen.
Im folgenden Beispiel sehen sie zwei unterschiedliche Aufgabenbearbeitungen von Jasemin.
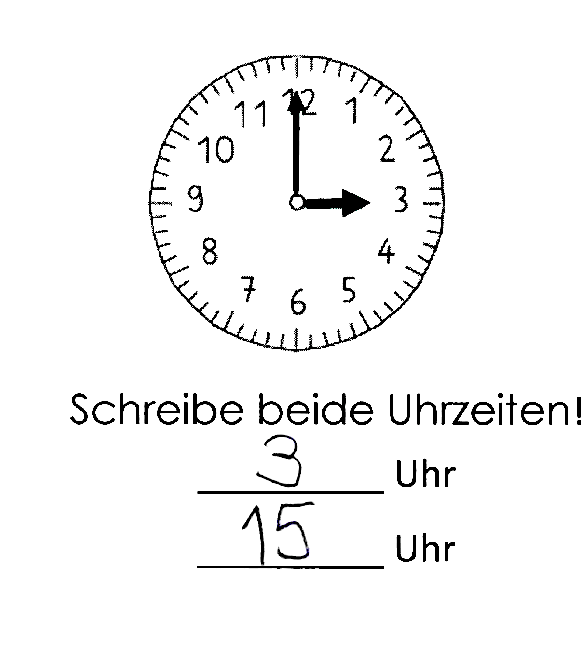 Aufgabenstellung: Schreibe beide Uhrzeiten.
Aufgabenstellung: Schreibe beide Uhrzeiten.
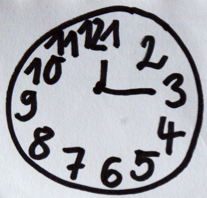 Aufgabenstellung: Zeichne eine Uhr, auf der es drei Uhr ist.
Aufgabenstellung: Zeichne eine Uhr, auf der es drei Uhr ist.
Jasemin kann zwar genau wie Philipp beide Uhrzeiten korrekt eintragen (Abbildung 3), jedoch kann man in ihrem Uhrenbild erkennen, dass sie noch nicht alle wesentlichen Merkmale einer Uhr beim Zeichnen der Uhr beachtet (Abbildung 4):
Die Eins steht oben in der Mitte des Ziffernblatts, außerdem wurden die Ziffern nicht im gleichen Abstand auf dem Ziffernblatt eingetragen. Auffällig ist weiterhin, dass Jasemin zwar unterscheidbare Zeiger einzeichnet, jedoch steht ihre Uhr nicht wie gefordert auf 3 Uhr.
Natürlich gibt auch die erste Bearbeitung Aufschluss über Jasemins Kompetenzen, so wissen wir, dass sie beide Uhrzeiten dem vorgegebenen Zeigerstand zuordnen kann, diese Information erhalten wir aus ihrer eigenen Zeichnung nicht.
Mit informativen Aufgaben, erfahren wir dennoch viel mehr über den individuellen Lernstand von Jasemin und können so besser Fördermaßnahmen ergreifen.
Wie durch die vorangegangenen Beispiele verdeutlicht, eignen sich insbesondere Eigenproduktionen, bei denen die Schülerinnen und Schüler selbst entscheiden können, wie sie vorgehen und/ oder wie sie ihr Vorgehen bzw. dessen Ergebnisse darstellen. Weitere Informationen zu Eigenproduktionen finden sie unter PIKAS: Fortbildungsmodul: Lernen auf eigenen Wegen – Eigenproduktionen.
Wie können informative Aufgaben gestaltet werden?
Eine informative Aufgabe ist als ein Impuls an die Schülerinnen und Schüler zu verstehen, vorhandene Kompetenzen schriftlich zu artikulieren.
Zielsetzung dabei ist es, mehr Informationen über Denkweisen oder Denkwege einzelner Kinder zu erhalten. Dies kann etwa in Form von Rechnungen, Texten, bildlichen Darstellungen usw. geschehen (vgl. Selter 2013).
Je nach Art der konkreten Informationen, die Sie über die Denkwege der Kinder erhalten wollen, kann jeweils einer der folgenden Aspekte im Mittelpunkt stehen (vgl. Selter, 2013; 2017, S. 142):
-
Zeigen von Kenntnissen (z.B. Kreuze alle Figuren an, die symmetrisch sind.)
-
Demonstration von Fertigkeiten (z.B. Zeichne einen Kreis mit dem Durchmesser 4 cm.)
-
Finden von Aufgaben mit vorgegeben Bedingungen (z.B. Schreibe fünf Malaufgaben mit dem Ergebnis 1000 auf.)
-
Beschreiben eigener Vorgehensweisen (z.B. Rechne 37+29 aus. Beschreibe deinen Rechenweg so, dass ein anderes Kind ihn verstehen kann.)
-
Artikulation von Vorstellungen (z.B. Erfinde eine Rechengeschichte zur Aufgabe 24–8=16.)
-
Beschreibung und/oder Begründunge von Auffälligkeiten (z.B. Erkläre, warum bei der Addition von zwei ungeraden Zahlen immer eine gerade Zahl herauskommt.)
-
Vergleichen von Anforderungen (z.B. Schreibe eine leichte und eine schwierige Aufgabe auf. Warum ist das eine leichte/schwierige Aufgabe?)
Das wesentliche Gestaltungskriterium informativer Aufgaben ist es also, die Aufgabe für eigene Lösungen zu öffnen, mehrere Antwortmöglichkeiten zuzulassen und Erklärungen einzufordern. Weiterhin sollten die Aufgaben grundsätzlich so gewählt werden, dass zumindest ein Teil der Aufgabe von allen Kindern gelöst bzw. bearbeitet werden kann (keine Alles-oder-Nichts-Aufgaben).
Sinnvolle Aufgabenauswahl treffen
Für den Einsatz von informativen Aufgaben und die Erhebung von Lernständen der Kinder ist eine sorgfältige und planvolle Aufgabenauswahl zentral. Die Art der Aufgaben hängt davon ab, was im Zusammenhang mit dem Unterricht erhoben werden soll, damit auf dieser Grundlage weitere Fördermaßnahmen auf individuellem Niveau eingeleitet werden können. Um Aufgaben passend zu wählen oder anzupassen ist es wertvoll, typische Strategien sowie typische Fehlermuster von Kindern zu kennen.
Ein Beispiel:
Typische Strategien und Fehlermuster beim schriftlichen Subtraktionsalgorithmus lassen sich ermitteln, wenn etwa Zahlenwerte so gewählt werden, dass Subtraktionsaufgaben mit und ohne Zehnerübergang gelöst werden müsse. So erhalten Sie tiefere Einblicke in das Operationsverständnis der Kinder, oder decken mögliche Schwierigkeiten auf (siehe z.B. KIRA: Informative Aufgaben).
Welche Rückschlüsse auf die Kompetenzen des Kindes können Sie erhalten?
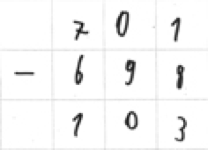 Thomas Lösung der Aufgabe (vgl. kira.dzlm.de)
Thomas Lösung der Aufgabe (vgl. kira.dzlm.de)
Sicher haben Sie den Fehler, den Thomas hier beim Rechnen gemacht hat, bemerkt.
Zunächst fällt auf, dass Thomas keinen Übertrag notiert, dies legt die Vermutung nahe, dass dies ein möglicher Grund für die fehlerhafte Bearbeitung ist. Bei der gewählten Aufgabe fallen jedoch zwei Überträge an, wovon er einen korrekt behandelt. Außerdem ist denkbar, dass ihm die Null im Minuenden Schwierigkeiten bereitet.
Spezifische Rückschlüsse über die Art der Schwierigkeiten können jedoch nicht gezogen werden. Eine erste praktikable Möglichkeit, Rückschlüsse auf mögliche Schwierigkeiten bei der Lösung zu erhalten, ist die Aufforderung: „Beschreibe wie du dabei vorgegangen bist!“ Dies kann sowohl schriftlich, also auch wie im Fall Thomas mündlich geschehen.
Thomas Bearbeitung der Aufgabe 701-698
Um auf eine mögliche Fehlerursache zu schließen, wurde Thomas gebeten, seinen Rechenweg zu erläutern. Aber wie im Video sichtbar wird, ist es auch durch die Befragung nicht immer möglich, die genaue Ursache für die fehlerhafte Bearbeitung eindeutig festzustellen.
Aufgabentypen informativer Aufgaben
In vielen Lehrwerken sind informative Aufgaben bisher eher selten zu finden, jedoch ist es bei nahezu jeder herkömmlichen Aufgabe möglich, diese in eine informative Aufgabe umzugestalten.
Idealtypisch gibt es vier Möglichkeiten Aufgaben so zu gestalten, dass sie mehr Informationen über die Denkweisen von Kindern preisgeben:
-
Aufgabenvariationen anbieten: Veränderung der Darstellung oder Situation kann bei Kindern bei der gleichen Grundaufgabe zu verschiedenen Vorgehensweisen führen.
 entnommen aus Hengartner & Röthlisberger 1999, S. 49
Im Beispiel wurde die Aufgabe 12:3 in zwei unterschiedlichen Kontexten angeboten. Das erste Bild zeigt eine Bild-Sach-Aufgabe und die zweite eine rein symbolische Darstellung der Aufgabe. Daniels Lösungen zeigen, dass er bei unterschiedlicher Darstellung der Aufgabe unterschiedliche Vorgehensweisen wählt.
entnommen aus Hengartner & Röthlisberger 1999, S. 49
Im Beispiel wurde die Aufgabe 12:3 in zwei unterschiedlichen Kontexten angeboten. Das erste Bild zeigt eine Bild-Sach-Aufgabe und die zweite eine rein symbolische Darstellung der Aufgabe. Daniels Lösungen zeigen, dass er bei unterschiedlicher Darstellung der Aufgabe unterschiedliche Vorgehensweisen wählt.
Es kann vorkommen, dass ein Kind eine Aufgabe lediglich in einem bestimmten Zusammenhang beherrscht bzw. seine Kompetenzen in anderen Kontexten nicht zeigen kann.
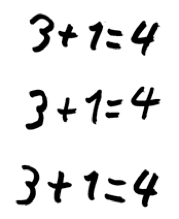 Daniels Lösung für Aufgabenteil 1 (bildliche Darstellung)
Daniels Lösung für Aufgabenteil 1 (bildliche Darstellung)
 Daniels Lösung für Aufgabenteil 2
Daher zeigt sich, dass das Angebot verschiedene Aufgabenvariationen (Darstellungen einer Aufgabe) mehr über die Kompetenzen des einzelnen Kindes preisgeben kann.
Daniels Lösung für Aufgabenteil 2
Daher zeigt sich, dass das Angebot verschiedene Aufgabenvariationen (Darstellungen einer Aufgabe) mehr über die Kompetenzen des einzelnen Kindes preisgeben kann.
-
Nebenrechnungen einfordern: Nebenrechnungen geben zusätzlich zu den Ergebnissen Einsicht in die Lösungswege und Fähigkeiten der Kinder.
-
 entnommen aus Sundermann & Selter 2006, S. 86 f.
entnommen aus Sundermann & Selter 2006, S. 86 f.
-
Vorgehensweisen darstellen lassen: Wenn man Kinder dazu auffordert, ihre Vorgehensweisen darzustellen, eröffnen sich häufig interessante Einblicke in ihre Denkwege.
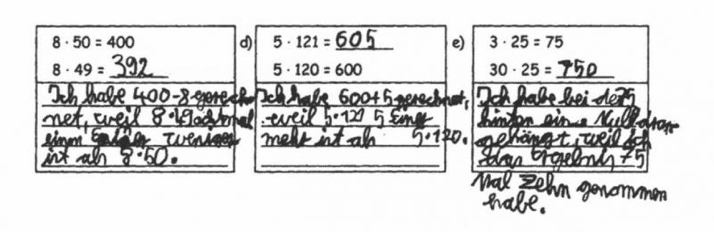 entnommen aus Sundermann & Selter 2006, S. 88
entnommen aus Sundermann & Selter 2006, S. 88
-
Zusammenhängende Aufgaben anbieten: Durch eine systematische Aufgabenzusammenstellung wird die Erhebung eines Fehlermusters erleichtert.
 Thomas Lösung der Aufgabe (vgl. kira.dzlm.de)
Einzelne, für sich alleinstehende Aufgaben, (vgl. Abbildung 5), die für sich genommen keinen hohen Informationsgehalt haben, werden durch eine systematische Zusammenstellung informativer.
Thomas Lösung der Aufgabe (vgl. kira.dzlm.de)
Einzelne, für sich alleinstehende Aufgaben, (vgl. Abbildung 5), die für sich genommen keinen hohen Informationsgehalt haben, werden durch eine systematische Zusammenstellung informativer.
Dazu werden anhand bestimmter Kriterien systematisch Aufgaben zusammengestellt, um beispielsweise Fehlermuster in der Bearbeitung von Aufgaben zu erhalten.
Mögliche Kriterien sind beispielsweise aufgabentypische Schwierigkeitsmerkmale (vgl. dazu Abschnitt 3) oder die Verwandtschaft von Aufgaben (z.B. 5·90, 90·5, 450:5, 4500:50 usw.).
Ergänzend zur Aufgabe 701-698 könnten Thomas folgende Aufgaben vorgelegt werden, in denen die Aufgabenmerkmale übernommen werden.

So enthält die Aufgabe 560-321, genau wie die erste Aufgabe (701-698), eine Null (aber an der Einer- anstatt der Zehnerstelle des Minuenden) und auch Überträge.
Die Aufgabe 607- 385 enthält genau wie die erste Aufgabe eine Null und Überträge. In der Aufgabe 687-305 ist die Null im Subtrahenden, Überträge fallen nicht an. Die Aufgabe 713 - 281 enthält keine Null, aber dafür wird ein Übertrag erforderlich.
Die Aufgabe 7068-6998 enthält die Null an der Hunderterstelle, ebenso fallen Überträge an.
Welche Aussagen können Sie nun über die vermuteten Fehlermuster treffen.
 Thomas Bearbeitung, typische Schwierigkeiten
Thomas Bearbeitung, typische Schwierigkeiten
An den weiteren Aufgabenbearbeitungen zeigt sich, dass die beiden aufgestellten Vermutungen nicht zutreffen. Thomas notiert zwar die Überträge nicht, dennoch löst er die weiteren Aufgaben korrekt. Ausnahme bildet die Aufgabe 7068 - 6998. Dort lässt sich tatsächlich das gleiche Fehlermuster wie bei 701 - 698 entdecken.
Welche besonderen Gemeinsamkeiten, die sie nicht mit den anderen Aufgaben teilen, weisen die Aufgaben 701 - 698 und 7068 - 6998 auf?
Thomas hat zwar keine generellen Schwierigkeiten mit der schriftlichen Subtraktion, da er viele Aufgaben korrekt löst.
Betrachtet man jedoch die beiden falsch gelösten Aufgaben genauer, fällt auf, dass Thomas lediglich Schwierigkeiten mit der Entbündelung hat, wenn von der Null entbündelt werden muss.
Während dies durch alleiniges Betrachten der Aufgabe 701 - 698 allerhöchstens eine wage Vermutung sein kann, liefert erst die Analyse der systematisch zusammengestellten Aufgaben begründete Hinweise (vgl. KIRA: Schriftliches Rechnen – Subtraktion)
Wie können informative Aufgaben genutzt werden, um individuelle Lernstände effizient und alltagstauglich zu erfassen?
Lernen ist ein Prozess, daher kann eine punktuelle Leistungsfeststellung etwa in Form von Klassenarbeiten den vielschichtigen Lernentwicklungen der Kinder nicht umfassend gerecht werden. Guter Mathematikunterricht stellt individuelle Lernstände kontinuierlich und stärkenorientiert fest und nutzt diese Grundlage für die Planung, Durchführung und Reflexion des Unterrichts. Doch wie können individuelle Lernstände effizient und alltagstauglich erfasst werden?
Neben den Standortbestimmungen bietet die Arbeit mit dem sogenannten Mathebriefkasten (PIKAS: Unterrichtsmodul: Leistung – Mathebriefkasten) eine Grundlage für eine kontinuierliche Wahrnehmung der individuellen Leistungen.
Zunächst einmal stellt sich die Frage: Was macht ein Briefkasten in meinem Mathematikunterricht?
Der Mathebriefkasten ist als Organisationsform zu betrachten, die der Arbeit im Unterricht gewisse Freiräume bietet. Für die Arbeit mit dem Mathebriefkasten werden informative Aufgaben, die individuelle Aufgabenbearbeitungen und Erklärungen beinhalten, genutzt, um regelmäßig (z.B. alle 2 Wochen) individuelle Denkweisen der Kinder zu erheben (vgl. Sundermann & Selter, 2011). Die Aufgaben werden auf kleinen Zetteln (z.B. A5 oder A6) angeboten, die nach der Bearbeitung in den Briefkasten eingeworfen werden sollen.
Wenn der Mathebriefkasten als festes Element in den Unterrichtsalltag eingebaut wird, liefert er ein authentisches Bild dessen, was das Kind leistet. „Zentral ist, dass es sich bei Mathebriefen nicht um eine Form von Lernzielkontrollen handelt, sondern um ein diagnostisches Instrument, das als Grundlage für die zielgerichtete Förderung der einzelnen Kinder bildet.“ (Selter 2013, S. 2).
Dabei ist es bedeutsam, den Kindern genau dieses Ziel transparent zu machen. Den Lernenden sollte klar sein, dass es sich bei den Diagnose- oder (Mathebriefkasten-)Aufgaben um eine Information für die Lehrkraft handelt, auf deren Grundlage der Unterricht bzw. die Förderung zielgerichtet und kindspezifisch angepasst wird (vgl. Selter 2017, S. 142).
Innerhalb der einzelnen Aufgaben, kann dies zum Beispiel mit folgender Aufforderung realisiert werden: „Erkläre so, dass ich verstehen kann, wie du gedacht hast!“ Dadurch wird den Kindern deutlich, dass es nicht allein um Lösungen, sondern um eine Hilfestellung für die Lehrperson zur weiteren Unterrichtsplanung geht.
Anregungen, wie Sie informative Aufgaben für den inklusiven Mathematikunterricht adaptieren können finden unter Mathe inklusiv.