Wir befinden uns am Anfang einer Stunde irgendwo in der Mitte einer Unterrichtseinheit zur halbschriftlichen Subtraktion. Die Kinder einer dritten Klasse versammeln sich im Sitzhalbkreis vor dem "heißen Stuhl", neben dem ein Notenständer steht, auf dem Rechenwege angeheftet werden können. Wer auf dem "heißen Stuhl" Platz nimmt, darf seinen Rechenweg vor- bzw. zur Diskussion stellen oder zum ausgestellten Rechenweg einen Kommentar abgeben, während die anderen Kinder schon gespannt davor sitzen und warten.
In der nun geschilderten Einführungsphase ging es um die Aufgabe 403-397 aus der Vorstunde. Die Lehrperson hatte dazu einige Kinder gebeten, ihre Rechenwege aus der Vorstunde zu präsentieren. Neben diversen anderen Kindern meldeten sich Julia und Paul, um ihre individuellen Lösungen vorzustellen.
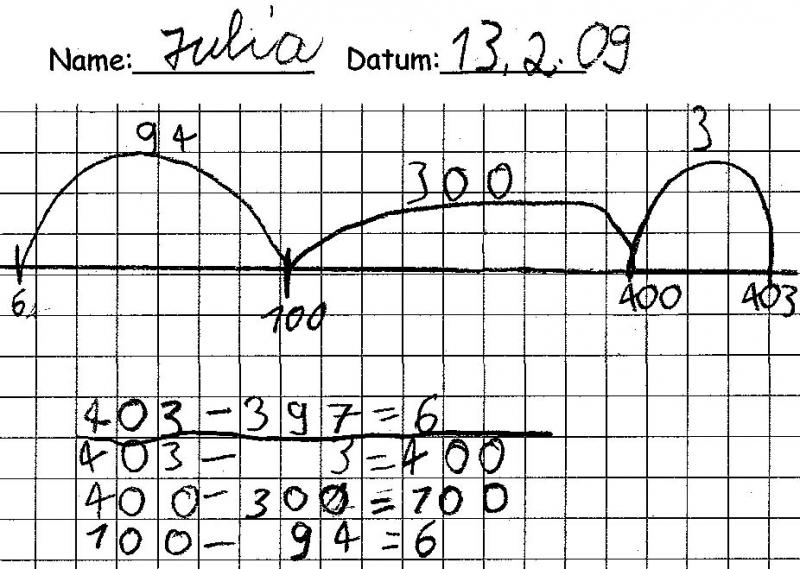
Nachdem Julia ihren Rechenweg zur Diskussion gestellt hatte, erkannten und erläuterten ihre Mitschüler, dass Julia von 403 ausgehend rückwärts gerechnet hatte, dabei die 397 (aus ihrer Sicht) geschickt in Portionen zerteilte, die das Rechnen erleichterten:
Zunächst minus 3, um auf dem glatten Hunderter zu landen, dann volle 300 zurück, was einfach war, und dann "den Rest", also noch 94 von der 100 abgezogen, um zum Ergebnis 6 zu gelangen. Dabei musste sie im Kopf bei der Zerlegung des Subtrahenden mitrechnen, um "den Rest" von 94 bestimmen zu können.
An dieser Stelle regte die Lehrkraft an, dass es möglicherweise eine gute Idee sein könne, die Zahlen geschickt zu zerlegen, um glatte Zwischenzahlen zu bekommen.
Die Fragen, die sich hier aufdrängen, sind die folgenden:
Mit welchem (langfristigen) Unterrichtsziel lässt die Lehrperson die Kinder ihre unterschiedlichen Lösungswege vorstellen?
Warum sollen die anderen Kinder erklären, wie Julia gerechnet hat? Warum kommentiert die Lehrperson diese Strategie als "durchaus geschickt"?
Wie kann man also der Lösungsvielfalt bzw. den individuellen Lösungswegen der Schülerinnen und Schüler im Mathematikunterricht Raum geben, aber am Ende dennoch die von der Fachdidaktik und dem Lehrplan avisierten Rechenstrategien und -verfahren zielgerichtet in einem offeneren Unterricht erreichen?
Eine Organisation des Unterrichts im Sinne der "fortschreitenden Mathematisierung" - auch "Ich-Du-Wir-Prinzip" genannt - bietet hier einen möglichen Lösungsansatz.
Um dieses Prinzip näher zu erläutern, werden auf dieser Seiten folgende Punkte konkretsieret:
Gewiss werden Sie erkannt haben, dass es im obigen Beispiel um das "Rechnen auf eigenen Wegen" geht, und darum, die Lernenden selbst aktiv den Zugang zum Unterrichtsgegenstand gehen zu lassen. Es geht also eben nicht um die Einführung eines Standardweges, der dann bis zur Geläufigkeit geübt wird, bevor der nächst schwierigere Standardweg durchgearbeitet werden darf.
Neben dem Prinzip des aktiv-entdeckenden Lernens kommen bei dem hier vorgestellten Weg noch mindestens ein weiteres für das Lernen im Mathematikunterricht als zentral gehaltenes didaktisches Prinzip zum Tragen (vgl. Krauthausen & Scherer 2007, S. 122): Das "Prinzip der Fortschreitenden Mathematisierung" (auch "fortschreitende Schematisierung" genannt), auf das nun etwas genauer eingegangen werden soll, immer auf das im Einstieg beschriebene Unterrrichtsbeispiel bezogen.
Der niederländische Mathematikdidaktiker Adri Treffers kann als Ideenvater dieses Prinzips bezeichnet werden, weil er diesen Begriff in der mathematikdidaktischen Gemeinschaft etabliert hat (Treffers 1983). Doch was bedeutet das Prinzip der Fortschreitenden Mathematisierung?
Es wird gefordert, dass die Kinder im Unterricht die Gelegenheit bekommen sollen, umfangreiche Zahlhandlungen zunehmend zu schematisieren, zu verkürzen und zu verinnerlichen (vgl. Treffers 1983). Diese Aussage muss man natürlich im damaligen Kontext sehen und auf die heutige Didaktik anpassen. Wir verstehen darunter zunächst vielleicht umständlich anmutende, individuelle Rechenwege, wie Julia sie probiert, die dann immer eleganter werden. Letztlich soll erreicht werden, dass die Standardstrategien der halbschriftlichen Subtraktion durch "zunehmendes Schematisieren, Verkürzen und Verinnerlichen" als flexible Rechenstrategien in der Klasse etabliert werden (vgl. Treffers 1983).
Idealtypischer Verlauf von Unterrichtseinheiten nach Treffers
Die im Einstieg beschriebene Unterrichtsstunde stellt nur eine Momentaufnahme in Verlauf der Unterrichtsreihe zur halbschriftlichen Subtraktion dar. Treffers selbst hat einen idealtypischen Verlauf von Unterrichtseinheiten, die im Sinne der Fortschreitenden Mathematisierung/Schematisierung aufgebaut sind, beschrieben (vgl. Kasten 1).
T1. "Zwangloser" Einstieg in das Thema
T2. Kontextaufgaben: Bedeutungsvolle Rechenhandlungen
T3. Anknüpfen an informelle Rechenmethoden der Kinder, Anregung der Anwendung geeigneter(er) Methoden
T4. Von Anfang an "große Zahlen", Differenzierung durch "Lösungsstufen"
T5. "Schriftliches Rechnen wird mit Kunstgriffrechnen verknüpft"
T6. Immer stärkere Verkürzung und Schematisierung
T7. "Die Dauer des Lehrgangs kann von Schüler zu Schüler variieren"
T8. "Das erstrebte Endziel braucht nicht für alle Schüler übereinzustimmen"
Der Einstieg in die halbschriftliche Subtraktion im Tausenderraum wurde durch einen für die Kinder bedeutsamen Kontext gewählt: Ein Bild von einem örtlichen Großkino regte die Kinder zum Erzählen an. Ein Foto von einem Kinosaal ließ die Vermutung hervorrufen, wie viele Menschen dort wohl Platz nehmen könnten, und der eigentliche Einstieg in den Kontext war die Aufgabe: "Im Kino sitzen 346 Leute. 187 kommen noch dazu". Hierzu sollten sich die Kinder zeichnerisch, rechnerisch und berichtend schriftlich äußern. Ausgehend von ihren Lernvoraussetzungen konnten die Kinder also ihren Rechenweg und die Notationsweise zunächst selbst bestimmten, analog zu den Trefferschen Unterrichtsabschnitten T1, T2 und T4.
Als Anknüpfung an die Addition wurden bei den Kindern das Rechnen am Rechenstrich und der Versuch der analogen halbschriftlichen Notation als "geeignetere" Methode angeregt (T3) - frei nach dem Motto "Wer sich die einzelnen Rechenschritte am Rechenstrich bereits im Kopf vorstellen kann und wem das Zeichnen des Rechenstrichs zu aufwändig ist, kann seine Rechnungen auch halbschriftlich notieren". Ebenso wurden exemplarisch besonders geschickt erscheinende Rechenwege der Kinder ausgewählt, um weitere "geeignetere Methoden" bei den anderen Kindern anzuregen (T3). Alle Rechnungen fanden zunächst an den realen Zahlenwerten des echten Kinos statt (T4). Zudem wurden von der Lehrkraft Aufgaben hinzugefügt, die bestimmte, geschickte Strategien geradezu provozieren (so wird man z.B. bei der Aufgabe 509 - 492 nahezu "gezwungen" ergänzend zu rechnen, weil Minuend und Subtrahend so nah beieinander liegen).
Unter "Schriftliches Rechnen wird mit Kunstgriffrechnen verknüpft" (T5) versteht Treffers die zunehmende Verknüpfung informeller Schülerdokumente in "schriftlicher" Form mit immer eleganteren "Rechentricks". Dabei handelt es sich nicht etwa um "Rechentricks", die der Lehrer verrät oder vorgibt, sondern um von Wissenden (Didaktikern, Lehrkäften) als effizienter erkannte Rechenstrategien.
Diese Rechenstrategien werden dabei nicht einzeln vom Lehrer eingeführt und von den Schülerinnen und Schülern Stunde für Stunde durchexerziert und auswendig gelernt, sondern sie dienen vor allem der Lehrkraft als Hintergrundwissen und Diagnosewerkzeug beim Interpretieren der Schülerlösungen und beim Anregen "geschickterer" Strategien sowie bei der Einführung von Bezeichnungen für bestimmte Strategien. Nach mehreren Stunden des Anregens und Fortschreitens gelangen die Kinder zu neuen Rechenstrategien (T6). Somit erfolgt nach jeder individuellen Arbeitsphase ("So rechne ICH."), ein Austausch mit den anderen Kindern ("Wie rechnest DU?"). Dadurch entsteht ein großes Repertoire an Rechenstrategien, das von allen Kindern der Klasse zunehmend genutzt werden sollte ("So rechnen WIR!"). Daher wird dieses Unterrichtsprinzip auch als das "Ich-Du-Wir" Prinzip bezeichnet.
Bleiben noch die letzten beiden, nicht unwichtigen Unterrichtsabschnitte nach Treffers (T7, T8): Auch im gegebenen Beispiel war es so, dass die Kinder unterschiedlich schnell und unterschiedlich weit beim Erwerb halbschriftlicher Subtraktionsstrategien fortschritten. So gelang es einer Schülerin erst nach mehreren Unterrichtsstunden die Fehlvorstellung, die schriftliche Addition einfach auf die schriftliche Subtraktion zu übertragen (dann aber, wenn Überträge entstanden, einfach größere minus kleinere Zahl zu rechnen), zu überwinden, und am Ende über den Rechenstrich zum halbwegs sicheren Beherrschen der Strategie "Schrittweise" zu kommen. Andere Schüler hingegen haben sich zu "Motoren der Entwicklung" der anderen gemacht, eine neue Idee nach der anderen produziert und damit andere Kinder in ihrer Entwicklung angeregt, wie die folgenden Beispiele zur Analyse zeigen.
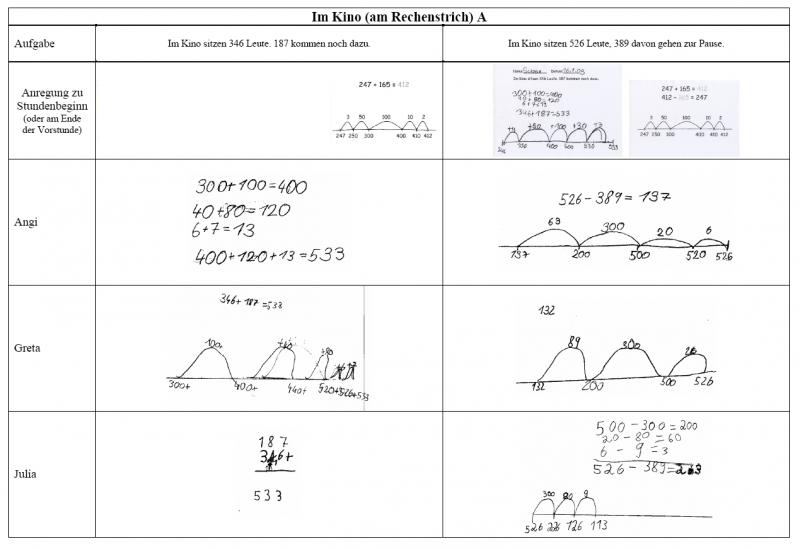
Betrachten Sie exemplarisch nur drei Kinder aus der oben beschriebenen Unterrichtseinheit (klicken Sie hierzu auf das unten dargestellte Bild). Die Tabelle ist so aufgebaut, dass in der Zeile "Aufgabe" zu sehen ist, welche Aufgabe bzw. Aufgaben die Kinder aktuell in der Stunde bearbeiten sollten. In der Zeile darunter befinden sich Anregungen, die die Kinder vorher bekommen haben (z.B. Rechenstrategien ihrer Mitschüler oder auch Aufgabenblätter zur Weiterarbeit). Darunter sehen Sie, wie die Kinder mit der jeweiligen Aufgabe bzw. den jeweiligen Aufgaben umgegangen sind und inwiefern sie die Anregungen aufgegriffen haben
Eigenaktivität
Betrachten Sie die Dokumente der drei Kinder (klicken Sie dazu auf das obige Bild) unter folgenden Gesichtspunkten:
1. Inwiefern greifen die Kinder die zu Stundenbeginn gemachten Anregungen auf? Sehen Sie also, dass die Kinder aus der Wir-Phase etwas für ihr individuelles Rechnen übernommen haben?
2. Wie entwickeln sich die Rechenstrategien und Notationen der einzelnen Kinder im Zuge der Einheit? Wo sehen Sie, dass das Kind seine Notationen verkürzt (weniger Rechenschritte, nicht mehr am anschaulichen Rechenstrich) und neue Strategien nutzt?
(Tipp: Drucken Sie sich die Dokumente zur Analyse aus und legen Sie die einzelnen Blätter zum Vergleich nebeneinander!)
Hier sehen Sie weitere Kinderdokumente, die Sie mit den gleichen Analysefragen wie in 3. betrachten sollen.
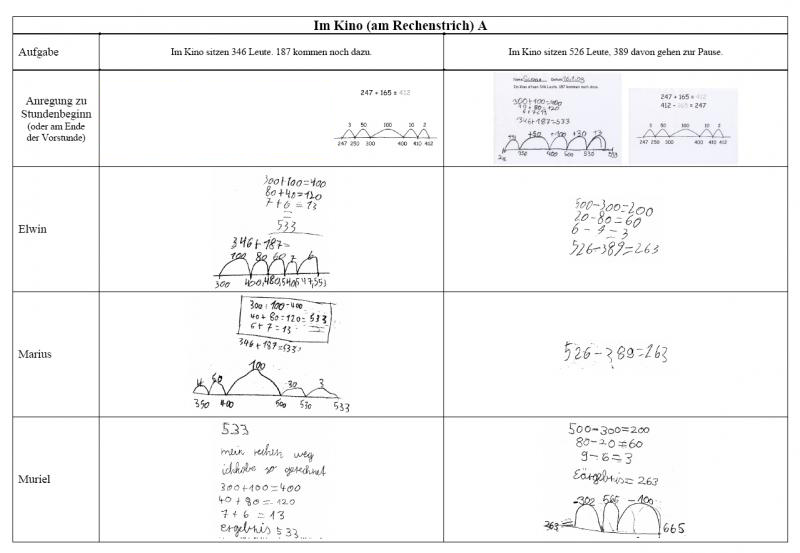
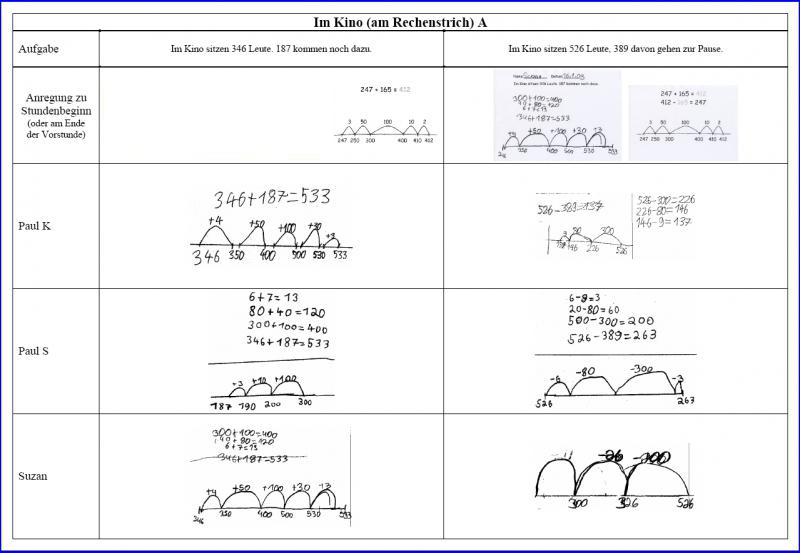
Aus dieser Vielzahl der Dokumente wird deutlich, dass die Kinder sich durchaus entwickeln, aber sehr individuell. Jede neue, verkürzte Notation und jeder neue Rechenweg wurde von den Kinder vorher wohl durchdacht und sehr bewusst in das eigene Repertoire an Rechenstrategien übernommen. Durch dieses Vorgehen kann erreicht werden, dass die langsameren Kinder ihre Rechenwege wirklich verstehen und mit Verständnis neue Rechenwege vorsichtig ausprobieren können, während schnellere Kinder aus einer Vielzahl an Strategien wählen und über die Geschicktheit ihrer Rechenwege nachdenken sollen.
Auf unserer Partnerprojektseite KIRA finde Sie im Kontext derr fortschreitenden Mathematisierung ein Beispiel zum Halbschirftlichen Rechnen.
KIRA: Halbschriftliche Subtraktion
Bei der fortschreitenden Mathematisierung spielt der Weg vom Konkreten zum Abstrakten eine große Rolle, weshalb der behutsame und sinnvolle
Einsatz von Material an dieser Stelle ebenfalls thematisiert werden sollte. Wie bereits erwähnt wurde, bietet die Selbstlernplattform des Projektes
PriMakom („Primarstufe Mathematik kompakt“) hierzu interessante Hintergrundinformationen sowie hilfreiche Unterrichtsbeispiele an. Die Plattform richtet sich insbesondere an Lehrerinnen und Lehrer, die Mathematik fachfremd unterrichten und sich somit mathematikdidaktische Kenntnisse in kompakter Form rasch aneignen möchten. Selbstverständlich sind auch Lehrpersonen mit einer fundierten mathematischen Ausbildung, Lehramtsanwärter sowie Studierende dazu eingeladen, die Homepage zu besuchen.