Ähnlich wie zahlreiche andere Aufgabenformate (beispielhaft mehr dazu auf den Seiten Zahlenmauern und Zahlenketten), bieten die Rechendreiecke (Wittmann & Müller 2000, S. 56 f.) zahlreiche Möglichkeiten, um inhalts- und prozessbezogene Kompetenzen gleichzeitig zu fördern (vgl. Kultusministerium NRW 2009). Werden die Rechendreiecke (oder andere Aufgabenformate) „nur“ zum Rechnen und eben nicht zum Entdecken genutzt, wird das Potential dieser Aufgaben nicht ausgeschöpft. Die Kinder sollen dazu angeleitet werden, mathematische Muster zu entdecken und diese beschreiben sowie begründen zu können.
Wie das gelingen kann und das Potential inhalts- sowie prozessbezogene Kompetenzen zeitgleich zu fördern ausgeschöpft wird, werden auf der Hintergrundseite folgende Schwerpunkte bearbeitet:
Ausgangspunkt zur Nutzung der Rechendreiecke im obigen Sinne, ist die Erforschung der ihnen zugrundeliegenden mathematischen Strukturen (zunächst durch die Lehrkraft und dann auch – auf einem anderen Niveau – durch die Kinder). Um die mathematischen Strukturen zu erforschen, bietet sich das Rechnen einiger Aufgaben an. Beispielhaft wird hier der Fokus auf die Außensumme der Rechendreiecke gelegt.
Eigenaktivität
Rechnen Sie die folgenden Rechendreiecke aus. Berechnen Sie jeweils die Summe der Außenzahlen. Was fällt Ihnen auf? Warum ist das so?
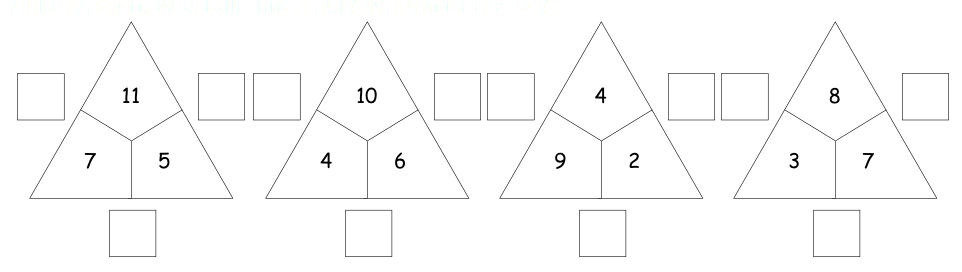
Beweis der geraden Außensumme
Durch die Eigenaktivität konnte die Vermutung aufgestellt werden, dass die Außensumme von Rechendreiecken immer gerade ist. Um dies zu zeigen, stellen Sie sich vor, sie packen eine bestimmte Anzahl von Plättchen in ein gelbes Säckchen – dieses soll nun für die obere Innenzahl stehen. Eine (andere) beliebige Anzahl an Plättchen legen Sie in ein blaues Säckchen, welches für die linke Innenzahl steht. Genauso verfahren Sie mit einem – hier grünen – weiteren Säckchen für die rechte Innenzahl.
Da die Summe der oberen und der linken Innenzahl die linke Außenzahl ergeben, wird diese dann durch je ein blaues und ein gelbes Säckchen repräsentiert. Diese Veranschaulichung eignet sich auch schon in der Grundschule, um die Kinder zum Verallgemeinern anzuregen. Ein Variablenverständnis kann so angebahnt werden.
Dieselbe Vorgehensweise lässt sich auch auf Variablen übertragen. So setzen wir einfach die obere Innenzahl als a, die linke als b und die rechte als c fest in diesem Beispiel. Das ist sicherlich nichts mehr, das so mit Grundschulkindern thematisiert wird. Aber gerade um mathematische Strukturen zu verdeutlichen, eignet sich eine algebraische Herangehensweise an dieses Aufgabenformat.
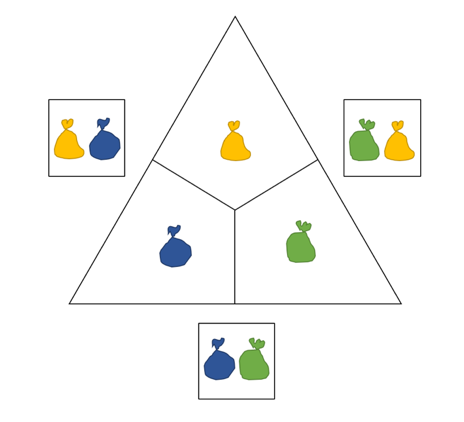Grundschulgemäße Verallgemeinerung
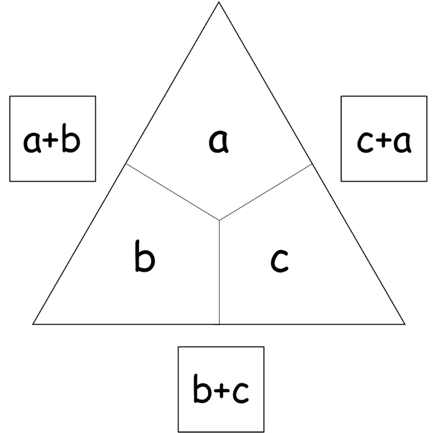Algebraische Verallgemeinerung
Wenn Sie nun also alle Außenzahlen zusammenfassen, um deren Summe zu erhalten, ergibt sich folgendes Bild:
Sortiert man dies ein wenig um, sieht man, dass alle drei Säckchen je zweimal vorkommen:
Daraus lässt sich nun auch folgern, warum alle Außensummen gerade sind. Egal, ob beispielsweise in dem gelben Säckchen eine gerade oder ungerade Anzahl liegt, da es zwei gelbe sind, ergibt sich eine gerade Zahl. Somit ergeben sich in der Säckchendarstellung 3 Gruppen – also die gelben, die blauen sowie die grünen Säckchen – die alle gerade sind, da es immer zwei sind. Addiert man nun alle drei, ergibt sich auch in jedem Fall eine gerade Zahl. Mathematisch zeigt sich das durch die 2 vor der Klammer – egal welche drei Innenzahlen Sie addieren, diese werden verdoppelt und so ergibt sich eine gerade Zahl in der Außensumme.
Auch das sollte nach Möglichkeit sprachlich unterstützt werden. Sicherlich sind die Säckchen eine visuelle Unterstützung für die Kinder, können aber nicht alleine ohne Sprache stehen und verstanden werden. Dazu finden Sie im Unterricht einen Wortspeichervorschlag.
Erst nach der mathematischen Durchdringung durch die Lehrkraft und der Herausarbeitung der Strukturen kann das Aufgabenformat nun optimal genutzt werden. Hier zeigt sich zum Beispiel wie beschrieben, dass eine Heranführung an die Außensumme in Verbindung mit geraden und ungeraden Zahlen sich besonders anbietet, um den Kindern Entdeckungen in diesem Bereich zu ermöglichen. Thematisiert man also gerade und ungerade Zahlen, bietet sich eine Überschneidung mit den Rechendreiecken an.
Das Entdecken, Beschreiben und Begründen zählen immer mehr zu den wichtigen Kompetenzen des zeitgemäßen Mathematikunterrichts der Grundschule. Um diese Begründungen auch nachvollziehen und bewerten und rückmelden zu können, ist es aber eben auch wichtig, dass die mathematischen Strukturen vorab durchdrungen worden sind. Unter Berücksichtigung dieses Wissens lassen sich dann zahlreiche weitere Aufgabenstellungen ableiten, bei denen Ihre Schülerinnen und Schüler zum Entdecken, Beschreiben und Begründen von mathematischen Zusammenhängen angeregt werden. Weitere Anregungen dazu erhalten Sie auf der nächsten Seite im Unterricht.
Mit diesem Aufgabenformat lassen sich viele prozessbezogenen Kompetenzen fördern (siehe auch Problemlösen verlinken), die sich beispielsweise durch die Strukturen ableiten. Beim Problemlösen ist es wichtig Aufgaben zu nutzen, für die Schülerinnen und Schüler noch keine Routinefähigkeiten ausgebildet haben.
Eigenaktivität
Lösen Sie dieses Rechendreieck. Wie gehen Sie vor?
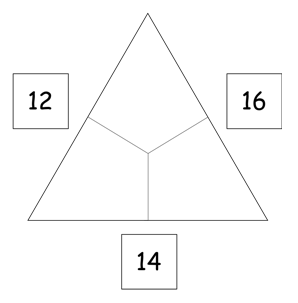
Wenn Sie sich an das Eingangsbeispiel zurückerinnern, hat sich Luis hier der Herausforderung gestellt, das Rechendreieck zu lösen, bei dem alle drei Außenzahlen aber keine Innenzahl gegeben war.
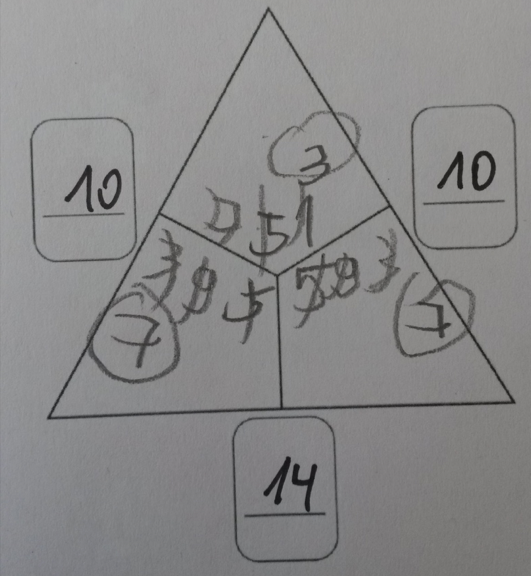
Wenn Sie die Lösung von Luis noch einmal genauer betrachten, sieht man, dass bereits ganz viel hinter seiner Lösung steckt. Einige Versuche werden unternommen, um auf die richtige Lösung des Rechendreiecks zu kommen. Es wurde vermutlich zuerst einer der oberen Außenzahlen in 5 und 5 aufgeteilt, dabei wurde aber deutlich, dass sich so die 14 nicht erreichen lässt, da nun unten auch 10 erreicht wurde.
Anschließend nutzt Luis eine andere Zerlegung der 10 in 1 und 9, um die untere Summe zu vergrößern. Auch das trägt er mit der zweiten 9 wieder ein und sieht nun aber, dass die Summe dann 18 und somit zu groß wäre. Nun nähert er sich der richtigen Lösung weiterhin, indem er Zerlegungen der 10 nutzt. Luis entwickelt also auch Strategien, um die Aufgabe zu lösen. Die Veränderungen die er vornimmt scheinen systematischer zu werden.
Um im Sinne des Spiralprinzips auf das Vorwissen der Kinder aufzubauen und trag- und anschlussfähige Vorstellungen für das Weiterlernen aufzubauen, ist eine Anleitung zum Verallgemeinern ihrer Entdeckungen ein wichtiger Punkt – auch schon in der Grundschule.
Das soll nicht heißen, dass Variablen in der Grundschule eingeführt werden sollen, sondern viel mehr, dass die Kinder anhand der Zahlenbeispiele und mit Unterstützung von Material angeleitet werden, ihre Aussagen zu verallgemeinern. So zeigt Akinwunmi (2012) beispielsweise, dass Kinder das durchaus schon beherrschen, indem sie ein oder mehrere Beispiele angeben, oder sprachlich verallgemeinere Elemente nutzen („Es ist immer gerade bei der Außensumme“).
Aber auch die Darstellung mit den Säckchen ist eine für Kinder zugängliche und verständliche Möglichkeit Zusammenhänge zu verdeutlichen. Wenn mit den Kindern besprochen wird, dass in ein Säckchen beliebig viele Plättchen gesteckt werden, können die Kinder mit kleinen Säckchen – als erste Repräsentanten einer x-beliebigen Zahl – umgehen. Die unterschiedlichen Farben dienen dabei der Unterscheidung der Variablen.
