Eigenaktivität
Wir starten mit einem kleinen Selbstversuch: Übersetzen Sie bitte die Zahlen von 1 bis 20 in das Alphabet – also die 1 in das A, die 2 in das B und so weiter... Rechnen Sie nun bitte die folgenden Aufgaben.
E + F =
E + G =
I + K =
J + J =
Haben Sie sich während des Lösungsprozesses beobachtet? Vermutlich haben Sie zwischendurch die Finger zur Hilfe genommen, um sich die Position der Buchstaben nochmal zu vergegenwärtigen. Sie waren dann in der Lage von Kindern, die zählend und damit mühsam und fehleranfällig Ergebnisse von Aufgaben wie 5 + 6, 5 + 7, 9 + 11 oder 10 + 10 ermitteln.
Vielleicht haben Sie aber auch das Ergebnis von E + G aus dem Ergebnis der Aufgabe E + F abgeleitet, da G im Alphabet um 1 hinter F liegt. Oder Sie haben das Resultat von I + K genutzt, um das Ergebnis von J + J zu erzielen – I liegt direkt vor J und K liegt direkt hinter J, beide Aufgaben führen demnach zum selben Resultat.
Dann waren Sie in der Lage von Kindern, die nicht-zählend rechnen und die Ergebnisse von Aufgaben aus denen von anderen Aufgaben ableiten, die sie schon kennen bzw. ermittelt haben: 5 +7 ist 1 mehr als 5 + 6, 9 + 11 hat das selbe Resultat wie 10 + 10.
Zu Beginn der Schulzeit ist zählendes Rechnen – häufig mit Hilfe der Finger – für nicht wenige Kinder eine ganz normale Vorgehensweise, um Additions- oder Subtraktionsaufgaben zu lösen. Das ist kein Wunder, denn die Finger sind das erste Rechenhilfsmittel, das die Kinder zudem immer bei sich tragen. Für Schulanfänger ist die Zahlenreihe manchmal nicht mehr als eine Art Gedicht, welches sie auswendig aufsagen können.
Im Laufe des ersten Schuljahres überwinden die meisten Kinder das zählende Rechnen und entwickeln ein immer tragfähigeres Verständnis von Zahlen und Operationen. Sie begreifen zunehmend, dass Zahlen nicht nur eine Position in einer Reihe haben, sondern auch dass sie aus anderen Zahlen zusammengesetzt sind.
Doch manche Kinder bleiben beim zählenden Rechnen, auch über den Zahlenraum bis 20 hinaus. Sie ermitteln dann das Resultat von 35 + 17 mit Hilfe ihrer Finger – ein langwieriger, fehleranfälliger Prozess. Solches verfestigtes zählendes Rechnen gilt als ein Hauptmerkmal von besonderen Schwierigkeiten beim Rechnen.
Schwierigkeiten im Lernprozess sind ganz normal. Erst, wenn diese Schwierigkeiten umfangreich und dauerhaft auftreten, kann man von besonderen Rechenschwierigkeiten sprechen, im Weiteren lassen wir das Attribut ‚besondere‘ aus Gründen der besseren Lesbarkeit weg. Doch was sind Rechenschwierigkeiten?
Eine von allen, die sich mit diesem Thema befassen, akzeptierte Definition von Rechenschwierigkeiten existiert nicht. Dafür sind sowohl die Ausprägungsformen und Ausprägungsgrade bei jedem Kind als auch die Hintergrundtheorien und Forschungstraditionen zu unterschiedlich.
Um besser verstehen zu können, worauf man im Unterricht achten sollte, um Rechenschwierigkeiten zu erkennen oder besser noch: zu verhindern, werden häufig zentrale Merkmale formuliert. Dabei ist wichtig zu erwähnen, dass ein Kind, was ein Merkmal aufweist, nicht zwingend rechenschwach ist. Vielmehr sind typischerweise einige der Merkmale bei rechenschwachen Kindern in unterschiedlichen Ausprägungsformen zu erkennen.
In Anlehnung an Schipper (2011) und Wartha & Schulz (2014) können vier zentrale Merkmale identifiziert werden, die Rechenschwierigkeiten ausmachen.
Nicht tragfähiges Zahlverständnis
Die Grundlage allen Rechnens bildet ein tragfähiges Zahlverständnis. Es kann als ein Merkmal von Schwierigkeiten in Mathematik gelten, wenn die Lernenden Zahlen nicht mit Bedeutungen verknüpfen, verschiedene Darstellungsformen nicht miteinander vernetzen und den vorhandenen Beziehungsreichtum von Zahlen für das Weiterlernen nicht nutzen können.
Paula beispielsweise ordnet noch nicht jedem Zahlwort ein Objekt zu, sondern jeder gesprochenen Silbe.

Nicht tragfähiges Operationsverständnis
Analog zum Zahlverständnis kann es als Anzeichen nicht tragfähigen Operationsverständnisses gelten, wenn Lernende Rechenoperationen nicht mit Bedeutungen verknüpfen, verschiedene Darstellungsformen nicht miteinander vernetzen und den vorhandenen Beziehungsreichtum von Zahlen und Aufgaben für das Weiterlernen nicht nutzen können.
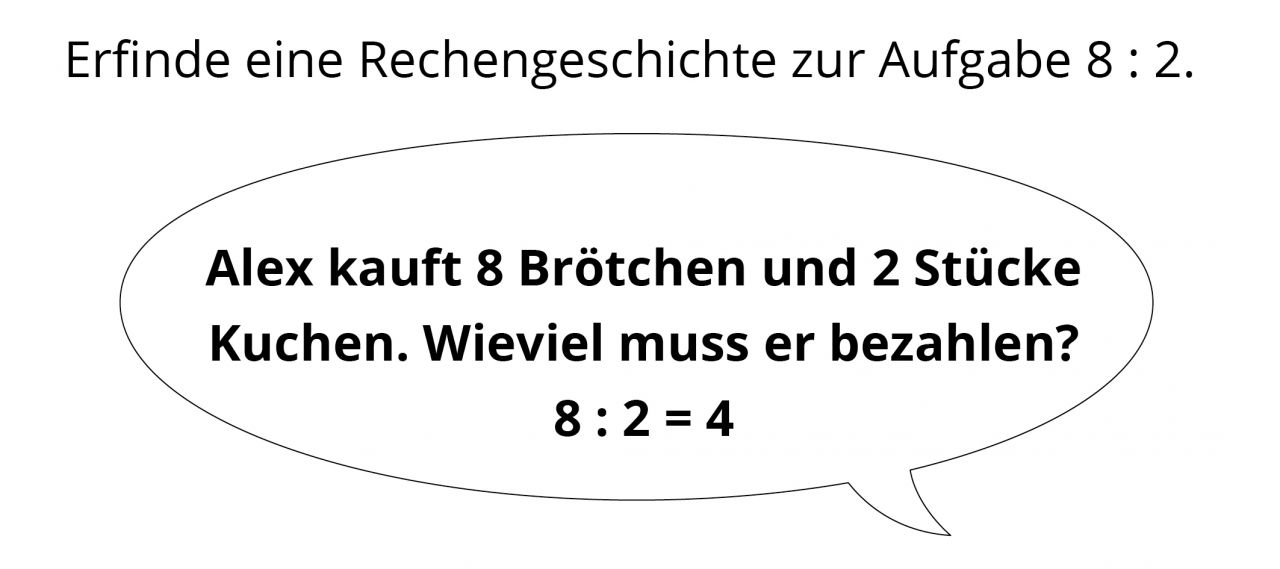
Tim beispielsweise formuliert keine im Sinne des weiterführenden Lernens passende Aufgabe, auch wenn er das richtige Resultat angibt.
Nicht tragfähiges Stellenwertverständnis
Zu verstehen, dass Anzahlen fortgesetzt gebündelt werden, um sie mit nur wenigen Ziffern oder mit Material übersichtlich darstellen zu können, gehört zu den zentralen Ideen unseres Zahlsystems. Lernende müssen verstehen, dass die 3 in 35 etwas anderes bedeutet als die 3 in 307 oder 83.
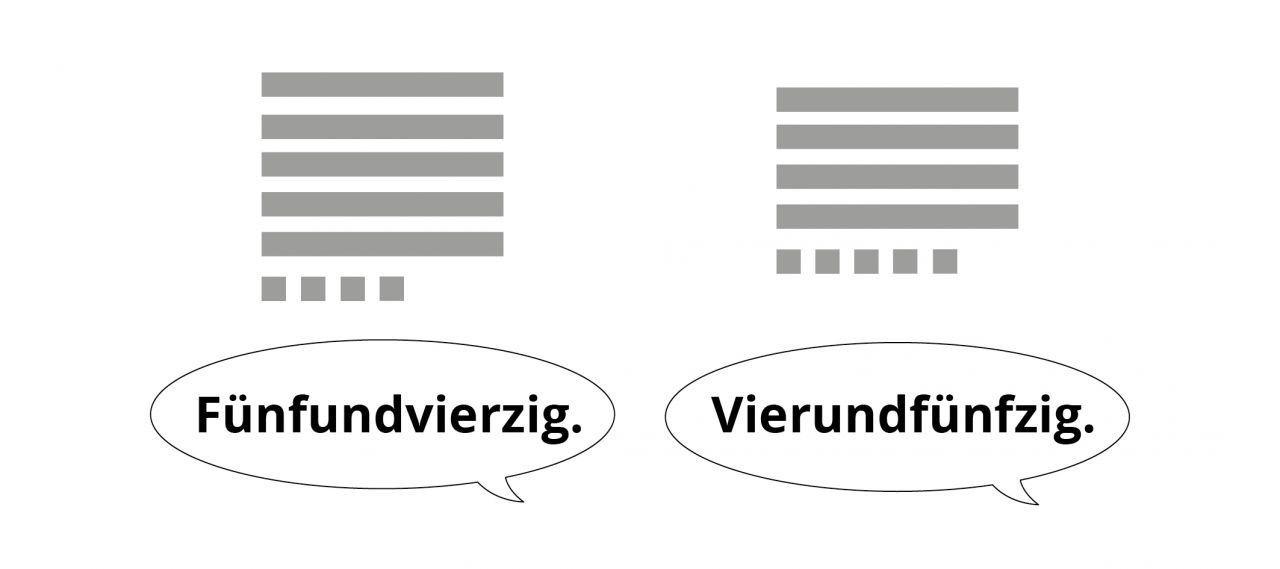
Mehmet beispielsweise hat noch Schwierigkeiten damit, dass im Deutschen zuerst die Einer und dann die Zehner gesprochen werden und kann daher noch nicht zu vorgelegten Darstellungen das passende Zahlwort nennen.
Verfestigung des zählenden Rechnens
Zählendes Rechnen ist in frühen Phasen des Lernprozesses normal. Dass beispielsweise Schulanfängerinnen und Schulanfänger die Aufgabe 3 + 4 lösen, indem sie mit Material oder an ihren eigenen Fingern zunächst bis 3 und dann von dort aus um 4 weiter zählen (4, 5, 6, 7), ist keineswegs unüblich. Im weiteren Verlauf des Lernprozesses sollten die Kinder das zählende Rechnen nicht länger als Lösungsmethode verwenden.
Diese notwendige Entwicklung betrifft nicht nur das Einspluseins und das Einsminuseins, sondern das gesamte Rechnen, wie z. B. auch das additive Rechnen in größeren Zahlräumen oder das Einmaleins und Einsdurcheins.
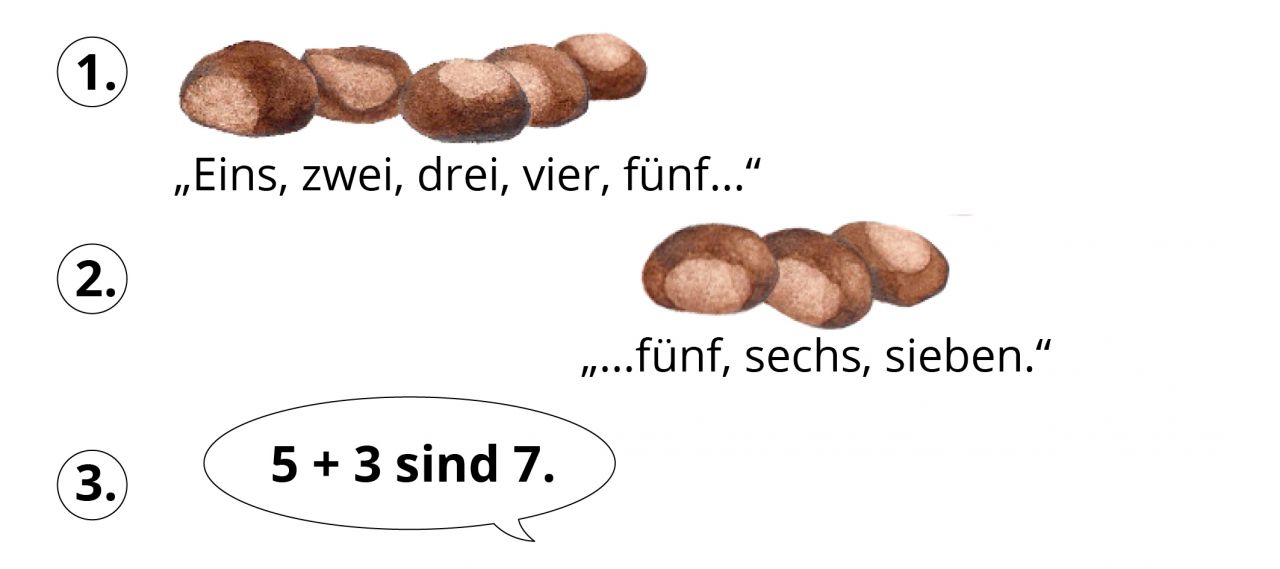
Leah beispielsweise ermittelt das Ergebnis von 6 + 3, in dem sie beide Summanden korrekt hinlegt und jede Kastanie einzeln abzählt. Dabei begeht sie den Fehler, nicht bei 6, sondern bei 5 weiter zu zählen.
Weitere Merkmale wie Unsicherheiten in der Raum-Lage-Wahrnehmung, Links-rechts-Verwechselungen, fehlende Größenvorstellungen, schwaches auditives Gedächtnis oder geringes Selbstvertrauen können ebenfalls auftreten.
Die vier hier genauer beschriebenen Merkmale verweisen auf stoffliche Hürden, die Lernende im Verlauf der Grundschulzeit überspringen müssen.
Wie die Schülerinnen und Schüler dabei durch Lehrpersonen unterstützt werden können, beschreibt die vom Ministerium für Schule und Bildung herausgegebene und von Mitgliedern des Projekts PIKAS geschriebene Handreichung: ‚Rechenschwierigkeiten vermeiden. Hintergrundwissen und Unterrichtsanregungen für die Schuleingangsphase‘, erhältlich beim Aufruf von PIKAS: Selbststudiumsmodul: 'Rechenschwierigkeiten - Handreichung'.
Weitere Hinweise
Zahlverständnis
Zahlvorstellungen erwerben
PIKAS: Zahlvorstellungen (ZR 0 bis 100)
Mathe sicher können: Diagnose- und Fördermaterial, Module N1 und N2
Operationsverständnis
Operationsverständnis aufbauen
KIRA: Über welche Operationsvorstellungen Kinder verfügen
Mathe sicher können: Diagnose- und Fördermaterial, Module N3 und N4
Stellenwertverständnis
PIKAS: Entwicklung des Stellenwertverständnisses
Stellenwertverständnis
Mathe sicher können: Diagnose- und Fördermaterial, Module N1 und N2
Nicht-zählendes Rechnen
Kopfrechnen
PIKAS: 1+1 richtig üben
PIKAS: Erarbeitung nicht-zählender Rechenstrategien
Ablösung vom zählenden Rechnen
Mathe sicher können: Diagnose- und Fördermaterial, Module N5 und N6
PIKAS: 1–1 richtig üben
KIRA: Schülerlösungen zur Multiplikation und Division
PIKAS: Einmaleinslernen auf eigenen Wegen