Unterricht

Üben mit Material im Unterricht

In Bezug auf die im Einstieg dargestellte Situation ist es also wichtig, nicht das formale Auswendiglernen in den Vordergrund zu stellen, sondern die zugrundeliegenden Materialhandlungen, die sowohl konkret als auch später im Kopf stattfinden sollen. Dies sollte auch insbesondere den Eltern deutlich gemacht werden, die auf eine schnelle Automatisierung drängen (z.B. im Rahmen eines Elternabends oder durch einen Elternbrief).

Wie kann ein solcher Materialeinsatz nun konkret im Unterricht aussehen?

Im Folgenden sollen unterrichtspraktische Anregungen für die Gestaltung von gestützten Übungsprozessen aufgezeigt werden.
Als inhaltliches Beispiel wird hier die Einführung und das anschließende Festigen und Üben der Multiplikation am Hunderterpunktefeld in der 2. Klasse genutzt.

Sie finden dazu Erläuterungen zu folgenden Punkten:

• Darstellung von Aufgaben am Punktefeld
• Knackpunkte beim konkreten Einsatz des Materials
• Übungsmatrix konkret für das gestütze Üben des 1·1
• Das Vierphasenmodell am Beispiel der Multiplikation am Punktefeld

Darstellung von Aufgaben

Bei der Multiplikation können drei Grundvorstellungen unterschieden werden (Padberg & Benz 2011, S. 128-131):

• zeitlich-sukzessive Handlungen (also eine Handlung mehrmals hintereinander durchführen, z.B. 3 mal 2 Flaschen Wasser aus dem Keller holen),
• räumlich-simultane Anordnungen (z.B. ein Blumenbeet aus 3 Reihen mit jeweils 20 Blumen) und
• kombinatorischer Kontext (z.B. die Anzahl der Möglichkeiten, die sich aus Kombination von 3 Hosen mit 4 Pullovern ergibt).

Das Punktefeld zeigt dabei die räumlich-simultane Anordnung.

Durch einen sogenannten „Malwinkel“ können dann auf dem Hunderterpunktefeld einzelne Multiplikationsaufgaben dargestellt werden, wobei die nicht zur Aufgabe gehörenden Plättchen mithilfe des Winkels abgedeckt werden und somit der Fokus auf die Aufgabe gerichtet wird. Dabei wird das schnelle Erfassen der Aufgabe und der Anzahl der Plättchen durch die Fünferunterteilung unterstützt. Diese macht auch das Zerlegen in leichtere Teilaufgaben (z.B. 3·8 in 3·5 + 3·3 mithilfe des Distributivgesetzes) einfacher und sichtbar.

Eigenaktivität

Stellen Sie die Aufgabe 6·7 am Punktefeld dar und überlegen Sie sich verschiedene Möglichkeiten zur Berechnung (z. B. mithilfe von Kernaufgaben wie 2·x, 5·x und 10·x oder anderen leichteren Aufgaben wie Verdopplungsaufgaben), die aus dem entstandenen Bild ablesbar sind (vgl. dazu PIKAS: Haus 3: Infopapier).
Wie kann das Material dabei helfen, die Aufgabe leichter zu lösen?

Kommentar zur Eigenaktivität

Die Aufgabe 6·7 kann so dargestellt werden mit dem Malwinkel, dass 6 Zeilen mit jeweils 7 Punkten zu sehen sind. Das Material unterstützt durch die Darstellung und die Fünferunterteilung die Strukturierung der Aufgabe.
Die Fünferunterteilung hilft dabei, kleinere, leichter zu rechnende Aufgaben (Kernaufgaben) zu sehen. Auch eine fortgesetzte Addition ist in der Darstellung am Punktefeld sichtbar, wenn die einzelnen Reihen nacheinander betrachtet werden.
Berechnen kann man die Aufgabe z.B.

und auch durch abzählen, ggf. in Schritten (was allerdings langwierig und fehleranfällig und daher langfristig nicht tragfähig ist.

Knackpunkte beim konkreten Einsatz des Materials

Wichtig beim Einsatz des Materials ist die Einführung und gemeinsame Besprechung mit den Kindern. Hierbei sollte sowohl deutlich werden, wie man den Malwinkel auf das Punktefeld legen kann, als auch mögliche verschiedene Sichtweisen (vgl. auch Eigenaktivität).
Den Kindern sollte deutlich werden, dass das Material nicht nur als Lösungshilfe für die Schwachen, sondern als Kommunikationsmittel für alle genutzt werden soll. Schnelle Kinder können innerhalb der Phasen ggf. schneller voranschreiten, jedoch sollten keine Phasen übersprungen werden.
Die Rückführung auf die mentale Vorstellung des Materials sollte immer wieder betont werden, was besonders durch die Verbalisierung der Handlungen erreicht wird.
Die Materialhandlungen können sowohl am großen Demo-Material an der Tafel oder am Overheadprojektor, als auch zeitgleich mit der ganzen Klasse, wobei jedes Kind selbst am seinem Material arbeitet, durchgeführt werden.
Insbesondere dem Üben mit einem Partner kommt durch die damit verbundene Verbalisierung der Handlungeneine große Bedeutung zu. Aufgabenstellungen dazu könnten lauten:

• Wie legst du den Malwinkel an?
• Wie viele Zeilen / Wie viele Spalten hat das sichtbare Punktefeld?
• Welche Kernaufgaben / leichtere Aufgaben kannst du zur Berechnung der Aufgabe nutzen?

Das abschließende Ziel ist es, dass Bilder des Materials im Kopf entstehen, in diesem Fall also des Punktefeldes und dass die Kinder Beziehungen zwischen 1·1-Aufgaben kennen und nutzen, um die Ergebnisse möglichst schnell abrufen bzw. berechnen zu können.

Übungsmatrix konkret für das gestützte Üben des 1·1

In diesem Abschnitt sollen nun noch einmal genauere Aufgabenstellungen vorgestellt werden, wobei das gestützte Üben im Sinne der Übungsmatrix (siehe Hintergrund) im Vordergrund steht.
Als Einstieg in die Multiplikation bieten sich zunächst gestützte bzw. anschauliche und unstrukturierte Aufgaben an (Feld 1 der Übungsmatrix), also das Legen bzw. Visualisieren von Einzelbeispielen am Punktefeld mit dem Malwinkel. Hierzu wird eine bestimmte Aufgabe gelegt und in Teilaufgaben zerlegt (s. Kommentar Eigenaktivität).
Dies kann sowohl durch Zeigen, farbliches Markieren oder auch durch Umkreisen der Punkte geschehen. Wichtig dabei ist in jedem Fall die konkrete Handlung. Jedes Kind sollte also ein Punktefeld mit einem Malwinkel zur Verfügung haben.
Hier ein mögliches Beispiel von unserem Partnerprojekt Mathe sicher können: N4 - Multiplikation und Division verstehen(vgl. Akinwunmi, Deutscher und Selter 2014, S. 42):

Mögliche Impulse der Lehrkraft können dabei sein:

• Welche Mal-Aufgabe siehst du hier? Findest du noch eine andere Mal-Aufgabe, die man auch sehen kann? Erkläre, wie du die Aufgabe siehst.
• Finde die Kernaufgaben in den Darstellungen der „großen“ Aufgaben und kreise diese ein.
• Wie kann man die Aufgabe möglichst geschickt ausrechnen?
• Bei welchen Teilen des Punktefeldes kannst du die Anzahlen direkt erkennen? (z.B. durch Nutzung der Fünferstruktur)

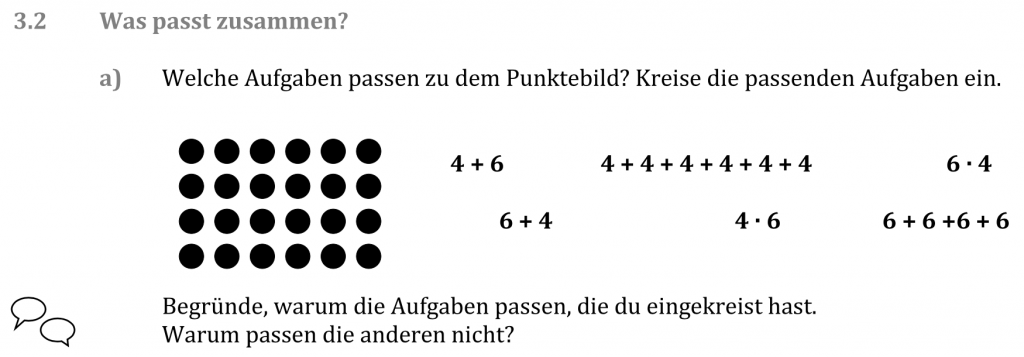
Als weitere Aufgabenstellung können die Kinder begründen, welche der vorgegebenen Aufgaben zu dem entsprechenden Punktefeld passen (vgl. Akinwunmi, Deutscher & Selter 2014, S. 43). Dabei können Sie als Lehrkraft besonderes Augenmerk auf angemessene Fachsprache legen (Zeile/Reihe, Spalte, jeweils x Reihen mit y Punkten...) (siehe auch Sprachförderung).

Ist den Kindern der Umgang mit dem Malwinkel und dem Punktefeld geläufig, können Sie als weitere Übung strukturierte und gestützte Aufgaben stellen (Feld 2 der Übungsmatrix). Hierbei handelt es sich dann nicht mehr um Einzelaufgaben, sondern um jeweils mehrere, zusammenhängende Aufgaben, wobei die Beziehung der Aufgaben untereinander im Vordergrund stehen sollte.
Eine mögliche Aufgabenstellung finden Sie hier (vgl. Akinwunmi, Deutscher und Selter 2014, S. 43):

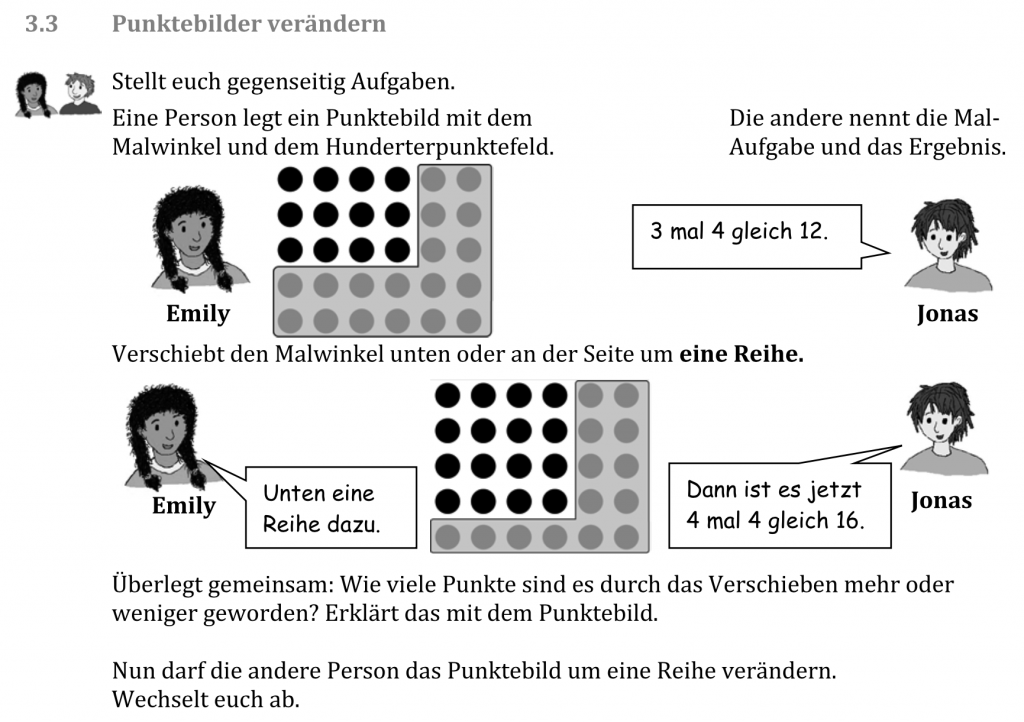
Mögliche Impulse der Lehrkraft sowie passende Erweiterungen können sein:

• Wie kann man aus 7·8 die Aufgabe 7·9 machen? Beschreibe, was du tun musst.
• Aus 5·7 mach 6·7. In welche Richtung verschiebt sich der Malwinkel?
• Lege und zeichne alle Aufgaben mit 7 Punkten in einer Reihe.

Vierphasenmodell am Beispiel der Multiplikation am Punktefeld

Alle oben vorgestellten Aufgaben können und sollten im Sinne des Vierphasenmodells (vgl. Hintergrund) entsprechend mehrfach auf verschiedenen Ebenen durchgeführt und ggf. erweitert werden, so dass die Kinder nicht nur konkret am Material handeln, sondern das Material zunehmend mental im Kopf verwenden. Auf jedem Feld der Übungsmatrix kann also der Ablösungsprozess vom konkreten Handeln stattfinden und die Vorstellung der Handlung rückt in den Vordergrund.
Die Phasen können innerhalb des Unterrichts bei derselben Aufgabenstellung nacheinander thematisiert werden. Auch ein Zurückspringen zu einer vorherigen Phase ist möglich und insbesondere bei Schwierigkeiten sinnvoll.
Die hier vorgestellten Erläuterungen beziehen sich auf das oben genannte erste Beispiel (Feld 1 der Übungsmatrix: Malaufgaben am Punktefeld legen und berechnen).

1. Arbeiten an geeignetem Material

Beispiel zur Aufgabe 6·9: Die Kinder legen den Malwinkel so auf das Punktefeld, dass ein Punktefeld mit 6 Reihen mit je 9 Punkten sichtbar bleibt. Dabei wird die sprachliche Beschreibung gefordert („Ich habe 6 Reihen mit je 9 Punkten.“). Anschließend beschreibt das Kind die Zerlegung in leichtere Kernaufgaben, um damit das Ergebnis zu berechnen.
Hierbei gibt es verschiedene Möglichkeiten (z.B. „Ich rechne 6 Reihen mit 5 Punkten, das sind 30, dann noch 6 mal 4 Punkte, das sind 24 Punkte, sind zusammen 54 Punkte. Also ist 6·9=54.“).

2. Nutzen des Materials ohne konkretes Handeln

Die Kinder haben das Punktefeld vor sich liegen und haben somit Sicht aufs Material, allerdings wird die Aufgabe nicht mehr konkret mit dem Malwinkel gelegt. Die Aufgabe wird beschrieben (siehe 1.) und wiederum über die Zerlegung in leichtere Kernaufgaben gelöst.

3. Nutzen des Materials ohne Sicht darauf

Das Kind beschreibt der Lehrkraft oder einem anderen Kind das Bild, was sich auf dem Punktefeld mit dem Malwinkel ergibt. Die Zerlegung in Kernaufgaben findet in der Vorstellung statt, der Partner kontrolliert die Erklärungen am Punktefeld. Wichtig dabei ist, dass nur der Partner das konkrete Material sehen kann.
Umgekehrt kann der Partner hinter einem Sichtschirm auch eine Aufgabe mit dem Malwinkel legen und beschreiben, wie das entstandene Bild aussieht. Das Kind findet die Aufgabe heraus und berechnet sie unter Zuhilfenahme von leichteren Kernaufgaben.

4. Nutzen des Materials in der Vorstellung

Nun können Aufgaben gestellt werden und das Kind nennt die passenden Kernaufgaben und das Endergebnis, wobei das Punktefeld in der Vorstellung genutzt werden sollte. Auch die umgekehrte Variante (passende Kernaufgaben werden genannt, Kind nennt die „große“ Aufgabe) ist denkbar, außerdem auch das Rechnen von Malaufgaben auf Zeit.
Die Kinder könnten auch mit zwei Würfeln würfeln und dann die entsprechende Malaufgabe und die zugehörige Vorstellung am Material erläutern. Bei Schwierigkeiten sollte die Vorstellung der Kinder aktiviert werden durch geeignete Nachfragen (z.B. „Wie sieht das zugehörige Bild am Punktefeld aus?“, „Wie viele Punkte-Reihen gibt es?“, „Wie viele Punkte sind in einer Reihe?“).
Auch oben vorgestellte strukturierte und gestützte Aufgaben (Feld 2 der Übungsmatrix: Beziehungen zwischen Aufgaben nutzen) können im Sinne des Vierphasenmodells nach und nach von der konkreten zur mentalen Handlung hin genutzt werden, um das innere Vorstellungsbild aufzubauen.
Fortsetzbar ist die Arbeit mit dem Hunderterpunktefeld anschließend z.B. durch das Vierhunderterpunktefeld, bei welchem dann Aufgaben bis 20·20 dargestellt werden können. Werden später noch größere Multiplikationsaufgaben gerechnet, kann immer wieder auf die Vorstellung der Punktefelder verwiesen werden.
Weiteres Material finden Sie z.B. auf unserer Partnerseite Mathe sicher können: N6 B - Ich kann sicher multiplizieren und meine Rechenwege erklären