Inhaltliches Verständnis durch Üben mit Material
In den Bildungsstandards im Bereich „Zahlen und Operationen“ findet sich folgende Kompetenzanforderung:
Die Kinder sollen am Ende der vierten Jahrgangsstufe „die Grundaufgaben des Kopfrechnens (Einspluseins, Einmaleins, Zahlzerlegungen) gedächtnismäßig beherrschen, deren Umkehrungen sicher ableiten und diese Grundkenntnisse auf analoge Aufgaben in größeren Zahlenräumen übertragen [und] mündliche und halbschriftliche Rechenstrategien verstehen und bei geeigneten Aufgaben anwenden“ (KMK 2004, S. 9).
Um solche Aufgaben auswendig beherrschen zu können, müssen diese geübt werden. Doch ein reines Auswendiglernen ohne die Nutzung von Aufgabenzusammenhängen und ohne Einsatz von Material ist langfristig nicht ergiebig (siehe auch Kopfrechnen).
Warum sollte Üben mit Material gestützt werden?
Im Folgenden finden Sie Erläuterungen zu folgenden Punkten:
Definition von Üben
Beim Üben werden „Wissenselemente oder eine Fertigkeit (...) anhand einer größeren Zahl gleichartiger Aufgaben wiederholt angewandt“ (Wittmann 1992, S. 179). Das wiederholte Anwenden bedeutet allerdings nicht, dass dabei nicht nachgedacht werden sollte und die Anwendung sofort automatisiert passiert. Das Auswendiglernen zur schnellen Verfügbarkeit, z.B. beim 1x1, ist zwar eines der langfristig verfolgten Ziele, jedoch sollen Kinder zunächst verständnisbasiertes Wissen über Aufgaben und die Zusammenhänge erwerben, was durch eine vorschnelle Automatisierung oft nicht gelingt.
Das Üben ist ein Prozess, der Grundvorstellungen aufbauen und festigen soll durch die Anknüpfung an die Vorstellungen der Kinder. Damit ist unter Üben mehr zu verstehen als nur Wiederholen von bereits eingeführtem Stoff.
„Üben ist damit im Wesentlichen das Wiederaufnehmen eines (entdeckenden) Lernprozesses, das Nocheinmalnachbilden, Nocheinmaleinbauen von Lernsituationen“ (Winter 1984, S. 10).
Sehr wichtig dabei ist das Verständnis des Lernstoffes und die Vernetzung mit dem vorhandenen, eigenen Wissen, nicht das mechanische Abrufenkönnen von Einzelfakten.
Üben wird hier demnach als mehrschrittiger Lernprozess dargestellt. Jede Phase des Übungsprozesses ist durch die jeweils unterschiedliche Zielsetzung zentral auf dem Weg zur Automatisierung. Der Aufbau von Grundvorstellungen und allgemein eines gesicherten Operationsverständnisses müssen vorausgehen, bevor die Kinder überhaupt Zahlbeziehungen, Muster und Strukturen und Gesetzmäßigkeiten in formalen Rechenaufgaben erkennen, nutzen und übertragen können.
Insbesondere hat hier der Einsatz von Darstellungen und Materialien eine wichtige Funktion, um Vorstellungsbilder aufzubauen und die Strukturen und operative Veränderungen auch zu visualisieren. Und erst, wenn diese Vernetzung und Vertiefung angeregt wurde, kann eine Ablösung vom Material erfolgen, und die Lerninhalte können automatisiert werden.
Weiteres zum Thema Üben finden Sie auf der Primakom-Website ,,Üben".
Übungsmatrix
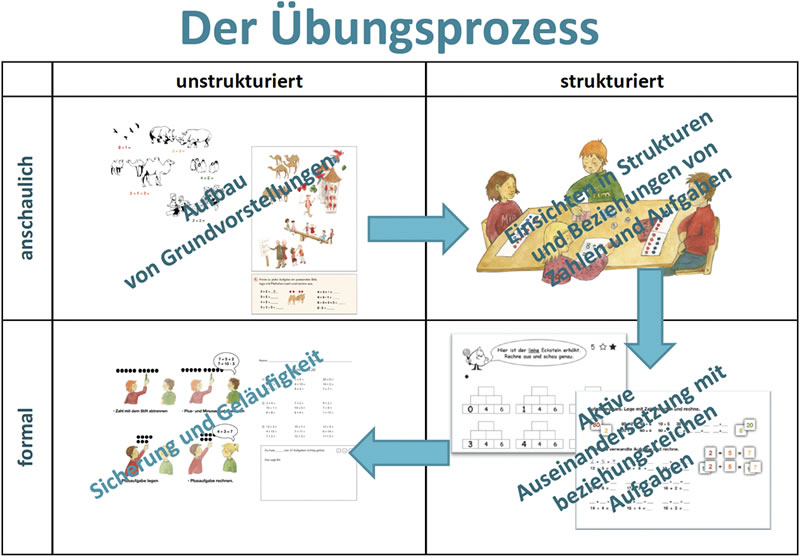
Der Übungsprozess kann in verschiedene Übungstypen untergliedert werden, die übersichtlich in einer Tabelle dargestellt werden können (siehe unten).
Zum einen wird dabei der Grad der Strukturierung unterschieden. Die Aufgaben einer Übungsserie können entweder einzeln willkürlich ausgewählt sein (unstrukturiert) oder sie stehen in einem ganzheitlichen Strukturzusammenhang und sind daher aufeinander bezogen (strukturiert). Zum anderen kann die Darstellungsform unterschieden werden in Aufgaben, die sich auf Anschauungsmaterial und Handlungen am Material stützen (gestützt bzw. anschaulich) und Aufgaben, die auf der rein symbolischen Ebene bearbeitet werden (formal bzw. ungestützt) (vgl. Wittmann 1992, S. 179).
Durch die Kombination der Möglichkeiten ergibt sich eine sogenannte Übungsmatrix:
 Übungsmatrix
Übungsmatrix
Übungsmatrix
Im ersten Teil des Übungsprozesses sollen Grundvorstellungen aufgebaut werden, anschaulich und unstrukturiert an Einzelbeispielen (Feld 1).
Anschließend soll dieses Wissen vernetzt und vertieft werden (Feld 2). Dies geschieht sinnvollerweise durch strukturiertes Üben mit Material und durch anschauliche Einsichten in Strukturen und Beziehungen von Zahlen und Aufgaben. Diese werden durch das Material erst möglich und sichtbar gemacht. Die zugrundeliegenden Strukturen werden bewusst und sichtbar gemacht, Entdeckungen sind möglich.
Nach den gestützten Phasen kann das strukturierte Üben ohne Material zum Vernetzen und Vertiefen auf formaler Ebene hilfreich sein (Feld 3). Hier setzen sich die Kinder aktiv mit Beziehungen zwischen den Aufgaben auseinander.
Erst abschließend kommt es zum formalen, unstrukturierten Üben (Feld 4), dem klassischen „Auswendiglernen“ von Einzelaufgaben bzw. Wissenselementen, die aber zur Sicherung der Geläufigkeit mehr als Abschluss und Abprüfen des Übungserfolges eingesetzt werden sollten.
Eigenaktivität
Überlegen Sie sich für jedes Feld der Übungsmatrix eine Übungsaufgabenstellung zum Thema „Kleines 1-1“.
Materialeinsatz beim Üben
Mathematiklernen ist ein Abstraktionsprozess. Handlungen sollen von den Kindern zunächst durchgeführt und dann verinnerlicht und im Geiste nachvollzogen werden. Langfristiges Ziel allen Arbeitens mit Material ist, dass die Kinder sich nach und nach vom Material lösen und die Rechenoperationen "im Kopf" lösen können.
Zum gestützten Üben gehört ein geeignetes Material. Bei der Auswahl des Materials sollte auf didaktische Kriterien geachtet werden. Genaueres dazu finden Sie im Materialteil.
Insbesondere beim Üben sollte darauf geachtet werden, dass die durchzuführenden Handlungen am Material strukturgleich zur angestrebten Vorstellung im Kopf sind (für konkrete Beispiele siehe Unterricht). Die Ausbildung von Vorstellungsbildern im Kopf und das mentale, nur vorgestellte Operieren mit dem entsprechenden Material sollte ohne ein „Umlernen“ möglich sein, so dass beispielsweise am Material nicht immer in Einerschritten operiert werden sollte, wenn später im Kopf größere Schritte durchgeführt werden sollen.
Weiterhin soll das Material die Verfestigung des zählenden Rechnens vermeiden helfen bzw. die Ablösung vom zählenden und den Übergang zum denkenden Rechnen unterstützen. Auch sollte es verschiedene individuelle Bearbeitungs- und Lösungswege zu ein und derselben Aufgabe ermöglichen und die Ausbildung flexibler Rechenstrategien unterstützen.
Weiterhin sollte das Material Übertragungen in eine von den Schülern zeichenbare Form gestatten.
Die Materialauswahl sollte gezielt stattfinden, um nicht zu viele verschiedene Materialien einzusetzen, da dies jeweils zusätzlichen Lernstoff bedeutet. „Außerdem ist zu beachten, dass der Lernerfolg nicht mit der Masse der Materialien, sondern mit der Reichhaltigkeit und Intensität der Schüleraktivitäten steigt“ (Wittmann & Müller 1990, S. 8.).
Rolle des Materials im Lernprozess
Um Material zweckmäßig einzusetzen, ist es sinnvoll, dies in mehreren Phasen zu tun, so dass die Handlung vom konkreten Material nach und nach im Kopf und nicht mehr auf der konkreten Handlungsebene stattfindet. Dadurch kann das Kind später auf die „mentale Vorstellung“ des Materials zurückgreifen.
Der Prozess vom konkreten zum gedanklichen Handeln wird durch das Vierphasenmodell zum Aufbau von Grundvorstellungen von Wartha und Schulz (2014) gut dargestellt.
Phase 1: Handlung am Material
Die Rechenoperation wird zunächst am Material konkret handelnd ausgeführt und vom Kind sprachlich begleitet. Die Versprachlichung der Handlung und der mathematischen Symbole ist dabei zentral.
Phase 2: Beschreibung der Handlung am Material mit Sicht auf das Material
Die zu lösende Aufgabe wird anfänglich nur mit dem Material gelegt und das Kind beschreibt und diktiert einem Partner, wie es zur Lösung kommt. Das Kind handelt also nicht mehr selbst, sondern kontrolliert den Handlungsprozess des Partners.
Phase 3: Beschreibung der Handlung ohne Sicht auf das Material
In dieser Phase beschreibt das Kind die gesamte Aufgabe ohne Sicht auf das Material, wobei die Handlung von einem Partner (für das Kind nicht sichtbar) noch durchgeführt wird.
Phase 4: Ausführen der Handlung in der Vorstellung
Zuletzt sollte sich das Kind die Aufgabe nur noch vorstellen und muss die gesamte Handlung mental am vorgestellten Objekt ausführen und beschreiben.
(vgl. Wartha/Schulz 2014, S. 63)
Ziel des Vierphasenmodells ist es, die durch das Darstellungsmittel (didaktisches Material) erzeugten Bilder zu verinnerlichen, damit sie später zum Rechnen im Kopf abrufbar sind und das Kind ohne Hilfsmittel im Kopf, mithilfe der in der Vorstellung entstandenen Bilder, rechnen kann und seine Vorstellung auch den Aufgaben anpassen kann.
Wichtig ist dabei nicht nur die Handlungserfahrung selbst, sondern auch das Sprechen darüber und die Versprachlichung der Handlung. Dieser Darstellungswechsel zwischen Sprache, Symbol und Handlung am Material hilft, tieferes Verständnis aufzubauen.
„Gerade das bildliche und sprachliche Darstellen von mathematischen Beziehungen hilft dahinterliegende Vorstellungen bewusst(er), sichtbar und kommunizierbar zu machen, mögliche Fehlvorstellungen aufzudecken und neue Vorstellungen in das eigene Wissensnetz einzubauen“ (Kuhnke 2012, S. 7).
Die Aufgaben der Lehrkraft bei der Umsetzung des Vierphasenmodells sind neben der Auswahl des geeigneten Materials die Beobachtung der Schülerhandlung und dabei die Aufforderung zur geeigneten Versprachlichung der Handlung. Weiterhin achtet sie darauf, dass das erarbeitete Handlungsvokabular auch eingesetzt und in den fortgeschrittenen Phasen immer der Bezug zur konkreten Handlung hergestellt wird. Außerdem ist es wichtig, einen besonderen Fokus auf die Phasen 2 und 3 zu setzen und diese nicht zu überspringen (vgl. Wartha & Schulz 2014, S. 64).
Umgesetzt werden kann dies durch Impulse wie
-
„Welche Aufgabe passt zu der Handlung/ dem Bild?“
-
„Erkläre, wie du vorgehst.“
-
„Welcher Schritt kommt als erstes? Was passiert danach?“
-
„Kannst du mehrere passende Aufgaben sehen?“
-
„Was musst du tun, wenn die Aufgabe größer werden soll?“
-
„Begründe, warum die Aufgaben passen?
Darstellungsmittel können daher als „Instrument des Erkennens“, aber auch als „Instrument des Kommunizierens“ fungieren. Beim strukturierten, gestützten Üben können so Muster und Beziehungen leichter erkannt werden. Und überall da wo Worte fehlen, wo Kinder Schwierigkeiten haben, sich anderen mitzuteilen, können sie die Gedanken der Kinder, die entdeckten Strukturen und Muster sichtbar machen.
Der Einsatz von Darstellungsmitteln sollte nicht nur (aber natürlich auch!) als Hilfe für leistungsschwächere Kinder dienen, sondern ist für alle Kinder wichtig. Material ist als Darstellungsmittel sind mehr als nur Hilfsmittel zum Rechnen!
Ihr Einsatz im Unterricht wird leider oft als Zeichen von Lernschwäche interpretiert („Die Plättchen können dir helfen!“). Dies führt auch zuweilen zur Abwertung von erbrachten Leistungen („Du hast den Zahlenstrahl als Hilfe verwendet!“).
Das Material zielt insbesondere am Anfang, in der „Grundlegungsphase“, nicht sofort auf das (vor-) schnelle Auswendiglernen, sondern auf das einsichtige Entwickeln von Zahl- und Operationsvorstellungen. Erst im weiter fortgeschrittenen Lernprozess, in der „Automatisierungsphase“ rechnen die Kinder dann mit und abschließend auch ohne Anschauungsbezug schnell im Kopf mit dem Fokus auf das Auswendiglernen zum schnellen Abrufen der Kenntnisse (siehe auch Kopfrechnen).
Weiteres zu diesem Thema finden Sie auf der Seite „Operationsverständnis“.