Komplexe und realistische Fragestellungen mithilfe von Mathematik zu lösen – das bedeutet Modellieren.

Kinder erwerben dazu bereits vor Schuleintritt Kompetenzen.
Eine typische Situation kennt sicher jeder aus dem Familienleben: Das Tischdecken.
Es ist eine sehr komplexe Situation, die die Kinder praktisch bewältigen und bei der sie grundlegende Überlegungen anstellen, die das Modellieren charakterisieren.
Das Kind muss die Situation erfassen und notwendige Informationen erhalten oder erfragen. So ist zu klären, wie viele Personen am Tisch sitzen werden. Welches Geschirr wird gebraucht? Wie viele Teller, Tassen, Löffel, ...?
Auf der Grundlage der Informationen, seinem "Bild" (Modell) von der Situation "löst" das Kind das Problem handelnd und nimmt dabei u. a. Zuordnungen (Anzahl - Geschirrteile) vor und deckt den Tisch.
Es wird zum Abschluss prüfen, ob für alle der Tisch gedeckt ist.
Mit Eintritt in die Schule werden von Beginn an in der Auseinandersetzung mit Sachsituationen Modelle genutzt. Dazu gehören z. B.
-
das Verwenden von Quader, Würfel, Kugel, um die Umgebung abzubilden,
-
ein Vergleich der Wettervorhersage mit eigenen Messdaten,
-
das Prüfen gängiger Modelle zu Fahrpreisen des ÖPNV beim Planen eines Ausflugs,
-
das Betrachten von Blütenmodellen im Sachunterricht.
Für das Verständnis vom mathematischen Modellieren ist es bereits in dieser Phase nötig und sinnvoll mit den Kindern herauszustellen, dass das genutzte Modell einen bestimmten Zweck hat, nur einen Teil der Realität abbildet und Ergebnis eines "Nachdenkens" (Prozesses) ist (vgl. Henn 2000).
Die weitergehende Herausforderung besteht darin, mathematisches Modellieren als lebendige Auseinandersetzung mit Mathematik und damit als Form des Mathematiklernens bewusst im Unterricht zu nutzen.
Bis zum Ende der Grundschulzeit sollen Kinder in diesem Bereich folgende Kompetenzen erworben haben:
-
Sachtexten und anderen Darstellungen der Lebenswirklichkeit die relevanten Informationen entnehmen
-
Sachprobleme in die Sprache der Mathematik übersetzen, innermathematisch lösen und diese Lösungen auf die Ausgangssituation beziehen
-
Zu Termen, Gleichungen und bildlichen Darstellungen Sachaufgaben formulieren
(vgl. KMK 2004, S. 8)
Die Auswahl geeigneter Aufgaben wird durch die Ziele bestimmt, die bezüglich des Modellierens verfolgt werden. Da Modellieren ein komplexer (Bearbeitungs-)Prozess ist, kann es für das Verständnis hilfreich sein, auch Teilschritte reflektiert zu bearbeiten und zu üben. Geht es um eine Auswahl relevanter Informationen, sind über- und unterbestimmte Aufgaben gut geeignet (vgl. auch Maaß 2011). Kombinatorische Aufgaben können genutzt werden, um zu zeigen, dass Modellierungen von Sachsituationen unterschiedlich aussehen können.
Eigenaktivität
Lösen Sie die Aufgabe zunächst selbst.
Bei einer Geburtstagsfeier treffen sich sechs Kinder. Jedes gibt jedem die Hand.
Wie oft werden Hände geschüttelt?

Das Lösen dieser Aufgabe erfordert vielfältige Teilkompetenzen.
Dazu gehören zunächst...
|
das Erschließen und Verstehen der Sachsituation, um die für die Lösung relevanten Informationen zu entnehmen. |
Sechs Kinder geben sich die Hand. |
|
Sie sind die Grundlage dafür, die Sachsituation in eine vereinfachteDarstellung zu überführen. |
Es werden sechs Kinder der Klasse ausgewählt, die die Situation nachspielen sollen.
Für die Dokumentation kann jedes Kind z. B. durch einen Punkt veranschaulicht werden. |
|
Die Lösung kann zunächst handelnd ermittelt werden. |
Jedes der sechs Kinder gibt jedem die Hand und es wird gezählt, wie oft das geschieht. |
|
Das hilft das Sachproblem in die Sprache der Mathematik zu übersetzen (mathematisieren) und innermathematisch zu bearbeiten. |
Die Handlung kann durch die Kinder in verschiedener Form dargestellt werden.
-
Punkte für Kinder; das Händeschütteln wird durch Striche zwischen den Punkten gekennzeichnet; die Anzahl der Striche wird ermittelt
-
Verschriftlichung von Überlegungen: Das 1. Kind gibt fünf Kindern die Hand, das 2. Kind nur noch vier,... Die Gesamtzahl kann dann durch Addieren bestimmt werden (Verständnis der mathematischen Struktur)
|
|
Zum Bearbeitungsprozess gehört auch, dass die Kinder ihre Lösungen interpretieren und in der Sachsituation überprüfen (validieren). |
Dazu gehören Überlegungen wie:
-
Hat jedes Kind jedem die Hand geschüttelt?
-
Jedes Kind gibt fünf anderen Kindern die Hand und es sind sechs Kinder. Warum kommt nicht 5 · 6 = 30 heraus?
|
Schematisch kann man dieses Vorgehen wie folgt veranschaulichen
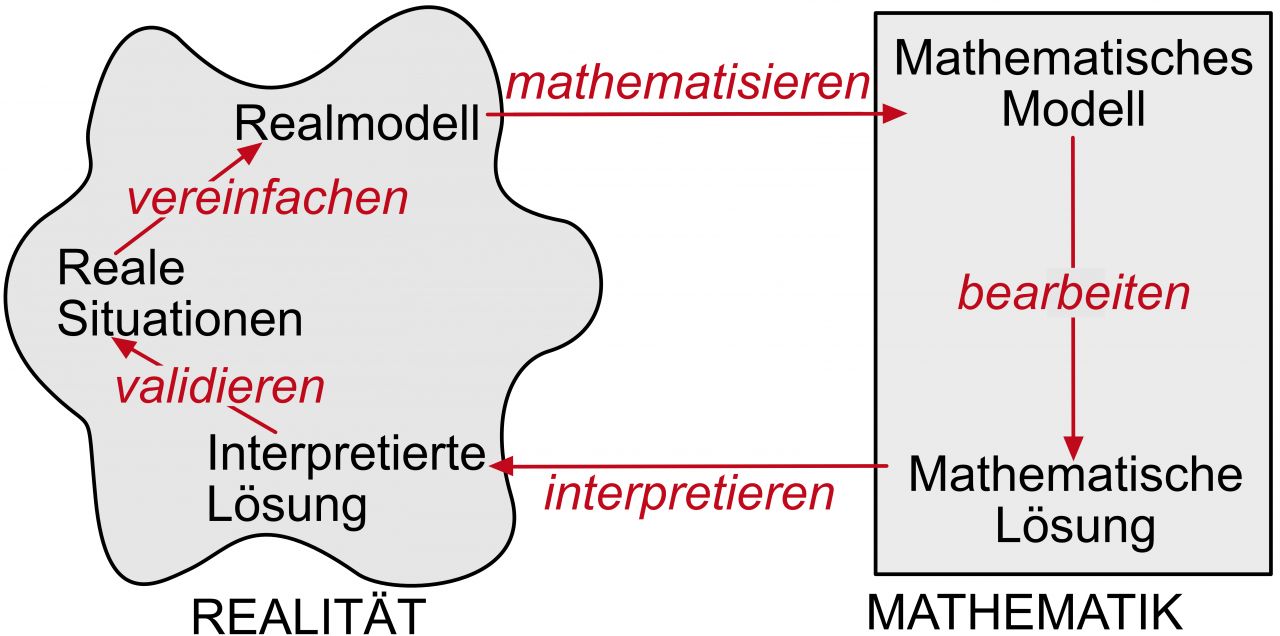 Modellierungskreislauf nach Maaß (2005b)
Modellierungskreislauf nach Maaß (2005b)
Als entscheidende Schnittstelle sind die Übersetzungsprozesse zu betrachten, die Modellieren im eigentlichen Sinne sind. Sie verbinden Umwelt und Mathematik. Im beschriebenen Beispiel wurden bildliche Darstellungen als Modell genutzt.
Die dritte Schülerlösung eröffnet bereits einen Zugang, um die mathematische Struktur des Problems zu erkennen. Die als Modell genutzten mathematischen Muster bzw. erkannten Strukturen können im Ergebnis von Lösungsprozessen auch in Form von Termen und Gleichungen ausgedrückt werden.
Um das Verständnis von Modellierungsprozessen zu fördern, sollten Kinder umgekehrt auch zu mathematische Modellen, wie bildlichen Darstellungen, Termen und Gleichungen (passende) Sachsituationen finden. Mehr dazu finden Sie im Partnerprojekt KIRA: Operationsverständnis Multiplikation.
Wie der Modellierungskreislauf zeigt, ist mathematisches Modellieren eine lebendige Auseinandersetzung mit Mathematik. Dabei werden bereits vorhandene Kompetenzen der Kinder sichtbar und der Erwerb von Kompetenzen ermöglicht. Folgende Schülertätigkeiten sollten gezielt beobachtet und qualitativ eingeschätzt werden.
Die Kinder
-
beschaffen sich gegebenenfalls zielgerichtet (weitere) Informationen mit Hilfe von verschiedensten Medien,
-
setzen (geeignete) heuristische Methoden zum Lösen von Problemen ein,
-
erkennen mathematische Zusammenhänge, beschreiben und begründen diese,
-
nutzen Fachbegriffe/-sprache, um Sachverhalte zu beschreiben, stellen Lösungsprozesse dar, kommentieren, reflektieren diese und überprüfen Lösungen,
-
schätzen die Vorgehensweisen von Mitschülerinnen und Mitschülern ein.
In diesen Beobachtungen ist erkennbar, dass der Kompetenzerwerb aller prozessbezogenen, mathematischen Kompetenzen eng vernetzt ist und die erworbenen Kompetenzen über die Mathematik hinaus von fachübergreifender Bedeutung sind.
Als klassische Modellierungsaufgaben werden auch FERMI-Aufgaben angesehen. Dazu finden Sie weitere Ausführungen und ein Unterrichtsbeispiel auf Seiten des PartnerprojektsKIRA: Fermi-Aufgaben.
Vielleicht bewegten Sie inzwischen folgende Fragen: In welcher Beziehung steht das mathematische Modellieren zum traditionelle Sachrechnen? Geht es um mehr und/oder um etwas grundsätzlich anderes?
Dazu finden Sie weitere Ausführungen unter Sachrechnen.