Kopfrechnen im Kontext von gutem Mathematikunterricht
Um sich diesen Fragen zu nähern, betrachten wir zunächst, welche Bedeutung die Bildungsstandards dem Kopfrechnen zuschreiben. Anschließend soll beschrieben werden, wie in einem auf ein verständiges Mathematiktreiben ausgerichteten Unterricht das Kopfrechnen sinnvoll eingebunden werden kann.
Verankerung in den Bildungsstandards
Traditionell wurde unter Kopfrechnen z. B. das Aufsagen der Einmaleins-Aufgaben verstanden, man verbindet damit Formate wie "Eckenrechnen" und das unsystematische Abfragen von Aufgaben. Dabei spielten Zusammenhänge zwischen den Aufgaben keine Rolle, was wie in dem Beispiel im
Einstieg dazu führt, dass auch die Kinder diese nicht herstellen und jede Aufgabe isoliert betrachten.
In den Bildungsstandards im Bereich "Zahlen und Operationen" findet sich folgende Kompetenzanforderung:
Die Kinder sollen am Ende der vierten Jahrgangsstufe „die Grundaufgaben des Kopfrechnens (Einspluseins, Einmaleins, Zahlzerlegungen) gedächtnismäßig beherrschen, deren Umkehrungen sicher ableiten und diese Grundkenntnisse auf analoge Aufgaben in größeren Zahlenräumen übertragen [und] mündliche und halbschriftliche Rechenstrategien verstehen und bei geeigneten Aufgaben anwenden" (KMK 2005, S. 9).
Allgemein kann man unter Kopfrechnen alles Rechnen verstehen, das ohne die Notation von Zwischenschritten auskommt und daher im Kopf stattfindet (vgl. Krauthausen & Scherer 2007). Abgegrenzt davon werden das
halbschriftliche und
schriftliche Rechnen.
Ziel eines zeitgemäßen Mathematikunterrichts ist es unter anderem, ein Gefühl für Zahlen und den Umgang mit ihnen zu bekommen und flexibles Rechnen zu ermöglichen. Um das zu erreichen, ist Kopfrechnen von zentraler Bedeutung.
Kopfrechnen ist also wichtig, um
-
flexibles Rechnen zu ermöglichen,
-
das Arbeitsgedächtnis zu entlasten,
-
in größeren Zahlenräumen geschickt rechnen zu können,
-
die Plausibilität von Ergebnissen abschätzen zu können,
-
einen Zahlen- und Aufgabenblick zu entwickeln.
Dazu sind automatisierte Wissensbestandteile erforderlich, aber „das Lernen des Kleinen Einspluseins und Einmaleins erfolgt auf der Grundlage von Beziehungen, die die Aufgaben miteinander verbinden. Das Bewusstmachen solcher Beziehungen reduziert den Anteil der einzuprägenden Aufgaben und führt zu Assoziationen, die das Lernen stützen" (Rasch & Schütte 2012, S. 69-70).
Wie sollte also das Kopfrechnen in einen zeitgemäßen Mathematikunterricht eingebunden werden?
Grundlagen für das Kopfrechnen
Es reicht also nicht, die Aufgaben einfach nur auswendig zu lernen. „Beziehungsreiches und automatisierendes Üben gehört zu einem erfolgreichen Lernen des kleinen Einspluseins genauso dazu wie die gründliche Erschließung von Rechenstrategien. Beides muss Hand in Hand und parallel verlaufen" (Padberg & Benz 2011, S. 101; vgl. auch die Seite
Üben).
Eigenaktivität
Rechnen Sie die folgenden Aufgaben im Kopf aus.
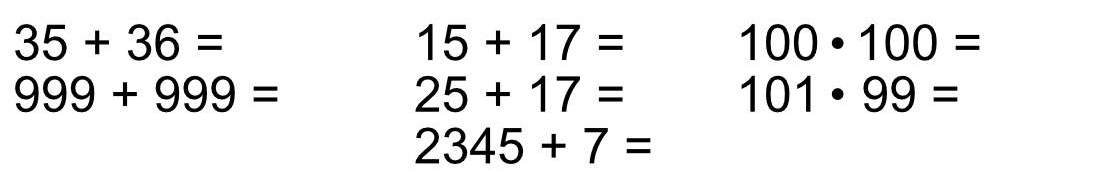
Reflektieren Sie, wie Sie vorgegangen sind.
Was ist für schnelles Kopfrechnen notwendig?
-
Zahlenblick bzw. Aufgabenblick:
Um zu erkennen, wie man eine Aufgabe möglichst geschickt ausrechnen kann, müssen Kinder ein Gefühl dafür bekommen, wie eine Zahl "aussieht", welche Zusammenhänge sich ergeben, wie eine Aufgabe zerlegt werden kann (vgl.
Zahlvorstellung erwerben,
Operationsverständnis aufbauen).
-
Strategien zum geschickten Rechnen:
Um sich Ergebnisse erschließen zu können, müssen Kinder Ableitungsstrategien kennen, sichere Operationsvorstellungen haben und Rechengesetze flexibel einsetzen können.
-
Auswendig gewusste Aufgaben:
Die sind notwendig (aber eben ganz bestimmte), um Analogien und Zusammenhänge nutzen zu können. Außerdem sollten die Aufgaben nicht isoliert, sondern im Zusammenhang gelernt werden, um diese Zusammenhänge als Gedächtnisentlastung nutzen zu können.
Wege zum sicheren Kopfrechnen
Im Folgenden wird allgemein beschrieben, welche Aspekte bei der Entwicklung einer sicheren Kopfrechenkompetenz eine Rolle spielen. Im
Unterricht werden diese allgemeinen Aspekte dann an einem Beispiel konkretisiert.
Folgende Phasen sind dabei von Bedeutung:
-
Verstehensorientierte Einführung von Aufgaben, sicherer Aufbau von Grundvorstellungen durch materialgestützten Vorstellungsaufbau (siehe Zahlvorstellung erwerben, Operationsverständnis aufbauen)
-
Produktives Üben, um Zusammenhänge und Strukturen zu verstehen und nutzen zu lernen (siehe Üben)
-
Automatisieren (von ganz bestimmten Aufgaben und als Grundlage, um Ergebnisse herzuleiten - das wird ebenfalls geübt)
-
Flexibles Rechnen, weitere entdeckende Lernprozesse im größeren Zahlenraum (siehe. Spiralprinzip)
Dies ist nicht als Einbahnstraße zu verstehen. Es wird zwischen den Phasen gewechselt; sie werden auf vielfältige Art und Weise miteinander verknüpft. Wichtig ist: Die Automatisierung bezieht sich nicht nur auf das Auswendiglernen und steht erst am Ende des Lernprozesses.
Eine gute Übersicht bietet der folgende Film, der diese Prozesse im Unterricht darstellt:
In diesem Film ist der gesamte Prozess im Überblick dargestellt. Es wird deutlich, dass die verschiedenen Phasen an vielen Stellen ineinandergreifen und dass die Kinder sich zu einem bestimmten Zeitpunkt an unterschiedlichen Stellen dieses Prozesses befinden.
Auf der Unterseite "Unterricht" wird noch einmal dargestellt, wie man bei der anschaulichen Einführung der Aufgaben vorgehen kann.
Was müssen die Kinder lernen?
Für die Frage, welche Aufgaben automatisiert werden sollten, stellt der Blitzrechenkurs (ursprünglich Wittmann/ Müller 1990/1992) eine „ausgearbeitete Konzeption für die Kopfrechenpraxis" (Krauthausen & Scherer 2007, S. 46) dar. Für alle vier Grundschuljahre werden mit den aufeinander aufbauenden Blitzrechenübungen die wichtigen Grundbausteine zur Entwicklung eines Zahlen- und Aufgabenblicks gelernt, wobei der Weg von der verstehensorientierten Einführung bis zum Auswendigwissen dargestellt wird.
Im
Material finden Sie mit den Blitzrechenplakaten eine Übersicht über den Blitzrechenkurs.
Hier zeigt sich auch, dass die zu automatisierenden Aufgaben in den verschiedenen Zahlenräumen sich wiederholen, strukturell zusammenhängen und aufeinander aufbauen:
-
Zerlegungen der 10 → Ergänzen zum nächsten Zehner → Ergänzen zum Hunderter → Ergänzen bis 1000 → Ergänzen bis 1 Million
-
Verdoppeln/Halbieren im Zwanzigerraum → im Hunderterraum → im Tausenderraum → im Millionraum
-
Zahlenreihe → Zählen in Schritten
-
Übungen zum "Blitzsehen" (Wie viele?) in allen Zahlenräumen
-
usw.
Begleitend dazu müssen im Unterricht Strategien thematisiert und geübt werden. Dabei spielen Erfahrungen mit Analogien, Ableitungen und dem Verändern von Aufgaben eine wesentliche Rolle.
Folgende Strategien müssen also schon im ersten Schuljahr im Zwanzigerraum thematisiert werden:
-
Tauschaufgaben (3 + 8 = 8 + 3)
-
Analogieaufgaben (1 + 2 / 11 + 2 / 111 + 2)
-
Nutzen von Nachbaraufgaben (10 + 8 / 9 + 8)
-
Schrittweises Rechnen (6 + 8 = 6 + 4 + 4)
-
Gegensinniges Verändern (6 + 8 = (6 + 1) + (8 - 1) = 7 + 7 = 14)
Auf der Unterseite "Unterricht" wird exemplarisch an den Verdopplungsaufgaben und ihren Ableitungen gezeigt, wie man vorgehen kann.