Kopfrechnen im Zwanzigerraum am Beispiel der Verdopplungsaufgaben und ihrer Ableitungen
Die Aufgaben des Kleinen Einspluseins sind neben dem Einmaleins eine der wichtigsten Grundlagen der Grundschulmathematik, die sicher beherrscht werden sollten, um dann in größeren Zahlenräumen flexibel rechnen zu können.
Im Folgenden soll exemplarisch anhand der Verdopplungsaufgaben im Zwanzigerraum gezeigt werden, wie man auf dem Weg zum schnellen Kopfrechnen vorgehen kann:
Voraussetzungen bei den Kindern
Vor der im Folgenden beschriebenen Unterrichtseinheit sollten nachstehende Aspekte im Unterricht bereits angesprochen worden sein:
-
Das Zwanzigerfeld und seine Strukturen sollten bekannt sein, weil es hier als zentrales Darstellungsmittel dient.
-
Das Blitzsehen am Zwanzigerfeld, damit die Strukturen der Verdopplungsaufgaben "gesehen" werden können.
-
Das Teile-Ganzes-Verständnis im Zwanzigerraum, damit die unterschiedlichen Aufteilungen der Mengen verstanden und genutzt werden können.
-
Das Vertrautsein mit Gesprächen über Strukturen: "Wie hast du das so schnell gesehen?", damit die Zusammenhänge und die geschickten Sehweisen bewusst gemacht werden können.
-
Das Wissen, was "Verdoppeln" (z. B. Verdoppeln mit dem Spiegel) heißt, um die Grundlage der Operation zu verstehen.
Anschauliche Einführung der Verdopplungsaufgaben
Als erster Schritt ist die anschauliche, materialgestützte Einführung von Bedeutung. Dabei wird das Material (hier: Zwanzigerfeld und Wendeplättchen) sowohl von der Lehrkraft als auch von den Kindern genutzt, um Verdopplungsaufgaben auf dem Zwanzigerfeld strukturiert zu legen:
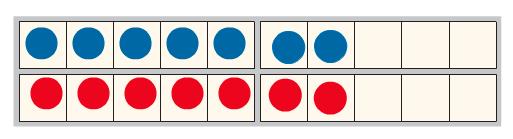
Anhand des Bildes werden Strategien besprochen, wie man das Ergebnis schnell sehen kann. Dabei werden auch die Strukturen der Ausgangszahl nochmal thematisiert (Kraft der 5):
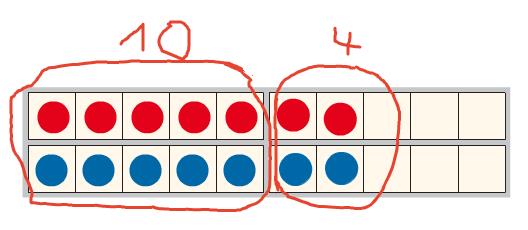 7 + 7 = 10 + 4
7 + 7 = 10 + 4
Knackpunkt:
Wichtig ist es dabei, die konkrete Handlung nicht zu vernachlässigen, lange mit der Anschauung zu arbeiten und die Strukturen immer wieder zu versprachlichen und dadurch bewusst zu machen.
"Ich lege sieben Plättchen ins Zwanzigerfeld. Das ist ein Fünfer und zwei einzelne Plättchen. Wenn ich das verdopple, habe ich das Gleiche unten noch einmal. Die zwei Fünfer sind 10, daneben liegen noch zwei mal zwei, also vier. Das Ergebnis ist 14!"
Es geht darum, den Kindern ein "Bild im Kopf" zu ermöglichen. Dazu kann man sich nach Wartha und Schulz (2014, S. 64) am Vier-Phasen-Modell orientieren, das die systematische Ablösung vom konkreten Material beschreibt.
Erst wenn eine sichere Vorstellung da ist, sollten die Verdopplungen auswendig gelernt werden, z. B. mit Hilfe einer Übungskartei (PIK AS o. J.). Siehe unter PIKAS: Unterrichtsmodul: Zahlen und Operationen – Addition üben.
Ableitungsstrategien kennenlernen
Auch der zweite Schritt erfolgt materialgestützt: Die Verdopplungsaufgaben werden zur Ableitung weiterer Aufgaben genutzt. Dazu werden die Aufgaben am Zwanzigerfeld verändert. Wieder ist das Ziel ein Vorstellungsaufbau bei den Kindern: Wie ändert sich das Bild und was bedeutet das für meine Zahlen? Wichtig ist es, dass dies nicht nur an bildlichen Darstellungen im Buch nachvollzogen wird, sondern dass die Handlungen konkret durchgeführt und sprachlich begleitet werden und zwar nicht nur von der Lehrkraft als Demonstration, sondern auch von den Kindern selbst.
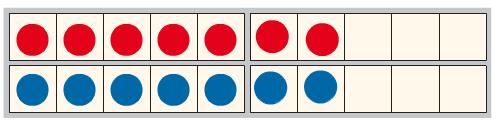 7 + 7 = 14
7 + 7 = 14
"Was passiert, wenn ich ein blaues Plättchen weglege? Wie verändert sich die Aufgabe? Was bedeutet das für mein Ergebnis?"
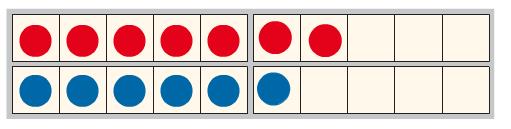 7 + 6 =
7 + 6 =
"Was verändert sich, wenn ich ein (rotes) Plättchen dazulege?"
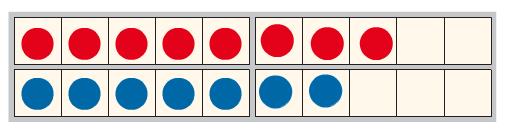 8 + 7 =
8 + 7 =
Diese konkreten Handlungen werden dann auf die symbolische Ebene übertragen und auch dort wieder sprachlich begleitet (z. B. durch einen Wortspeicher, siehe Sprachförderung). Mit Hilfe von Kärtchen, auf denen Terme und Satzbausteine stehen, können verschiedene Aufgaben einander zugeordnet und operative Veränderungen verdeutlicht werden. Auch in dieser Phase kann ein Rückgriff auf die konkrete Darstellung am Material an vielen Stellen und für viele Kinder immer wieder eine hilfreiche Unterstützung sein.
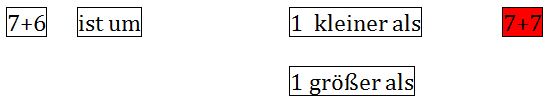
Durch die Verdeutlichung von Aufgabenbeziehungen soll vermieden werden, dass die Kinder, wie der Junge in unserem Einstiegsbeispiel, die Aufgaben als von einander isoliert wahrnehmen.
Weitere Übungen im Unterricht
Durch produktive Übungen können diese Aufgabenbeziehungen dann gefestigt werden. Dazu bieten sich z. B. Sortieraufgaben an, bei denen wieder die Aufgabenkarten von PIKAS: Unterrichtsmodul: Zahlen und Operationen – Addition üben genutzt werden:
 Bildunterschrift
Bildunterschrift
Es bieten sich vielfältige Sortieraufgaben an, z. B. Welche Aufgaben passen zusammen? Was verändert sich? Was bleibt gleich? Bei welchen Aufgaben kommt das Gleiche heraus? Warum?
Welche sind leicht, welche sind schwer?
Analog wird mit anderen zu automatisierenden Aufgaben, z. B. den Zerlegungen der 10, gearbeitet (vgl. Aufgabenkärtchen von Material). Dabei wird die Menge der auswendig zu lernenden Aufgaben reduziert und es werden die Zusammenhänge zwischen Aufgaben genutzt.
Eine übersichtliche Darstellung der Aufgabenbeziehungen im Zwanzigerraum stellen die verschiedenen Einspluseins-Tafeln dar, die die Kinder am Ende des ersten Schuljahres kennenlernen (vgl. z. B. Zahlenbuch 1, Fredo und Co 1). Auch zu diesen lassen sich vielfältige Sortier- und Legeaufgaben finden, die immer wieder die Aufgabenbeziehungen in den Blick nehmen.
Im weiteren Unterricht sollte die Frage, wie sich eine Aufgabe geschickt und mit möglichst wenig Aufwand ausrechnen lässt, immer wieder eine Rolle spielen (Aufgabenblick, flexibles Rechnen, vgl. auch
Halbschriftliche Rechnenstrategien).