Zahlen haben in der Lebenswelt unterschiedliche Funktionen und Bedeutungen. Die damit verbundenen vielfältigen Zahlvorstellungen müssen Kinder aufbauen, um rechnen zu lernen. Neben der Einsicht in die Zahlaspekte und den Erwerb von Zählstrategien sind dafür das Entdecken und die Nutzung von Zusammenhängen und von Beziehungen zwischen Zahlen zentral. Den Darstellungen von Zahlen und ihren verschiedenen Darstellungsformen kommt ebenfalls eine bedeutende Rolle zu (Selter/Zannetin 2018).
In Anlehnung an diese Fragen aus dem Einstieg sollen auf dieser Seite die folgenden Bausteine zur Entwicklung von Zahlvorstellungen erläutert werden
Zahlen sind abstrakt und bekommen erst dann eine Bedeutung, wenn wir Vorstellungen dazu entwickeln. Je nachdem in welchem Kontext Zahlen genutzt oder dargestellt werden, können sie verschiedene Bedeutungen haben und Unterschiedliches ausdrücken bzw. kann Unterschiedliches mit ihnen ausgedrückt werden.
Man unterscheidet dabei die folgenden "Grundvorstellungen", die auch "Zahlaspekte" genannt werden:
 (Selter/Zannetin 2018, S. 30)
(Selter/Zannetin 2018, S. 30)
Kinder sollen dabei nicht explizit zwischen diesen Vorstellungen unterscheiden können, aber die Zahlen in den verschiedenen Kontexten deuten lernen.
Die Zahlaspekte sind auch bedeutsam, wenn es darum geht, Zählkompetenzen zu erwerben. Zwar können schon viele Kinder vor Schuleintritt "zählen", aber um durch Zählen die Anzahl einer Menge von Objekten zu bestimmen oder auch als erste Lösungsstrategie von Rechenaufgaben reicht es nicht, dass die Kinder die Zahlwortreihe wie ein "Gedicht aufsagen" können.
Eigenaktivität
Stellen Sie sich vor, die Buchstaben des des Alphabets sind Zahlworte (a = 1, b = 2, ... v = 22).
Achtung: Übersetzen Sie bei den Aufgaben die Buchstaben nicht zurück in Zahlen. Diese Hilfe steht Kindern nicht zur verfügung (vgl. Wartha & Schulz 2013, S. 43).
Zählen Sie bitte vorwärts ab a.
Zählen Sie bitte vorwärts ab n.
Zählen Sie bitte rückwärts ab k.
Nennen Sie den Vorgänger von q.
Zeigen Sie auf einmal h Finger.
Reichen beide Hände, um l Finger zu zeigen?
Berechnen Sie h minus e.
Was ist Ihnen leichter gefallen? Bei welchen Aufgaben hatten Sie Schwierigkeiten?
Deutlich wird also, dass die Zählkompetenz zwei wesentliche Aspekte umfasst, die von zentraler Bedeutung sind. Zum einen das sichere Beherrschen der Zahlwortreihe und zum anderen das Sichere Abzählen von Mengen (Hasemann & Gasteiger, 2014, S. 17).

In den Zählprozessen (zur Anzahlbestimmung als auch beim Zählen als Strategie beim Lösen von Aufgaben) spielen die folgenden Zählprinzipien eine zentrale Rolle, die die Kinder verinnerlichen müssen:
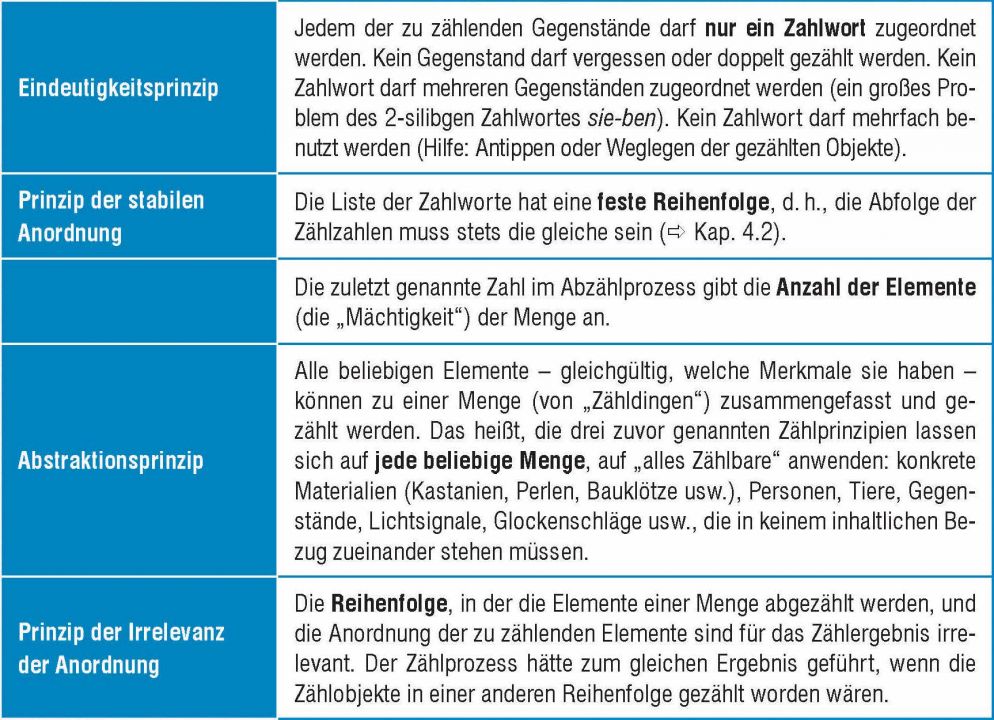 (Götze/Selter/Zannetin 2019, S. 27)
(Götze/Selter/Zannetin 2019, S. 27)
Deutlich wurde bereits im Einstieg, dass Vorstellungen von Zahlen unter anderem in der Auseinandersetzung mit unterschiedlichen Darstellungen, durch die sie verkörpert werden, entstehen. Die Kinder müssen daher lernen, sowohl Darstellungen von Zahlen zu deuten als auch selbst Zahlen darzustellen.
Wir unterscheiden folgende Darstellungsformen: durch Handlung mit Material, durch ein Bild, durch gesprochene oder geschriebene Sprache sowie Darstellungen (Mathesprache).
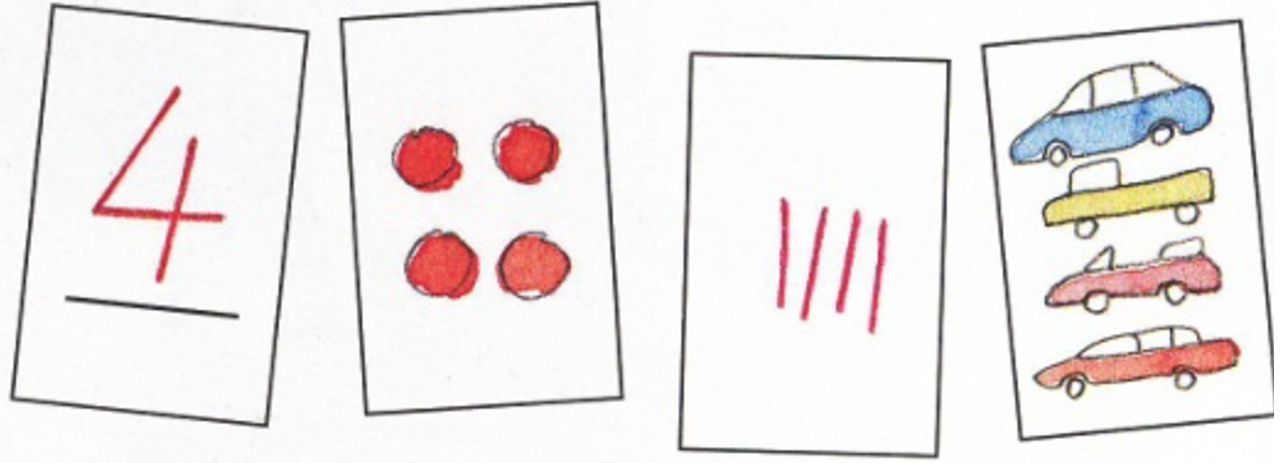
Auch hier sind die Zahlaspekte von Bedeutung. Die ordinale Deutung von Zahlen als Position in einer Reihe kann entsprechend mithilfe von linearen Repräsentationen dargestellt werden können (wie Hunderterkette oder Zahlenstrahl). Werden Zahlen kardinal, also als Anzahlen erfasst, werden sie dafür anfänglich in gruppenweisen, später häufig in flächigen Darstellungen repräsentiert (wie Punktefelder oder Rechtecksdarstellungen).
Sollen Zahlen als Anzahlen mit Plättchen dargestellt werden, kann dies dabei sowohl durch strukturierte oder durch unstrukturierte Mengenbilder erfolgen.
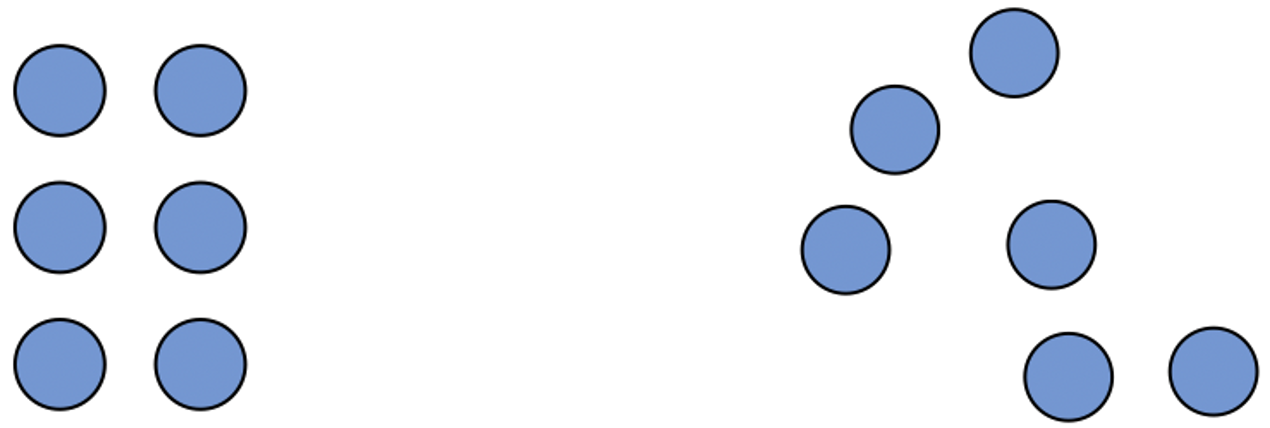
Dabei wird die Kompetenz, Anzahlen von bis zu 4 Objekten auf einen Blick - also nicht zählend - zu erfassen, als simultane Zahlerfassung bezeichnet. Diese Fähigkeit erwerben viele Kinder häufig bereits im Vorschulalter (Padberg/Benz 2011, S. 17).
Damit die Lernenden langfristig die Anzahlen von Objekten nicht durch einzelnes Auszählen ermitteln, sondern die Strukturen der Darstellungsmittel nutzen, müssen sie Fähigkeiten in der quasi-simultanen Zahlauffassung besitzen, das bedeutet, dass sie die Menge in kleinen Teilmengen strukturieren, um so die Gesamtzahl zu ermitteln.
 (Aus Götze/Selter/Zannetin 2019)
(Aus Götze/Selter/Zannetin 2019)
Im Verlauf der Grundschulzeit sollen die Kinder dann lernen, andere Stützpunkt-Anzahlen wie 5, 10, 20 oder 100 in strukturierten Darstellungen wie Zwanziger-, Hunderter- oder Tausenderfeldern auf einen Blick zu erkennen.
Das schnelle Erfassen von Zahlen, die mit Material oder bildlich dargestellt werden, wird also vor allem durch das Nutzen von Strukturen ermöglicht. Allgemein sind Fähigkeiten zum Erkennen und Nutzen von Beziehungen zwischen Zahlen eine wichtige Voraussetzung für ein tragfähiges und flexibles Zahlverständnis.
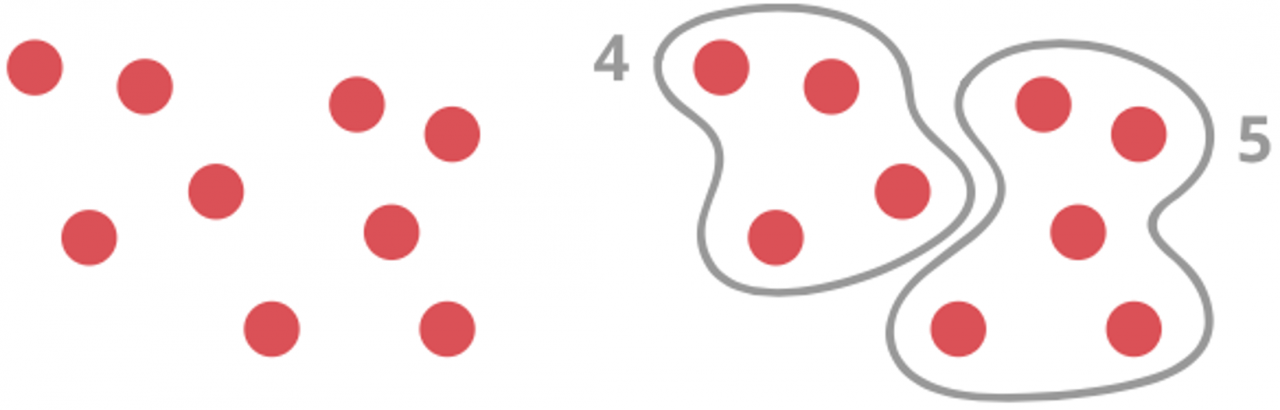
Wie im Beispiel oben auch im Anfangsbeispiel von Nele können Zahlen bzw. Anzahlen unterschiedlich zerlegt werden. In diesem Kontext spielen die Teil-Ganzes-Zahlbeziehungen eine wichtige Rolle (Gaidoschik 2010; Gerster/Schultz 2004, S. 78ff.). Das dahinterliegende Teile-Ganzes Konzept besagt, dass sich eine Menge (und somit jede Zahl) in kleinere Teilmengen (hier 4 und 5) zerlegen bzw. solche Teilmengen auch wieder zu einem Ganzen (9) zusammensetzen lassen. Die Entwicklung der Fähigkeit zur Betrachtung von Zahlen in Teil-Teil-Ganzes-Beziehungen gilt als zentrale Herausforderung eines verständnisorientierten Mathematikunterrichts (vgl. Resnick 1983). Im Verlauf der Grundschulzeit kommt dann dem stellengerechten Zerlegen von Zahlen eine zentrale Bedeutung zu (beispielsweise lässt sich 125 in 1 Hunderter, 2 Zehner und 5 Einer zerlegen), da dies Vorraussetzung für die Ausbildung des Stellenwertbverständnisses ist (siehe Modul "Stellenwertverständnis").
Des Weiteren sollen die Kinder lernen, Anzahlen zu vergleichen und dabei feststellen, dass z.B. in einer Menge mehr Objekte sind als in der anderen Menge (mehr/ weniger; gleich viel). Auch am Zahlenstrahl können Zahlen in Bezug zu anderen Zahlen positioniert und interpretiert werden (ist größer/ kleiner; ist der Vorgänger/ Nachfolger).
Die Ausbildung, Erweiterung und Festigung dieser Fähigkeiten ermöglicht es, dass die Kinder ein umfassendes Zahlverständnis erwerben. Wie und mit welchen Übungen das gelingen kann, soll auf der Seite "Unterricht" beispielhaft erläutert werden.