Unterricht
Deutlich wurde, dass zum Ausbau umfassender Zahlvorstellungen viele Teilfähigkeiten entwickelt werden müssen. Im Anfangsunterricht sollte dafür zunächst an die Vorstellungen der Kinder angeknüpft und die unterschiedlichen Fähigkeiten durch geeignete Übungen erweitert werden (mehr dazu finden sie auf unserer Partnerprojektseite "Mahiko"; Verweise siehe unten).
Anknüpfend an das Beispiel aus dem Einstieg wollen wir auf dieser Seite das eher übergreifende Format "Zahlen unter der Lupe" näher erläutern
- Einführung und Durchführungshinweise
- Differenzierungsmöglichkeiten
- Reflexion und Weiterarbeit
Einführung und Durchfürhungshinweise
Die Lehrperson erklärt den Kindern, dass sie nun in die Rolle eines Zahlendetektives schlüpfen und einzelne Zahlen genau untersuchen werden. Ziel ist es, dass die Kinder umfassende Zahlvorstellungen (Darstellen von Zahlen, flexibles Wechseln zwischen unterschiedlichen Zahldarstellungen, Entdecken von Beziehungen zwischen Zahlen etc.) entwickeln und erweitern.
Wie die Zahlen untersucht werden, zeigt die Lehrkraft zum Beispiel anhand der Zahl 5. Dazu präsentiert die Lehrperson den Kindern das Arbeitsblatt "Zahlen unter der Lupe ZR 10/20" z.B. als Folie auf dem OHP und notiert dann die zu untersuchende Zahl (z.B. die 5/10) in allen Lupen (vgl. https://pikas.dzlm.de/node/685).
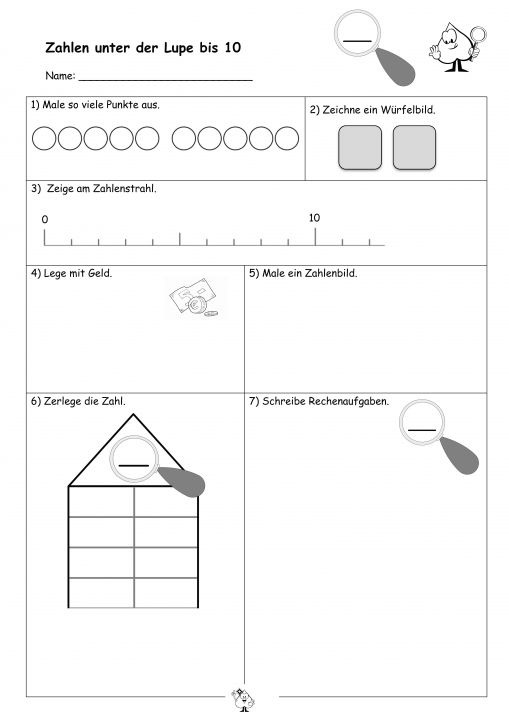
Aufgabe ist es, dass die Kinder für die jeweilige Zahl ...
- die entsprechende Anzahl an Punkten auszumalen
- das entsprechende Würfelbild zu malen und die Zahl in eine Stellenwerttafel einzutragen
- die Zahl am Zahlenstrahl einzuordnen (auf dem Zahlenstrahl von 0-20 ist für jede Zahl ein Strich vorgesehen, so dass sich die "gesuchte Zahl" genau zuordnen lässt.)
- die Zahl als Geldbetrag zu legen (mit Scheinen oder Münzen)
- die Zahl als Zahlenbild (bspw. als Fingerbild) darzustellen
- die Zahl mit dem Zerlegungshaus (zunehmend systematisch) zu zerlegen und möglichst alle Zerlegungen zu finden (durch das nach unten offene Zerlegungshaus soll die Anzahl nicht vorgegeben werden, den Kindern sollte aber bewusst sein, dass sie es weiterzeichnen können)
- weitere eigene Ideen zu Aufgaben mit der Zahl zu notieren (die Zahl kann in der Aufgaben vorkommen z.B. als Summand oder Ergebnis)
Wichtig ist, dass die Kinder (ggf. die Lehrperson) erklären, warum die Felder wie ausgefüllt werden. Hier bietet es sich an, gemeinsame Sprechweisen zu finden, die im besten Fall von den Kindern selbst kommen.
In der Arbeitsphase bearbeiten die Kinder dann selbstständig zunächst ein Arbeitsblatt "Zahlen unter der Lupe ZR 10" zu einer vorgegebenen Zahl und können dann mit einer selbstgewählten Zahl fortfahren.
Die Kinder sollten die Möglichkeit haben, Darstellungsmittel z.B. als Forschermittel nutzen zu können. Für die Arbeitsphase benötigen Sie also die Arbeitsblätter (blanko), Spielwürfel, Spielgeld, 10er/ 20erFelder und Plättchen.
Differenzierungsmöglichkeiten
Aufgrund der Heterogenität der Lerngruppen werden nicht alle Kinder von Anfang an (Klasse 1) "Zahlen unter der Lupe" vollständig bearbeiten können.
Bei Schwierigkeiten können die folgenen Impulsen zum Anfertigen der einzelnen Darstellungen hilfreich sein:
- "Male so viele Punkte an, wie die Zahl in der Lupe es anzeigt."
- "Wie kannst du die Zahl in der Lupe würfeln? Male die Würfelaugen auf."
- "Die Striche stehen für die Zahlen von null bis zwölf. Wo ist die Zahl aus der Lupe? Schreibe die Zahl über den richtigen Strich."
-
"Lege die Zahl in der Lupe mit Spiegelgeld als Euros. Wie könnte das aussehen? Gibt es noch mehr Möglichkeiten? Du könntest sie auch auf der Rückseite aufzeichnen."
(Tipp: Es bietet sich an, hier über verschiedene Möglichkeiten zu sprechen, wie der Geldbetrag dargestellt werden kann. Die Euromünzen und -scheine sollten den Kindern bekannt sein.) -
"Stelle die Zahl in der Lupe als Bild dar."
(Hinweis: Die Ideen und Darstellungsmöglichkeiten der Kinder aufgreifen. Folgende Darstellungen können eingeführt werden: Fingerbilder; ein- oder zweizeilig lineare Produktdarstellung (z.B. Punktereihe oder 10er/20erFeld; Zehnerstangen/Einerwürfel; Würfel (andere Mgl. als bei 2); Gegenstände /z.B. Blumen oder Bälle)) -
"Schreibe alle Zerlegungen der Zahl in der Lupe, die du findest auf. Du kannst das Haus auch noch verlängern."
(Hinweis: Das Zerlegungs- bzw. Zahlenhaus und seine Eintragungen sollten den Kindern durch verschiedene Unterrichtsaktivitäten bekannt sein (z.B. u.a. durch Schüttelboxen) -
"Schreibe Aufgaben, in der die Zahl aus der Lupe vorkommt." "Kennst du mehrere verschiedene Aufgaben?"
Hier ist es wichtig, dass den Kindern in der Einführung gezeigt wird, dass die erforschte Zahl irgendwo in der Aufgabe vorkommen darf (als Ergebnis, Minuend, Summand...)
Um wirklich allen Kindern eine erfolgreiche Arbeitsphase zu ermöglichen, kann es sinnvoll sein, zusätzlich eine Tipp-Karte in Form eines ausgefüllten Arbeitsblatts "Zahlen unter der Lupe" ZR 20 z.B. wie im Folgenden zur Zahl 5 bereitzustellen.

Es ist aber auch möglich, dass Kinder bereits auch in einem, größeren Zahlenraum Zahlen untersuchen möchten und können. Das Potential des Formats liegt darin, dass es auf größere Zahlenräume erweiterbar ist und dabei neben weiteren Darstellungsmöglichkeiten (Stellentafel) auch auf weitere Zahlbeziehungen eingegangen werden sollte (Zehner/Hunderterergänzung; Verdoppeln und Halbieren)
Reflexion und Weiterarbeit
In einer gemeinsamen Schlussphase können einzelne Aufgaben besprochen und verglichen werden. Besonders interessanten Gesprächsanlass bieten die Aufgaben 5-7 (ZR 10) bzw. 8-11 (ZR 20).
Mögliche Reflexionsimpulse könnten sein:
- Welche und wie viele Möglichkeiten gibt es, die Zahl als Geldbetrag zu legen? (Aufgabe 4)
- Bei welchem Bild ist die Anzahl sehr schnell zu erkennen? Warum? Wie ist die Strukturierung? (Augabe 5)
- Welche und wie viele Zerlegungen sind möglich? Wie können sie systematisch notiert werden? (Aufgabe 6)
Auch können sich einzelne Kinder in Kleingruppen bzw. zur Mathekonferenz treffen, um Ergebnisse miteinander zu vergleichen (zu einer gemeinsamen Zahl) oder eine vorgegebene Fragestellung zu reflektieren (vielleicht auch zu unterschiedlichen Zahlen).
Die Arbeitsblätter "Zahlen unter der Lupe" (ZR 10, ZR 20, ZR 100, ZR 1000 und ZR frei) sollten im Mathe-Regal offen zugänglich sein. So kann dieses Format immer wieder von den Kindern auch in der freien Arbeitszeit bearbeitet werden oder in einen (individuellen) Wochenplan integriert werden, so dass sowohl das Kind als auch die Lehrperson die Arbeit mit diesem Format ganz individuell nach Bedarf steuern können.
Im Bereich Material finden Sie weiterführende Links zum Erkennen, Darstellen, Zerlegen und Vergleichen von Zahlen.

