Wie kann Operationsverständnis aufgebaut werden?
Einen wichtigen Aspekt bei der Behandlung der Rechenoperationen (und damit beim Aufbau des Operationsverständnisses) stellen Darstellungswechsel dar (vgl. Akinwunmi & Deutscher 2014; PIK AS 2012). Nachfolgend wird
eine mögliche Unterrichtsaktivität zur Förderung des Darstellungswechsels bei der Subtraktion aufgeführt. Weitere mögliche Unterrichtsaktivitäten (auch zu anderen Rechenoperationen) finden Sie im
Materialteil.
Im Folgenden wird das Spiel "Minustrio" anhand dieser Punkte aufgezeigt:
Das Spiel Minustrio besteht aus mehreren "Trio"-Spielkarten, also immer drei Karten, die zusammengehören: eine Rechenaufgabe, ein dazu passendes Zwanzigerfeld und ein selbstgemaltes Bild.
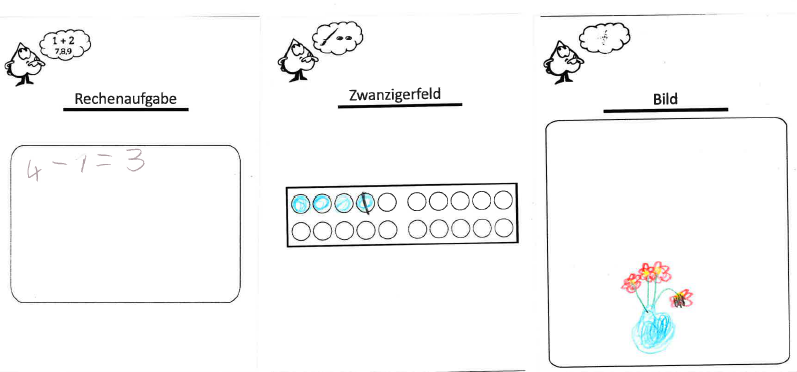
Das Herstellen des Spiels Minustrio dient im Mathematikunterricht der Primarstufe in mehrerer Hinsicht:
-
als Motivation für die Kinder
-
zur Wiederholung und Vertiefung der Subtraktion der 1. und Anfang der 2. Klasse
-
zur Förderung des Darstellungswechsels zwischen Bild und Mathesprache (auber auch Sprache)
Die Kinder sollten bereits als Lernvoraussetzung die verschiedenen Darstellungsformen zur Subtraktion kennengelernt haben.
Hinweis
Das Wichtige bei dieser Unterrichtsaktivität "Minustrio" ist der Herstellungsprozess des Spiels und der Austausch über die verschiedenen Darstellungen: "Was passt warum und warum nicht?" und nicht das Spiel an sich. Deswegen sollten Lehrkräfte insbesondere für die Reflexionsphasen genügend Zeit im Unterricht einräumen.
Bevor mit dem Minustrio gespielt werden kann, muss es hergestellt werden. Hier sehen Sie, wie eine mögliche Reihentransparenz zur Aktivität "Minustrio" im Unterricht aussehen könnte:
Alle Materialien zu dieser Unterrichtsreihe finden Sie im
Materialteil.
1. Einheit: Vorbereitungen für die Spielherstellung Minustrio

Ziele
-
Aktivierung der Vorkenntnisse der Kinder zur Subtraktion und den damit verbundenen Darstellungsformen
-
Schaffung von Transparenz über das Spiel Minustrio für die Kinder durch das Kennenlernen der Minustrio-Spielkarten
Zeit
Darum geht es
Die Kinder erzählen, was sie auf den gezeigten Demo-Spielkarten sehen. Dabei werden die Kinder dazu angeregt, eine erste Sortierung der Spielkarten vorzunehmen in "Rechenaufgaben", "Zwanzigerfeld" und "selbstgemaltes Bild".

Mit den Kindern wird thematisiert, was ein "Trio" ist. Durch Beispiele werden die Kinder zu Überlegungen aufgefordert: "Kann das stimmen?" und "Warum passen diese Karten zusammen?".
Gemeinsam mit den Kindern wird erarbeitet, wie die Spielkarten gemalt werden müssen, damit sie zusammenpassen und wie ein selbstgemaltes Bild aussehen sollte, damit alle Kinder gut und schnell die Minusaufgabe darin erkennen können. Dabei können folgende Kriterien für ein selbstgemaltes Bild vereinbart werden:
-
einfache Dinge in bunt malen (Ich muss erkennen können, was es sein soll.)
-
gut und schnell erkennbare Sortierung der Dinge (Ich mus erkennen können, wie viele Dinge dort sind.)
-
eindeutige Situation malen (Ich muss erkennen können, was passiert ist.)
Dabei können die anderen Darstellungsformen gut einbebunden werden, wie die Handlung durch das gemeinsame Nachspielen von Minussituationen und die Sprache durch das Ausdenken von Rechengeschichten zu einer Minusaufgabe.
Mögliche Knackpunkte
Deuten des Zwanzigerfeldes
Bildliche Darstellungen von didaktischen Materialien stellen einen eigenen Lernstoff dar und unterliegen Konventionen (Vereinbarungen), die erlernt werden müssen.
Werden die Konventionen bildlicher Darstellungsweisen am strukturierten Material im Unterricht nicht genügend behandelt, können Kinder die "durchgestrichenen" Plättchen nicht als "weggenommene" Plättchen deuten, sondern sehen womöglich ein "Halbieren" der Plättchen.
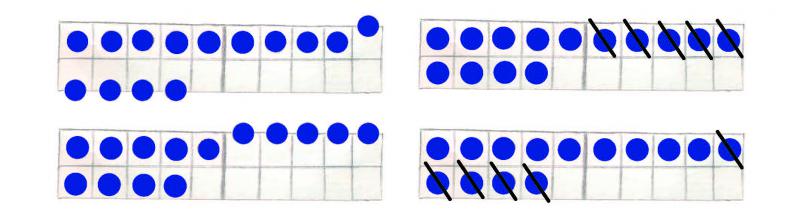 (angelehnt an Häsel-Weide 2014)
(angelehnt an Häsel-Weide 2014)
Am besten werden die später auch im Schulbuch abgebildeten Vereinbarungen für didaktisch bildliche Darstellungen der Subtraktion erörtert.
In der nebenstehenden Abbildung sind verschiedene Darstellungsweisen am Zwanzigerfeld aufgezeigt.
Mehrdeutigkeit von selbstgemalten Bildern
Bilder können mehrdeutig interpretiert werden. Kinder sehen oftmals andere Aufgaben in Bildsituationen hinein, als von dem "Autor" angedacht war. Doch die Kinder müssen die selbstgemalten Bilder der anderen Kinder deuten können.
Deswegen ist es wichtig, dass die Kinder im gemeinsamen Austausch reflektieren, dass es nicht darauf ankommt, dass das Bild möglichst bunt und schön gezeichnet ist, sondern dass der Anfangszustand und die Veränderung für alle Kinder gut und schnell erkennbar sind.

Eine Hilfestellung kann das gemeinsame Erstellen von Drei-Bildergeschichten sein, wie beispielsweise die in der linken Abbildung dargestellten Parksituation mit Autos. Dabei kann gut besprochen werden, in welchem dieser drei Bilder alle Informationen "hineingesehen" werden können (hier das mittlere Bild).
Tipp
Schneiden Sie aus alten (Mathematik-)Büchern Bildgeschichten heraus und kleben Sie diese auf Karteikarten. Auf die Rückseite können Sie die dazugehörige Aufgabe (Lösung) notieren. Die Kinder können sich nun in Partnerarbeit gegenseitig Geschichten zu den Bildern erzählen. Anschließend kann die Kartei ins Matheregal gestellt und in freien Arbeitsphasen genutzt werden.
Die Kinder sollten in der folgenden Situation im Video Spielkarten finden, die zusammenpassen. Hier sehen Sie eine mögliche Erklärung zur Frage: Warum passen die Spielkarten zusammen?

An dieser Situation im Video lässt sich das Potenzial der Unterrichtsaktivität Minustrio gut erkennen. Es ergeben sich vielerlei Gesprächsanlässe.
Ein Kind erklärt zunächst, warum die Karten Rechenaufgabe und Bild zusammenpassen. Dabei bezieht sich das Kind auf die gesamte Aufgabe. Dann entdecken die Kinder, dass nicht nur zwei, sondern sogar drei Karten (zusätzlich die Karte Zwanzigerfeld) zusammenpassen.
Sie begründen die Zusammengehörigkeit in dieser Situation mit den gleichen Anzahlen auf den jeweiligen Spielkarten. Jedoch lässt sich die Erklärung durch das gleiche Ergebnis so nicht auf alle Spielkarten übertragen. Um den Bezug wieder zurück zur gesamten Aufgabe zu erhalten, könnten die Kinder in der Situation beispielsweise gefragt werden, ob auch die Karte mit der Rechenaufgabe 7-4 zu allen anderen Karten passen würde.
2. Einheit: Herstellung des Spiels Minustrio

Ziele
-
Förderung des Darstellungswechsels zwischen Mathesprache und Bildern
-
Austausch über selbsterstellte Spielkarten in Mathe-Konferenzen: "Warum passen die Spielkarten zusammen?"
Zeit
Darum geht es
Die Kinder erhalten pro Kartensatz jeweils drei Karten, die zusammen ein "Minustrio" ergeben.
Eine Hilfestellung für die Kinder ist das vorherige, gemeinsame Sammeln von Ideen für selbstgemalte Bilder, etwa über einen Materialtisch und auch über die gemeinsame Besprechung von den Demo-Spielkarten, die anschließend an die Tafel oder auf ein Plakat gehängt werden können.

Die Kinder können sich dann während der Herstellung eigener Minustrio-Spielkarten von dort Anregungen holen.
Durch Beobachtungen während des Herstellens der Spielkarten können Lehrkräfte herausfinden, bei welchem Darstellungswechsel Kinder noch größere Schwierigkeiten haben und diese durch gezielte Reflexionsgespräche über die selbsterstellten Karten thematisieren.
Nach Herstellung einiger Spielkarten tauschen sich die Kinder in Mathekonferenzen über ihre erstellten Spielkarten aus, überprüfen diese auf die vorher besprochenen Kriterien zum Malen selbstgemalter Bilder zur Subtraktion und geben sich gegenseitig Tipps zur Verbesserung.
Zuletzt sollte die Lehrperson die Spielkarten kontrollieren und die Kinder auf Verbesserungen hinweisen.
Differenzierungsmöglichkeit
Die Lehrperson kann unterschiedliche Zahlenräume der Rechenaufgaben zur Differenzierung nutzen und später auch Blanko-Rechenaufgaben zum eigenen Erfinden zur Verfügung stellen. Die Kinder können selbst auswählen und entscheiden, wie viele "Trio"-Kartensätze sie selbst gestalten.
3. Einheit: Spielideen

Ziele
-
Förderung des Darstellungswechsels zwischen Mathesprache, Bildern und Sprache
-
Gesprächsanlässe anregen: "Warum passen die Spielkarten zusammen?"
Zeit
Darum geht es
Für das Spiel werden einige erstellte Minustrio-Spielkarten der Kinder ausgesucht und die für das Spiel verwendeten Minusaufgaben werden auf kleinen Zetteln notiert. Empfehlenswert sind neun Minustrio-Kartensätze pro Sechser-Gruppentisch. Die Kinder können so auch bei der vorherigen Auswahl eingebunden werden.

Die Kinder spielen bei diesem Spiel in Zweierteams zusammen. Jedes Zweierteam erhält zufällig neun Spielkarten aus dem zuvor gemischten Kartenstapel und verteilt diese auf ihrem vor sich liegenden Bingo-Feld.
Die Lehrperson (später ein Kind) zieht eine notierte Minusaufgabe und liest diese den Kindern laut vor.
Alle Zweierteams dürfen genau eine Spielkarte umdrehen, die zu der genannten Minusaufgabe passt.
Das Zweierteam, das als erstes in seinem Bingo-Feld drei Spielkarten untereinander oder nebeneinander umdrehen konnte, hat gewonnen.
Hinweis
Zur Überprüfung müssen die Kinder die Spielkarte, die sie umdrehen möchten, zuvor hochhalten und den anderen Kindern zeigen. Dabei können Gesprächsanlässe (auch nur zwischen den einzelnen Spielpartnern) entstehen und Impulse durch die Lehrperson hereingegeben werden, wie beispielsweise "Was hast du besonders schnell erkannt? Woran? Warum?...“.
Weitere Spielideen mit den selbst erstellten Minustrio-Spielkarten finden Sie im Materialteil.
Das Minustrio kann den Kindern in freien Arbeitsphasen zur Verfügung gestellt werden, immer mit der Aufgabe, gemeinsam eine weitere Spielidee auszuprobieren oder sogar zu entwickeln. Dadurch beschäftigen sich die Kinder intensiv mit den einzelnen Karten und wechseln schließlich "geläufiger" zwischen den verschiedenen Darstellungsformen.
Wichtig ist also, dass nicht das Spiel als Produkt im Vordergrund steht, sondern der Herstellungsprozess und die dadurch entstehenden Reflexionsphasen im Unterricht über die Diskussion "passender" Darstellungen.
Denn für ein umfassendes Operationsverständnis sind vielfältige Darstellungswechsel und damit immer wieder Rückbezüge und Vergleiche verschiedener Darstellungsformen von großer Bedeutsamkeit.