Unterricht

Kombinatorische Denk- und Arbeitsweisen entwickeln

An dieser Stelle wird ein Beispiel aufgegriffen, das variiert und in unterschiedlichen Klassenstufen bearbeitet werden kann. Es ermöglicht unterschiedliche Zugänge (enaktiv, ikonisch und symbolisch)  und bietet die Chance, entwickelte Lösungsstrategien auf analoge, in andere inhaltliche Kontexte eingebettete Aufgaben zu übertragen. Das zum Einstieg genutzte Problem ist die Umkehrung der im folgenden aufgeführten Aufgabenstellung.

Diese Aufgabe kann bereits von Kinder des ersten Schulbesuchsjahres handelnd gelöst werden: Wir geben uns die Hand und zählen. Dabei muss aufgepasst werden, wer wem schon die Hand geschüttelt hat. In einer Lerngruppe ( 4 Kinder) wurde festgelegt, dass Lisa mit dem Händeschütteln beginnen soll. Sie schüttelte den 3 anderen Kindern die Hand. Das zweite Kind dann noch den 2 anderen. Jan muss zum Schluss feststellen, dass er ja allen schon die Hand gegeben hat, also kein weiterer, neuer Handschlag mehr hinzukommt.  Insgesamt gibt es also 3+2+1= 6 Handschläge.

Kinder einer anderen 4-er Gruppe dokumentierten ihre Überlegungen in einer zeichnerischen Darstellung. Alle Namen wurden verteilt und das Handschütteln durch Verbindungsstriche veranschaulicht. Es wird erkannt, dass z. B. der Handschlag Anna-Tom identisch ist mit dem Handschalg Tom-Anna. Er wird nur einmal gezählt.

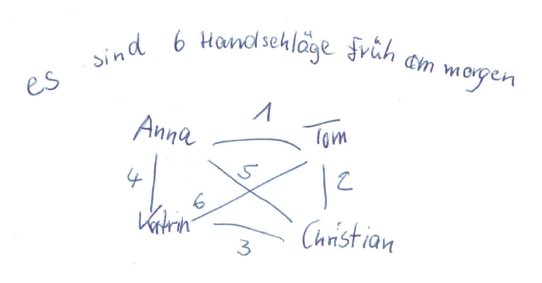
Die Aufgabe kann variiert werden, indem zugelassen wird, dass die Aufgabe für die in der Realität möglicherweise vorhandenen unterschiedlich großen Gruppentische bearbeitet wird.

Auch die Kinder selbst variieren Aufgabenstellungen. So haben die Kinder, die für ihren 5er-Tisch die Anzahl der Händedrücke ermittelt haben (10), dann überlegt, wie oft wohl bei 12 Kindern die Hände geschüttelt werden. Der Punkt, manchmal war auch ein Doppelpunkt zu finden, ist kein Operationszeichen, sondern ein Zeichen, nach dem die Anzahl der Händedrücke des jeweiligen Kindes notiert werden.

Interessant sind immer wieder zeichnerische Lösungen der Kinder. In diesem Fall hat (anscheinend) schon das Aufzeichnen der 8 Gäste, ohne die Verbindungslinien, ausgereicht, um die Lösungsschritte zu erkennen und anderweitig zu dokumentieren.

Im Reflexionsprozess zu dieser Aufgabe kann bzw. sollte die Chance genutzt werden, die Analogie zur folgenden Aufgabe herauszuarbeiten: Die Anzahl der Verbindungslinien zwische 8 Punkten, von denen keine drei Punkte auf einer Geradenden liegen.

Kinder können ihr Vorgehen auf analoge Aufgabenstellungen, wie das Anstoßen mit Gläsern, übertragen. Die folgenden Abbildungen zeigen Kinderdokumente.

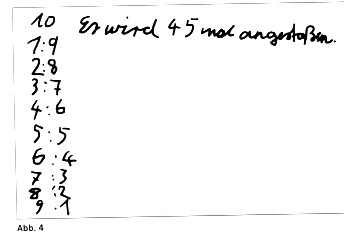
Die Summe der aufgeführten Zahlen haben die Kinder (zu Beginn der Klasse 3) genauso korrekt ermittelt, wie die Gruppe der Kinder, die herausgefunden hat, dass bei 10 Personen 45 mal die Gläser klingen, wenn jeder mit jedem anstößt. Die Notation 1:9 bedeutet hier, der erste stößt mit 9 weiteren an.

An dieser Stelle wollen wir nun endlich das Beispiel der Einstiegsseite aufgreifen.

Es ist eine Umkehrungen der bisherigen kombinatorischen Aufgabenstellungen. Derartige Aufgaben sind ganz besondere Herausforderungen. Sie sind insbesondere geeignet, mathematisch begabten Grundschulkindern zu fordern und zu fördern. An dieser Stelle eine Kinderlösung. Versuchen Sie zunächst, den Lösungsweg nachzuvollziehen und zu interpretieren?

Das Kind hat überlegt, dass die beiden neuen Gäste mit den anderen anstoßen, insgesamt beide zusammen 33 mal. Da es zwei Gäste sind, wurde die Hälfte gebildet: 16 1/2., d. h.  einer mit 16 und der andere mit 17 Gästen, was zu der korrekten Lösung führt.
Eine andere günstige Überlegung, die Kinder beschrieben: 33 muss als Summe von zwei aufeinanderfolgenden natürlichen Zahlen dargestellt werden, was ebenso zu  16+17 führt.

Die bisherigen Schülerdokumente zeigen, dass Kinder unterschiedliche Darstellungen nutzen, um ihre Überlegungen sichtbar werden zu lassen. Diese Darstellungen zeigen auch, dass Kinder die Informationen des Kontextes mathematisieren. Diese Aufgaben sind somit auch geeignet, mathematisches Modellieren bei den Kindern zu schulen. Derartige Aufgaben regen Kinder an, sich im Lösungsprozess auszutauschen, d.h. sie kommunizieren und argumentieren bereits im Arbeitsprozess. Darüber hinaus bieten die Lösungen zu Variationen dieser Aufgaben vielfältige Möglichkeiten, um die Kinder anzuregen, Lösungen zu vergleichen, nach Strukturen und Muster zu suchen und diese zu beschreiben. Insbesondere das Herausstellen von Analogien unterstützt das Erkennen und die Entwicklung tragfähiger Lösungsstrategien.

In den auf der Material-Seite aufgeführten Zeitschriften-Beiträgen finden Sie eine Vielzahl weiterer Anregungen für kombinatorische Aufgabenstellungen.
Anregungen, Aufgaben (u.a. Spielansetzungen für ein Fußballturnier) und Beispiel für Lösungsstrategien finden Sie auch auf den Seiten des Partnerprojektes KIRA: Daten, Häufigkeiten und Wahrscheinlichkeiten – Kombinatorik.