Überschlagsstrategien entwickeln und sinnvoll einsetzen
Nun wird dargestellt, wie den Kindern im Unterricht nahe gebracht werden kann, wozu und wann eine Überschlagsrechnung sinnvoll gebraucht werden kann. Aus den auf der vorherigen Seite dargelegten Hintergründen zum Überschlagsrechnen ergeben sich drei Aspekte, die im Unterricht Berücksichtigung finden sollten.
Grundsätzlich lohnt es sich dem Überschlagsrechnen eine (oder mehrere) Unterrichtsreihen zu widmen. Eine mögliche Unterrichtsreihe zum Überschlagsrechnen, die diese drei genannten Aspekte berücksichtigt, wird im Folgenden am Beispiel der Addition vorgestellt. Die Aufgabenbeispiele sind dem Material von „Mathe sicher können“ (Voßmeier & Selter 2017, S. 30 ff.) entnommen.
Zu Beginn der Unterrichtsreihe wird den Kinder im Plenum Tims Problem vorgestellt (siehe Abb. 1): "Warum findet Tim die Aufgabe schwierig? Was meint Tim damit ungefähr?!!

Nach einer ersten Ideensammlung erhalten die Kinder den Auftrag leichtere Aufgaben – eine Überschlagsrechnung – zu finden, um so zu erfahren, dass es beim Überschlagsrechnen vor allem um die Vereinfachung einer sonst schwierig (im Kopf) zu lösenden Rechnung geht.
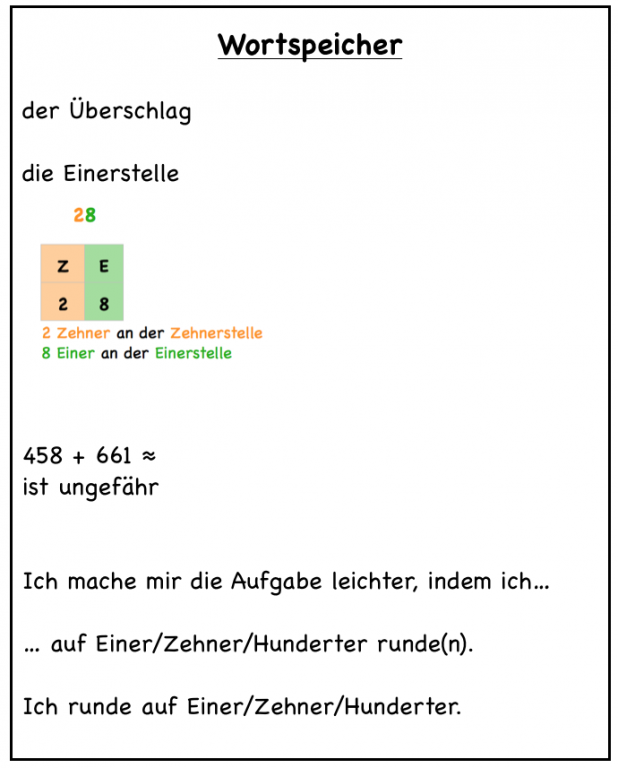
Bevor die Kinder in Einzel- oder Partnerarbeit selbst Überschlagsrechnungen zu Tims und weiteren Rechenaufgaben suchen, werden im Plenum erste Beispiele für mögliche Vereinfachungen gesammelt. Bei Bedarf können hier die Beispiele aus der Aufgabe b) (Abb. 2) herangezogen werden. Diese können vor allem zur Einführung der notwendigen Fachsprache genutzt werden (vgl. auch Abb. 4). Die Lehrkraft fordert dazu immer wieder eine Beschreibung der Vereinfachung von den Kindern ein, wie z.B.: „Ich mache mir die Aufgabe leichter, indem ich auf Zehner runde.“

Anschließend ordnen die Kinder in Partnerarbeit Kärtchen mit vorgegebenen Überschlagsrechnungen zur Aufgabe 458 + 661 den Strategien der Kinder in b) zu (Abb. 3). Die Strategien (1), (2) und (4) entsprechen dem Runden. (3) und (4) stehen für das Abbruchverfahren. Auch wenn die Vereinfachung hier aussieht wie die Anwendung der konventionellen Rundungsregeln, so werden diese an keiner Stelle erwähnt. Vielmehr geht es hier um die Idee, dass das Kind mit den glatten Zehnerzahlen leichter rechnen kann als mit den genauen Zahlen.

Wichtiger Bestandteil dieser Einheit ist die abschließende Reflexion. Dabei sollten die Besonderheiten der einzelnen Strategien thematisiert werden. Die Rundungsregeln als solche spielen dabei keine Rolle, da diese sonst leicht von den Lernenden als unverstandenes Rezept genutzt werden. Vielmehr sollten die folgenden Fragen im Vordergrund stehen: „Warum passt diese Überschlagsrechnung zu der Aufgabe? Und warum ist die Überschlagsrechnung (hier) für dich einfacher zu rechnen?“
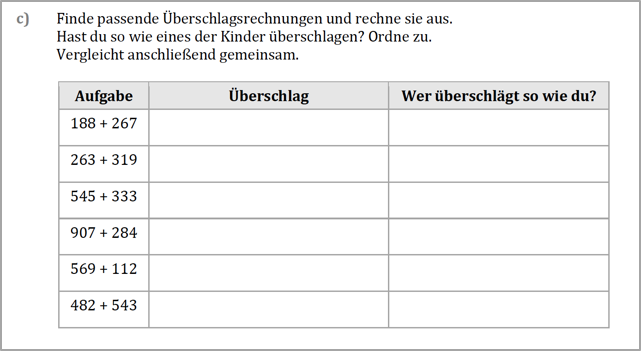
In der/den folgende(n) Unterrichtsstunde(n) können die Kinder dann selbständig zu weiteren Aufgaben passende Überschläge finden: „Rechne wie...“ (siehe Abb. 5). Auch hier sollten die jeweils genutzten Strategien analog zu den in b) aufgeführten Kinderlösungen benannt werden (z.B. „Tara - Ich lasse die Einerstelle weg“). Auch hier stehen immer wieder die Idee der Vereinfachung und zunehmend auch Schnelligkeit im Vordergrund.

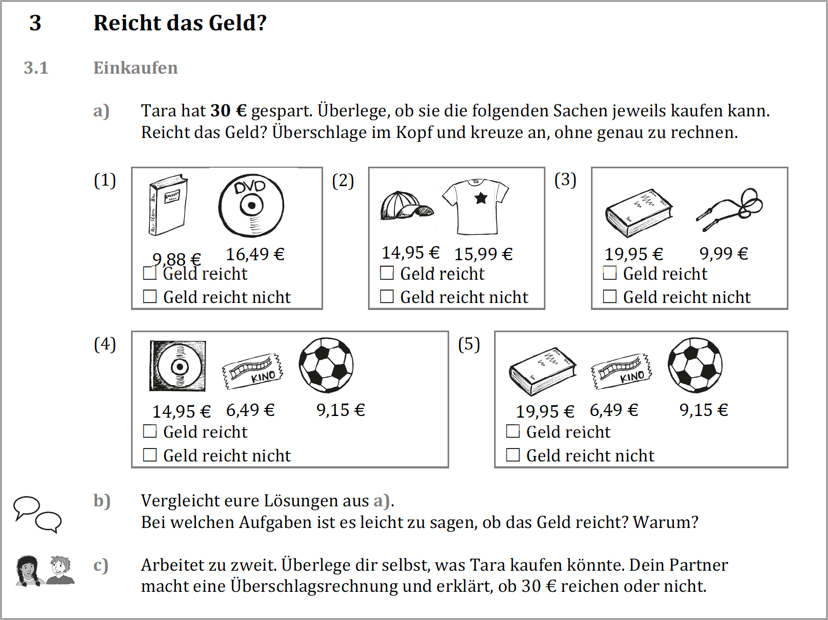
Nach der Einführung verschiedener Überschlagsstrategien, wird der Zusammenhang bzw. die Unterschiede zwischen einer Überschlagsrechnung und der dazugehörigen genauen Rechnung näher in den Blick genommen. Dazu können die vorab erwähnten indirekten Überschlagsfragen „Kann das stimmen?“ und „Reicht das Geld?“ eingesetzt werden (Abb. 7 und 8).
Die Art der Fragestellung führt dazu, dass die Antwort keine Zahl erfordert. Vielmehr muss mathematisch begründet werden, warum das Geld reicht oder nicht. Wird eine der bisher erarbeiteten Strategien zum Überschlagen angewendet, müssen die Kinder lernen, wie sie mit solch einem Überschlagsergebnis umgehen müssen, um eine korrekte Antwort auf die Frage zu erhalten.
So muss beachtet werden, ob der Überschlag über oder unter dem genauen Ergebnis liegt. Dazu muss man wissen, ob man auf- oder abgerundet und wie sich dies auf das Ergebnis ausgewirkt hat. Dies fällt vielen Kindern noch schwer. Hier geht es also auch darum, ein gewisses Gespür für Zahlen zu entwickeln bzw. anzuwenden, aber auch seine Argumentation auszudrücken. Wie solch eine Begründung aussehen kann, zeigt das Beispiel von Lennard in Abb. 6.

Besonders fruchtbare Gesprächsanlässe bieten „Reicht das Geld?“-Aufgaben, bei denen der Überschlag zu einem Betrag über dem vorhandenen Budget liegt, das genaue Ergebnis aber darunter, wie im nachstehenden Beispiel (Abb. 9).
Jana hat 80€. Sie möchte sich drei Hosen zu je 26€ kaufen. Reicht das Geld?

Nicht selten schließen Kinder in Fällen wie diesen direkt aus dem Überschlagsergebnis dass das Geld nicht reiche. An dieser Stelle ist es deshalb wichtig die Frage zu stellen: „Wann könnte das Geld reichen?“ und somit gezielt die Auswirkungen des Rundens in Betracht zu ziehen. Jana hat für ihren Überschlag dreimal aufgerundet. Deshalb muss das genaue Ergebnis auf jeden Fall kleiner sein als das Überschlagsergebnis (90€). Betrachtet man die Auswirkungen genauer, so kann man ausrechnen, dass das genaue Ergebnis um 3 · 4€ , also 12€ kleiner ist als 90 €. Das Geld reicht also doch.
Wie beurteile ich, wann ein Überschlag sinnvoll ist?
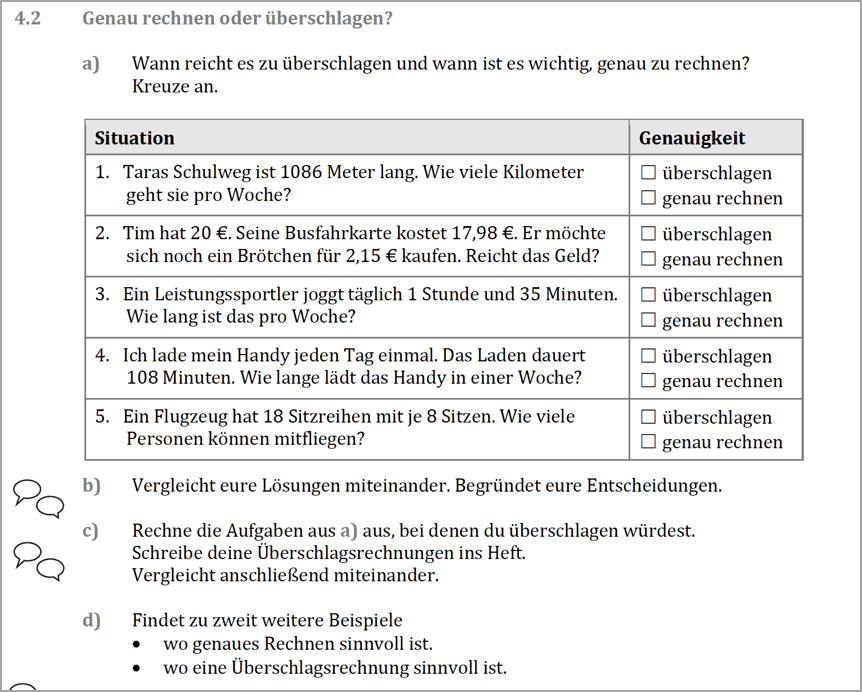
Zum Abschluss der Unterrichtsreihe bietet es sich an, das Thema Genauigkeit näher zu beleuchten. Dazu eignen sich Aufgaben, bei denen die Kinder begründen sollen, ob ein Überschlag ausreicht oder ob eine genaue Rechnung notwendig ist (vgl. Abb. 10). An dieser Stelle spielt die Kommunikation im Unterricht eine große Rolle, denn bei diesem Thema können die Meinungen durchaus auseinandergehen.
Es ist vor allem wichtig, dass die Kinder ihre Meinungen austauschen und mathematisch fundiert begründen. So wäre für die 3. Situation (Abb. 10) folgende Standpunkte denkbar:
Will der Leistungssportler z.B. seine Trainingszeit erhöhen, muss man sicherlich genauer rechnen. Oder joggt er immer seine feste Runde, für die er ungefähr 1Stunde und 35 Minuten benötigt und möchte dies auf eine Woche hochrechnen - dann ist eine Überschlagsrechnung völlig ausreichend.
Wie kann es weitergehen?
Wichtig ist, dass das ungefähre Rechnen nicht nur in separaten Unterrichtsreihen gewürdigt wird, sondern fortlaufend im Mathematikunterricht seinen Platz hat. Gerade beim Sachrechnen sollte daher immer wieder – analog zur Aufgabe 4.2 – diskutiert werden, ob ein Überschlag ausreicht oder ob eine genaue Rechnung notwendig ist. Dazu eignen sich insbesondere auch Schätz- und Fermi-Aufgaben (KIRA: Größen und Messen – Bauernhofaufgaben) sowie Alltagssituationen.